
- •Занятие 6 Вторичная обработка радиолокационной информации
- •Существо процедур вторичной обработки рли
- •Стробирование и селекция отметок в стробах
- •1 Оценка параметров траекторий Сглаживание и экстраполяция при вторичной обработке
- •Алгоритм фильтрации параметров траектории по методу максимального правдоподобия
- •Оптимальное последовательное сглаживание координаты и скорости ее изменения
- •Последовательное сглаживание скорости и курса. Выявления маневра воздушного объекта
- •2 Обнаружение и сопровождение траекторий воздушных объектов в обзорной рлс
- •Структурная схема алгоритма обнаружения траекторий
- •Структурная схема алгоритма сопровождения траекторий
- •Полуавтоматическое сопровождение траекторий воздушных объектов
Стробирование и селекция отметок в стробах
Одной из операций, выполняемых в процессе сопровождения целей, является выделение области, в которой с определенной вероятностью ожидается появление отметки в новом обзоре (стробирование).
Строб представляет собой заранее выбранную область зоны обзора РЛС, координаты центра которой совпадают с координатами ЭТ. Размер и форма строба выбираются так, чтобы вероятность попадания в него наблюдаемой отметки, принадлежащей данной трассе была близка к единице.
В строб могут попасть и ложные отметки или отметки, принадлежащие другим траекториям. Поэтому возникает необходимость селекции отметок, попавших в строб, с целью выбора одной отметки, для которой вероятность принадлежности к сопровождаемой трассе является наибольшей. Селекция производится на основе сравнения координат и параметров новых отметок с экстраполированными координатами и характеристиками сопровождаемых трасс.
К числу сравниваемых параметров могут относиться данные о высоте цели, ее составе, признак гос. принадлежности и др. В простейшем случае селекция трасс производится только по координатам отметок.
Стробирование отметок от цели. Стробирование отметок может быть физическим или математическим.
Под физическим стробированием понимают выделение предполагаемой области появления отметки путем непосредственного воздействия на приемное устройство РЛС.
Под математическим стробированием понимается формирование предполагаемой области появления новой отметки в виде некоторой совокупности чисел (границ строба).
Важной задачей в процессе стробирования отметок трассы является выбор формы и размеров стробов.
Для определения оптимальной формы стробов необходимо найти поверхность равновероятного отклонения НО от ЭТ.
Обозначим через Δх, Δу, ΔН суммарные отклонения НО от ЭО в выбранной (прямоугольной) системе координат. Обычно эти составляющие можно считать случайными, статистически независимыми и подчиненными нормальному закону распределения вероятности. Тогда при нулевом математическом ожидании <Δх> = <Δу> = <ΔН> = 0 и дисперсиях σ2х, σ2у, σ2н плотность распределения трех независимых случайных величин Δх, Δу, ΔН будет иметь вид
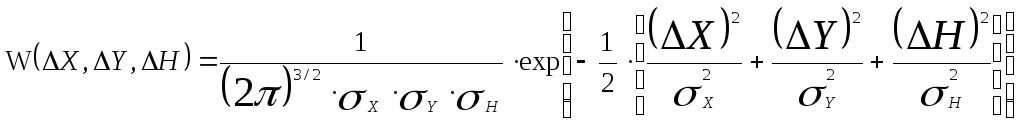
Поверхность, соответствующая одинаковой плотности вероятности определяется уравнением

где d – постоянная величина.
Уравнение (5.25) – уравнение эллипсоида, отнесенного к сопряженным полуосям dσх, dσу, dσн. Поэтому и сам строб должен иметь форму эллипсоида с сопряженными полуосями kσх, kσу, kσн, где k – коэффициент увеличения размеров строба по сравнению с размерами единичного эллипсоида. Вероятность попадания случайной точки в эллипсоид равной вероятности зависит от коэффициента k.
![]()
![]()
При k = 3-3.5 вероятность P(k) близка к 1 (правило «3-х сигма»). Именно такие значения k и необходимо выбирать при формировании эллипсоидального строба. Сформировать эллипсоидальный строб (рис.5.25,а) очень трудно как при физическом, так и при математическом стробировании.
Обычно форма строба выбирается простейшей для задания в той системе координат, в которой осуществляется обработка РЛИ. При обработке в сферической системе координат простейший строб задается линейным размером по дальности ΔДстр и двумя угловыми размерами: по азимуту Δβстр и по углу места Δεстр (рис.5.25,б).
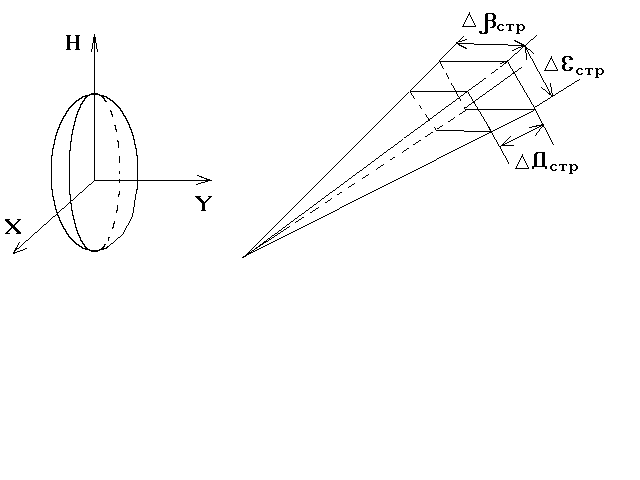
а) б)
Рис.5.25. Эллипсоидальный строб (а) и простейший строб (б)
Эти размеры установлены заранее, исходя из учета максимальных значений случайных и динамических ошибок по всем подлежащим обработке трассам.
В качестве координат центра строба выбираются экстраполированные значения дальности Дnэ, азимута βnэ и угла места εnэ, рассчитанные на n-й обзор. Поэтому очередная отметка с координатами Дn, βn и εn считается попавшей в строб, если одновременно выполняются условия
|Дn – Дnэ| ≤ ΔДстр/2; |βn – βnэ| ≤ Δβстр/2; |εn – εnэ| ≤ Δεстр/2.
При обработке в прямоугольной системе координат x,y,H целесообразно выбрать строб в виде параллелепипеда с параметрами Δхстр, Δустр, ΔНстр. Тогда условия попадания отметки в строб будет определяться неравенствами:
|xn – x*nэ| ≤ Δxстр/2; |yn – y*nэ| ≤ Δyстр/2; |Hn – H*nэ| ≤ ΔHстр/2.
В системах с пороговым обнаружением маневра, (т.е. в системах, в которых принимается только двухальтернативное решение о наличии или отсутствии маневра и не измеряется его интенсивность) возможен дифференцированный подход к выбору стробов. Если маневр цели не обнаруживается, то строб рассчитывается только на компенсацию случайных ошибок. При обнаружении маневра строб рассчитывается на случай наибольшей его интенсивности.
На размеры строба в сильной степени влияют пропуски отметок от цели. При пропуске одной или даже нескольких отметок от цели система сопровождения продолжает трассу по предыдущим данным путем экстраполяции ее координат и параметров. Экстраполированная отметка принимается за истинную до тех пор, пока не будет получена истинная отметка или принято решение о сбросе трассы с сопровождения.
Как показывают расчеты, при пропуске отметок ошибки экстраполяции быстро возрастают, что приводит к необходимости соответствующего увеличения размеров строба. Обычно размеры стробов рассчитываются заранее на случай пропуска одной, двух и т.д. отметок при отсутствии и наличии маневра цели.
При 5-8 пропусках подряд ошибки экстраполяции становятся настолько значительными, что дальнейшее сопровождение по экстраполированным отметкам не имеет смысла. Кроме того, наличие такого числа пропусков может с достаточно большой вероятностью свидетельствовать о выходе цели из зоны обнаружения РЛС. Поэтому при наличии такого числа пропусков принимается решение о сбросе трассы с сопровождения. Это решение отображается на экране ИКО определенным символом.
Селекция отметок в стробе. В строб помимо истинной отметки будут попадать ложные отметки, образованные помехами, прошедшими фильтр первичной обработки. Попадание ложных отметок в строб создает в нем неопределенную ситуацию, требующую дальнейшего анализа.
При анализе возможны два подхода:
1. Имея несколько отметок в стробе, продолжать траекторию по каждой из них, трассы, продолженные по ложным отметкам, из-за отсутствия корреляции между последними в соседних обзорах будут через несколько обзоров сброшены, а трассы, продолженные по истинным отметкам, останутся.
2. Выбрать в стробе одну отметку, вероятность принадлежности которой к сопровождаемой трассе наибольшая, и по ней продолжать трассу, а остальные отметки отбросить как ложные.
На практике используют второй подход, т.к. он требует меньше оборудования и быстродействия ЦВМ и уменьшает число ложных трасс.
Оптимизация процесса селекции отметок по их отклонениям от центра строба производится по критерию максимального правдоподобия, в соответствии с которым за истинную отметку надо принимать ту, для которой функция правдоподобия максимальна.
Для случая селекции в трехмерном стробе, грани которого параллельны главным полуосям эллипсоида суммарных ошибок, условие максимального правдоподобия записывается в виде:
W(Δхi*, Δуi*, ΔНi*) = max {W(Δхi, Δуi, ΔНi)}, (5.26)
где i* – номер отметки, принятой за истинную.
Очевидно i-ой отметке будет соответствовать свое значение параметра di
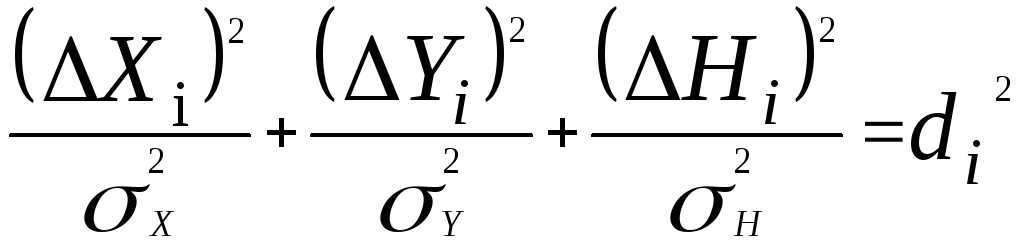
характеризующего относительные размеры эллипсоида (по сравнению с единичным).
С учетом выражения для di функция правдоподобия для i-ой отметки будет равна
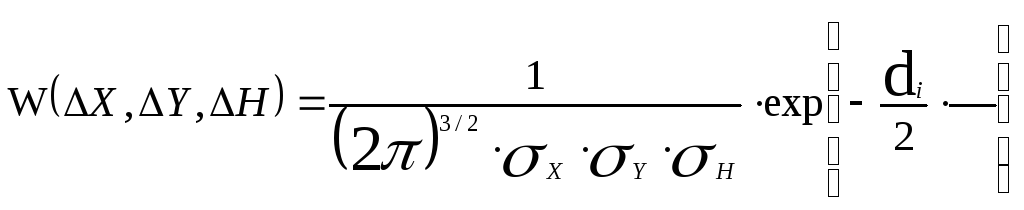
Откуда следует, что условие (5.26) эквивалентно условию
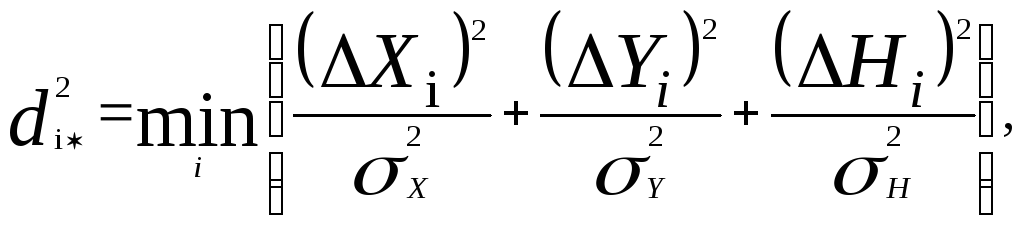
где i* имеет тот же смысл.
Таким образом, в качестве отметки для продолжения трассы надо брать ту, эллипсоидальное отклонение которой от центра строба минимально. В двумерном стробе оптимальная селекция отметок должна осуществляться по минимуму эллиптических отклонений.
При выборе эллиптического (эллипсоидального) строба и селекции отметок по минимуму эллиптических (эллипсоидальных) отклонений от центра строба обеспечивается высокая надежность сопровождения цели без сбоев, однако для своей реализации этот метод требует большого объема вычислений. Поэтому на практике используют более простые методы селекции.
Естественным упрощением рассмотренного оптимального алгоритма является алгоритм селекции по минимуму суммы квадратов линейных отклонений координат отметки от центра строба. Это соответствует предположению о шаровом распределении суммарных ошибок, т.е. σ2х = σ2у = σ2н.
При обработке в сферической системе координат упрощенный алгоритм селекции записывается в виде
d2i* = min{(Δхi)2 + (Δуi)2 + (ΔНi)2},
где i* – номер отметки принятой за истинную.
В двумерном случае алгоритм селекции осуществляется по минимуму линейных отклонений
ρ2i* = min{(Δхi)2 + (Δуi)2}.
Очевидно, надежность сопровождения цели при упрощении алгоритма селекции отметок в стробе снижается. Для повышения надежности сопровождения предусматривается возможность ввода корректур (поправок) оператором в случае выхода истинной отметки из строба сопровождения.
В двумерном стробе оптимальная селекция отметок должна осуществляться по минимуму эллиптических отклонений. Для пояснения сказанного рассмотрим пример. Пусть вблизи ЭТ имеется две текущие отметки «а» и «б», полученные по данным РЛС кругового обзора (рис.5.26). Поскольку линейные ошибки местоположения цели РЛС по координатам Д и β, как правило неодинаковы (σβлин> > σд), то расстояние отметок относительно ЭТ будет характеризоваться эллипсом рассеяния с сопряженными полуосями σβлин и σд.
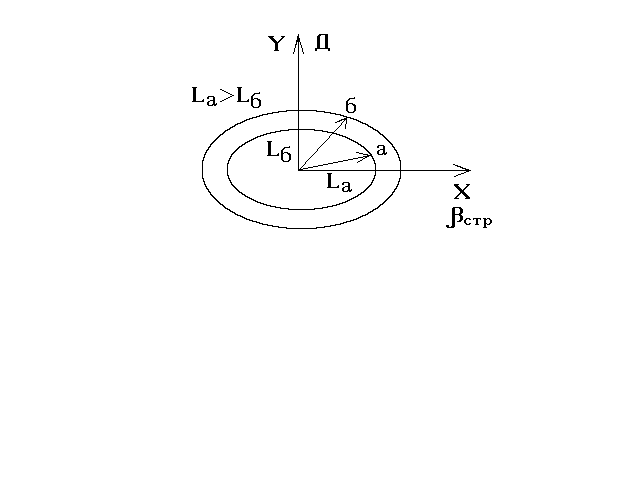
Рис.5.26
Проведем через точки «а» и «б» эллипсы равной вероятности. Как видно из рисунка, отметка «а» лежит на эллипсе с меньшим отклонением, чем отметка «б», т.е. параметр dа < dб. Следовательно, отметка «а» и должна быть выбрана в качестве истинной. Между тем, если сравнить линейное отклонение отметок «а» и «б» от ЭО, то окажется, что lа > lб.
