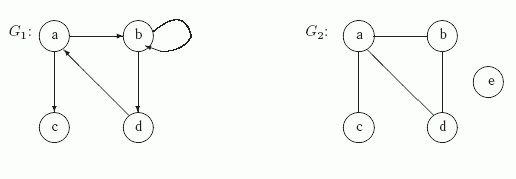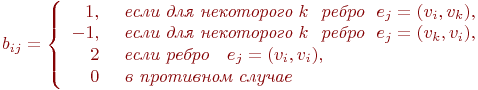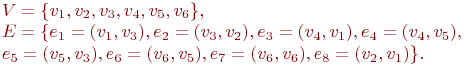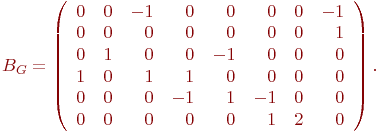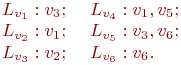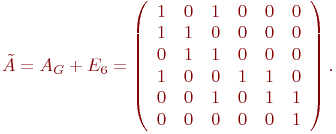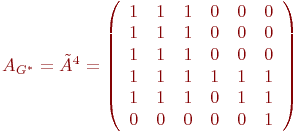Дискретная математика

9. Лекция: Графы: представления, достижимость и связность: версия для печати и PDA  Ориентированные и неориентированные графы. Представление графа с помощью матрицы смежности, матрицы инцидентности и списов смежности. Граф достижимости (транзитивного замыкания). Отношение взаимной достижимости, компоненты сильной связности и базы ориентированного графа

Основные понятия

Мы часто сталкиваемся с задачами, в условиях которых заданы некоторые объекты и между некоторыми их парами имеются определенные связи. Если объекты изобразить точками (вершинам и), а связи - линиями ( ребрами ), соединяющими соответствующие пары точек, то получится рисунок, называемый графом. Историю теории графов принято исчислять с 1736 г., когда Эйлер исследовал "задачу о кенигсберских мостах": построить в графе циклический путь, проходящий по одному разу через каждое ребро. В середине 19-го века Гамильтон заинтересовался задачей построения циклического пути, проходящего по одному разу через каждую вершину графа¹⁾ К тому же времени относится использование графов для анализа электрических цепей ( Кирхгоф ) и химических молекул (Кэли). Развитие современной теории графов относится к 30-м годам 20-го столетия. Они нашли многочисленные применения в электротехнике, электронике, биологии, экономике, программировании и в других областях. В этой и двух следующих лекциях мы рассмотрим основные понятия теории графов и несколько широко используемых в различных приложениях типовых задач, таких, как представления графов, отношение достижимости и транзитивное замыкание графа, компоненты сильной связности ориентированного графа и его базы, деревья и их обходы, минимальные остовные деревья, поиск в глубину и поиск кратчайших путей. Основное внимание уделено алгоритмическим процедурам, решающим указанные задачи.

Приведем основные определения.

Определение 9.1. Ориентированный граф - это пара (V, E), где V - конечное множество вершин (узлов, точек) графа, а E - некоторое множество пар вершин, т.е. подмножество множества V x V или бинарное отношение на V. Элементы E называют ребрами (дугами, стрелками, связями). Для ребра  вершина u называется началом e, а вершина v - концом e, говорят, что ребро e ведет из u в v.

Неориентированный граф G=(V, E) - это ориентированный граф, у которого для каждого ребра  имеется противоположное ребро , т.е. отношение Eсимметрично. Такая пара (u,v), (v,u) называется неориентированным ребром. Для его задания можно использовать обозначение для множества концов: {u, v}, но чаще используется указание одной из пар в круглых скобках. Если , то вершины u и v называются смежными в G, а ребро e и эти вершины называются инцидентными. Степенью вершины внеориентированном графе называется число смежных с ней вершин. Вершина степени 0 называется изолированной.

В ориентированном графе полустепень исхода вершины - это число исходящих из нее ребер, а полустепень захода - это число входящих в данную вершину ребер.

Заметим, что в ориентированном графе может быть ребро вида (u,u), называемое петлей, а в неориентированном петель не бывает.

Пример 9.2. На рис.9.1 приведены примеры ориентированного графа G₁=(V₁, E₁) и не ориентированного графа G₂=(V₂, E₂). Здесь V₁={ a,b,c,d}, E₁={ (a,b), (a,c), (b,b), (b,d), (d,a)}, V₂={ a,b,c,d}, E₂={ (a,b), (a,c), (a,d), (b,d)}. В графе G₁ ребро (b,b) является петлей, полустепень исхода вершины a равна 2, а полустепень захода для нее равна 1. Вграфе G₂ степень вершины a равна 3, вершин b и d - 2, вершины c - 1, а вершины e - 0, т.е. вершина e является изолированной,

Рис. 9.1.  Ориентированный граф G1 и неориентированный граф G2

Во многих приложениях с вершинам и и ребрами графов связывается некоторая дополнительная информация. Обычно она представляется с помощью функций разметки вершин и ребер.

Определение 9.2. Размеченный граф - это ориентированный или неориентированный граф G= (V, E), снабженный одной или двумя функциями разметки вида: l: V -> M и c: E -> L, где M и L - множества меток вершин и ребер, соответственно.

Упорядоченный граф - это размеченный граф G= (V, E), в котором ребра, выходящие из каждой вершины , упорядочены, т.е. помечены номерами 1, ..., k_v, где k_v - полустепень исхода v, т.е. .

В качестве множества меток ребер L часто выступают числа, задающие "веса", "длины", "стоимости" ребер. Графы с такой разметкой часто называют взвешенными.

Во многих случаях естественно не различать графы, отличающиеся лишь именами (порядком) вершин.

Определение 9.3. Изоморфизм графов. Два графа G₁= (V₁, E₁) и G₂= (V₂, E₂) называются изоморфными, если между их вершинам и существует взаимно однозначное соответствие  такое, что для любой пары вершин u, v из V₁ ребро  ребро .

Для изоморфизма размеченных графов требуется также совпадение меток соответствующих вершин :  и/или ребер: .

Многие приложения графов связаны с изучением путей между их вершинами.

Определение 9.4. Путь в ориентированном или неориентированном графе - это последовательность ребер вида (v₁,v₂),(v₂,v₃), ... , (v_n-1,v_n). Этот путь ведет из начальнойвершины v₁ в конечную вершину v_n и имеет длину n-1. В этом случае будем говорить, что v_n достижима из v₁. Будем считать, что каждая вершина достижима сама из себя путем длины 0. Путь можно также определять как соответствующую последовательность вершин: (v₁,v₂,v₃, ... , v_n-1,v_n), где  при i=1,2,..., n-1.

Путь назывется простым, если все ребра и все вершины на нем, кроме, быть может, первой и последней, различны.

Циклом в ориентированном графе называется путь, в котором начальная вершина совпадает с конечной и который содержит хотя бы одно ребро. Цикл (v₁,v₂, ... , v_{n-1},v_n=v₁)называется простым, если в нем нет одинаковых вершин, кроме первой и последней, т.е. если все вершины v₂, ... , v_{n-1} различны.

В неориентированном графе путь (v₁,v₂, ... , v_n-1,v_n=v₁) называется циклом, если n >= 4 и все ребра (v_i, v_i+1) различны.

Если в графе нет циклов, то он называется ациклическим.

Из последнего определения следует, что длина цикла в неориентированном графе не меньше 3. Следующее утверждение непосредственно следует из определений.

Лемма 9.1. Если в графе G ( ориентированном или неориентированном ) имеется путь из u в v, то в нем имеется и простой путь из u в v.

Неориентированный граф называется связным, если любая пара вершин в нем соединена путем. При выполнении такого же условия ориентированный граф называется сильно связным.

Представления графов

Из определения графа следует, что каждый граф G=(V,E) можно задать, непосредственно перечислив его множество вершин V и множество ребер E. Однако такое представление неудобно для решения многих задач о графах. Например, чтобы проверить наличие ребра между двумя вершинам и, придется, вообще говоря, просмотреть все множество E. Хорошее представление, по крайней мере, должно позволить легко переходить от вершины к ее соседу и перечислять всех ее соседей.

В этом параграфе мы рассмотрим три разных способа представления графов, которые более эффективны при решении типичных для теории графов задач.

Матрица (таблица) смежности

Определение 9.5. Матрицей смежности ориентированного (или неориентированного ) графа G=(V,E) с n вершинам и V= { v₁, ... , v_n} называется булева матрица A_G размера n x n с элементами

Это представление позволяет легко проверять наличие ребер между заданными парами вершин. Для поиска всех соседей, в которые ведут ребра из вершины v_i, необходимо просмотреть соответствующую ей i -ю строку матрицы A_G, а чтобы найти вершины, из которых ребра идут в v_i, необходимо просмотреть ее i -ый столбец. Требуемая для A_G память - по порядку n²битов - не может быть уменьшена для графов, у которых "много" ребер. Но для разреженных графов с числом ребер существенно меньшим по порядку n² в матрице смежности много "ненужных" нулей. Для таких графов более эффективными могут оказаться другие представления.

Матрица (таблица) инцидентности

Определение 9.6. Матрицей инцидентности ориентированного (или неориентированного ) графа G=(V,E) с n вершинам и V= { v₁, ... , v_n} и m ребрами E={e₁, ..., e_m} называется матрица B_G размера n x m с элементами

Таким образом, в матрице инцидентности B_G любому ребру e_j = (v_i,v_k) соответствует j -ый столбец, в котором в i -ой строке стоит 1, а в k -ой - -1. Ребра -петли выделяются числом 2. Для проверки наличия ребра между двумя вершинам и v_i и v_k требуется просмотреть i -ю и k -ую строки B_G, поиск всех соседей вершины требует просмотра соответствующей строки. Если m >> n, то это требует существенно больше времени, чем при использовании матрицы смежности. Поэтому при практическом решении задач на графах матрица инцидентности почти не используется.

Списки смежности

Определение 9.7. Пусть G=(V,E) - ориентированный граф, v - вершина из V. Список смежности L_v для вершины v включает все смежные с ней вершины, т.е.

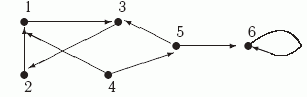
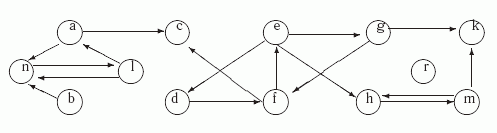
Представление графа G=(V,E) c n вершинам и V= { v₁, ... , v_n} с помощью списков смежности состоит из списков смежности всех вершин: L_v1, L_v2, ... , L_vn.

Размер этого представления сравним с суммой числа вершин и ребер графа. Оно позволяет легко переходить по ребрам от вершины к ее соседям. В программах списки смежностипредставляются списковыми структурами, которые легко реализуются во всех языках программирования.

Пример 9.1. Рассмотрим следующий граф G=(V,E):

Он показан на рис. 9.2.

Построим для него определенные выше представления.

1. Матрица смежности.

2. Матрица инцидентности.

3. Списки смежности.

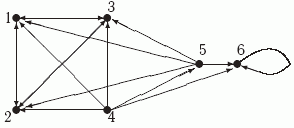
Граф достижимости

Один из первых вопросов, возникающих при изучении графов, это вопрос о существовании путей между заданными или всеми парами вершин. Ответом на этот вопроc - введенное выше отношение достижимости на вершинах графа G=(V,E): вершина w достижима из вершины v, если v = w или в G есть путь из v в w. Иначе говоря, отношение достижимости является рефлексивным и транзитивным замыканием отношения E. Для неориентированных графов это отношение также симметрично и, следовательно, является отношением эквивалентности на множестве вершин V. В неориентированном графе классы эквивалентности по отношению достижимости называются связными компонентами. Для ориентированных графов достижимость, вообще говоря, не должна быть симметричным отношением. Симметричной является взаимная достижимость.

Определение 9.8. Вершины v и w ориентированного графа G=(V,E) называются взаимно достижимыми, если в G есть путь из v в w и путь из w в v.

Ясно, что отношение взаимной достижимости является рефлексивным, симметричным и транзитивным и, следовательно, эквивалентностью на множестве вершин графа. Классы эквивалентности по отношению взаимной достижимости называются компонентами сильной связности или двусвязными компонентами графа.

Рассмотрим вначале вопрос о построении отношения достижимости. Определим для каждого графа его граф достижимости ( называемый иногда также графом транзитивного замыкания),ребра которого соответствуют путям исходного графа.

Определение 9.9. Пусть G=(V,E) - ориентированный граф. Граф достижимости G^*=(V,E^*) для G имеет то же множество вершин V и следующее множество ребер E^* ={ (u, v) | в графеG вершина v достижима из вершины u}.

Пример 9.3. Рассмотрим граф G из примера 9.2.

Рис. 9.2.  Граф G

Тогда можно проверить, что граф достижимости G* для G выглядит так (новые ребра -петли при каждой из вершин 1-5 не показаны):

Рис. 9.3.  Граф G*

Каким образом по графу G можно построить граф G^*? Один способ заключается в том, чтобы для каждой вершины графа G определить множество достижимых из нее вершин, последовательно добавляя в него вершины, достижимые из нее путям и длины 0, 1, 2 и т.д.

Мы рассмотрим другой способ, основанный на использовании матрицы смежности A_G графа G и булевых операций. Пусть множество вершин V={v₁, ... , v_n}. Тогда матрица A_G - это булева матрица размера n x n.

Ниже для сохранения сходства с обычными операциями над матрицами мы будем использовать "арифметические" обозначения для булевых операций: через + будем обозначать дизъюнкцию  а через x - конъюнкцию 

Обозначим через E_n единичную матрицу размера n x n. Положим . Пусть . Наша процедура построения G^* основана на следующем утверждении.

Лемма 9.2. Пусть . Тогда

Доказательство проведем индукцией по k.

Базис. При k=0 и k=1 утверждение справедливо по определению  и .

Индукционный шаг. Пусть лемма справедлива для k. Покажем, что она остается справедливой и для k+1. По определению  имеем:

Предположим, что в графе G из v_i в v_j имеется путь длины <= k+1. Рассмотрим кратчайший из таких путей. Если его длина <= k, то по предположению индукции a_{ij}^{(k)}=1. Кроме того, a_jj⁽¹⁾=1. Поэтому a_ij^(k) a_jj⁽¹⁾=1 и a_ij^(k+1)=1. Если длина кратчайшего пути из из v_i в v_j равна k+1, то пусть v_r - его предпоследняя вершина. Тогда из v_i в v_r имеется путь длиныk и по предположению индукции a_ir^(k)=1. Так как , то a_{rj}^{(1)}=1. Поэтому a_ir^(k) a_rj⁽¹⁾=1 и a_ij^(k+1)=1.

Обратно, если a_ij^(k+1)=1, то хотя бы для одного r слагаемое a_ir^(k) a_rj⁽¹⁾ в сумме равно 1. Если это r=j, то a_ij^(k)=1 и по индуктивному предположению в G имеется путь из v_i в v_jдлины <= k. Если же , то a_ir^(k)=1 и a_rj⁽¹⁾=1. Это означает, что в G имеется путь из v_i в v_r длины <= k и ребро . Объединив их, получаем путь из v_i в v_j длины <= k+1.

Из лемм 9.1 и 9.2 непосредственно получаем

Следствие 1. Пусть G=(V,E) - ориентированный граф с n вершинам и, а G^* - его граф достижимости. Тогда A_{G*} = . Доказательство. Из леммы 5.1 следует, что, если в Gимеется путь из u в , то в нем имеется и простой путь из u в v длины <= n-1. А по лемме 5.2 все такие пути представлены в матрице .

Таким образом процедура построения матрицы смежности A_G* графа достижимости для G сводится к возведению матрицы  в степень n-1. Сделаем несколько замечаний, позволяющих упростить эту процедуру.

1. Для возведения матрицы  в произвольную степень n достаточно выполнить  возведений в квадрат:

где k - это наименьшее число такое, что 2^k >= n.

2. Так как на диагонали в матрице  стоят единицы, то для любых i < j все единицы матрицы  сохраняются в матрице , в частности, и в матрице .

3. Если при вычислении элемента a_ij⁽²⁾ матрицы  по стандартной формуле

обнаруживается такое r, что a_ir = 1 и a_rj =1, то и вся сумма a_ij⁽²⁾ =1. Поэтому остальные слагаемые можно не рассматривать.

Пример 9.3. Рассмотрим в качестве примера вычисление матрицы графа достижимости A_G* для графа G, представленного на рис.9.2. В этом случае

Так как у G имеется 6 вершин, то . Вычислим эту матрицу:

и  (последнее равенство нетрудно проверить). Таким образом,

Как видим, эта матрица действительно задает граф , представленный на рис.9.3.

Взаимная достижимость, компоненты сильной связности и базы графа

По аналогии с графом достижимости определим граф сильной достижимости.

Определение 9.10. Пусть G=(V,E) - ориентированный граф. Граф сильной достижимости G_*^*=(V,E_*^*) для G имеет то же множество вершин V и следующее множество ребер E_*^* ={ (u, v) | в графе G вершины v и u взаимно достижимы}.

По матрице графа достижимости  легко построить матрицу  графа сильной достижимости. Действительно из определений достижимости и сильной достижимостинепосредственно следует, то для всех пар (i,j), 1<= i,j <= n, значение элемента  равно 1 тогда и только тогда, когда оба элемента A_G*(i, j) и A_G*(j, i) равны 1, т.е.

По матрице  можно выделить компоненты сильной связности графа G следующим образом.

1. Поместим в компоненту K₁ вершину v₁ и все такие вершины v_j, что A_{G_*^*}(1,j) = 1.

2. Пусть уже построены компоненты K₁, ..., K_i и v_k - это вершина с минимальным номером, еще не попавшая в компоненты. Тогда поместим в компоненту K_{i+1} вершину v_k и все такие вершины v_j,

3. что A_{G_*^*}(k,j) = 1.

Повторяем шаг (2) до тех пор, пока все вершины не будут распределены по компонентам.

В нашем примере для графа G на рис.2 по матрице  получаем следующую матрицу графа сильной достижимости

Используя описанную выше процедуру, находим, что вершины графа G разбиваются на 4 компоненты сильной связности: K₁= {v₁, v₂, v₃}, \ K₂ ={ v₄}, \ K₃ ={ v₅}, \ K₄ ={ v₆}. На множестве компонент сильной связности также определим отношение достижимости.

Определение 9.11. Пусть K и K' - компоненты сильной связности графа G. Компонента K достижима из компоненты K^\prime, если K= K' или существуют такие две вершины  и , что u достижима из v. K строго достижима из K^\prime, если  и K достижима из K'. Компонента K называется минимальной, если она не является строго достижимой ни из какой компоненты.

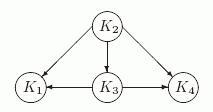
Так как все вершины в одной компоненте взаимно достижимы, то нетрудно понять, что отношения достижимости и строгой достижимости на компонентах не зависят от выбора вершин  и .

Из определения легко выводится следующая характеристика строгой достижимости.

Лемма 9.3. Отношение строгой достижимости является отношением частичного порядка, т.е. оно антирефлексивно, антисимметрично и транзитивно.

Это отношение можно представлять в виде ориентированного графа, вершинам и которого являются компоненты, а ребро (K', K) означает, что K строго достижима из K'. На рис. 9.4показан этот граф компонент для рассматриваемого выше графа G.

Рис. 9.4.  Граф отношения достижимости на компонентах G

В данном случае имеется одна минимальная компонента K₂.

Во многих приложениях ориентированный граф представляет собой сеть распространения некоторого ресурса: продукта, товара, информации и т.п. В таких случаях естественно возникает задача поиска минимального числа таких точек (вершин), из которых этот ресурс может быть доставлен в любую точку сети.

Определение 9.12. Пусть G=(V,E) - ориентированный граф. Подмножество вершин  называется порождающим, если из вершин W можно достичь любую вершину графа. Подмножество вершин  называется базой графа, если оно является порождающим, но никакое его собственное подмножество порождающим не является.

Следующая теорема позволяет эффективно находить все базы графа.

Теорема 9.1. Пусть G=(V,E) - ориентированный граф. Подмножество вершин  является базой G тогда и только тогда, когда содержит по одной вершине из каждой минимальнойкомпоненты сильной связности G и не содержит никаких других вершин.

Доказательство Заметим вначале, что каждая вершина графа достижима из вершины, принадлежащей некоторой минимальной компоненте. Поэтому множество вершин W, содержащих по одной вершине из каждой минимальной компоненты, является порождающим а при удалении из него любой вершины перестает быть таковым, так как вершины из соответствующей минимальной компоненты становятся недостижимы. Поэтому W является базой.

Обратно, если W является базой, то оно обязано включать хотя бы по одной вершине из каждой минимальной компоненты, иначе вершины такой минимальной компоненты окажутся недоступны. Никаких других вершин W содержать не может, так как каждая из них достижима из уже включенных вершин.

Из этой теоремы вытекает следующая процедура построения одной или перечисления всех баз графа G.

1. Найти все компоненты сильной связности G.

2. Определить порядок на них и выделить минимальные относительно этого порядка компоненты.

3. Породить одну или все базы графа, выбирая по одной вершине из каждой минимальной компоненты.

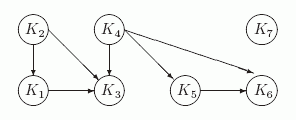
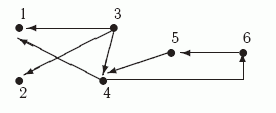
Пример 9.5. Определим все базы ориентированного графа G, показанного на рис.9.5.

Рис. 9.5.  Граф G

На первом этапе находим компоненты сильной связности G:

На втором этапе строим граф строгой достижимости на этих компонентах.

Рис. 9.6.  Граф отношения достижимости на компонентах G

Определяем минимальные компоненты: K₂ = { b }, K₄ ={ d,e, f, g} и K₇= { r}.

Наконец перечисляем все четыре базы G: B₁= { b, d, r}, B₂= { b, e, r}, B₃= { b, f, r} и B₁= { b, g, r}.

Задачи

Задача 9.1. Докажите, что сумма степеней всех вершин произвольного ориентированного графа четна.

У этой задачи имеется популярная интерпретация: доказать, что общее число рукопожатий, которыми обменялись люди, пришедшие на вечеринку, всегда четно.

Задача 9.2. Перечислите все неизоморфные неориентированные графы, у которых не более четырех вершин.

Задача 9.3. Докажите, что неориентированный связный граф остается связным после удаления некоторого ребра  это ребро принадлежит некоторому циклу.

Задача 9.4. Докажите, что неориентированный связный граф с n вершинам и

• содержит не менее n-1 ребер,

• если содержит больше n-1 ребер, то имеет, по крайней мере, хотя бы один цикл.

Задача 9.5. Докажите, что в любой группе из 6 человек есть трое попарно знакомых или трое попарно незнакомых.

Задача 9.6. Докажите, что неориентированный граф G=(V,E) связен  для каждого разбиения  с непустыми V₁ и V₂ существует ребро, соединяющее V₁ с V₂.

Задача 9.7. Докажите, что, если в неориентированном графе имеется ровно две вершины нечетной степени, то они связаны путем.

Задача 9.8. Пусть G=(V,E) неориентированный граф с |E| < |V|-1. Докажите, что тогда G несвязный граф.

Задача 9.9. Докажите, что в связном неориентированном графе любые два простых пути максимальной длины имеют общую вершину.

Задача 9.10. Пусть неориентированный граф без петель G=(V,E) имеет k компонент связности. Доказать, что тогда

Задача 9.11. Определите, что представляет из себя граф достижимости для

• графа с n вершинам и и пустым множеством ребер;

• графа с n вершинам и: V= {v₁,... , v_n}, ребра которого образуют цикл:

Задача 9.12. Вычислите матрицу графа достижимости  для графа

и постройте соответствующий ей граф достижимости. Найдите все базы графа G.

Задача 9.13. Построить для заданного на рис. 9.7 ориентированного графа G₁=(V,E) его матрицу смежности A_G1, матрицу инцидентности B_G1 и списки смежности. Вычислить матрицудостижимости A_G1* и построить соответствующий граф достижимости G₁^*.

Рис. 9.7. 

  ¹⁾   Интересно, что несмотря на внешнюю похожесть задача Эйлера имеет простое эффективное решение (см. задачу 11.1), а задача Гамильтона в общем случае эффективно не решается.