5. Основні властивості нескінченно малих послідовностей

Теорема. Сума (різниця) двох нескінченно малих послідовностей є нескінченно малою послідовністю.

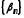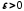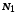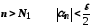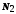Доведення.Нехайі-нескінченно малі послідовності. Задамо довільне. Тоді існує такий номер, що при, й існує такий номер, що при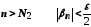. Виберемо. Тоді при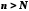виконуватимуться нерівност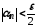іі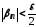. Отже, при

.

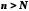
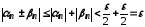Звідси випливає, що послідовності і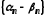нескінченно малі.

Наслідок.Алгебраїчна сума будь-якого скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю.

Теорема. Добуток обмеженої послідовності на нескінченно малу є нескінченно малою послідовністю.

Доведення.Нехай-обмежена послідовність, а-нескінченно мала. Оскільки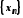обмежена, то існує таке число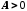, що для всіх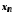виконується нерівність. Задамо довільне. Оскільки послідовність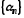нескінченно мала, то існує такий номер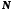, що привиконується нерівність. Отже, при

.

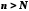
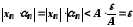Звідси випливає, що послідовність 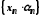нескінченно мала.

Наслідок 1. Добуток нескінченно малої послідовності на число є нескінченно малою послідовністю.

Наслідок 2. Добуток двох нескінченно малих послідовностей є нескінченно малою послідовністю.

Дійсно, якщо послідовність нескінченно мала, то вона обмежена. Отже, добуток двох нескінченно малих послідовностей можна розглядати як добуток нескінченно малої послідовності на обмежену.

Із наслідку 2 випливає, що добуток скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю.

Зауваження. Стосовно частки двох нескінченно малих послідовностей у загальному випадку нічого сказати не можна, оскільки вона може бути нескінченно малою, постійною, нескінченно великою послідовністю або взагалі не визначеною.