
- •Тема 1. Вступ. Дійсні числа лекція 1
- •1. Вступ
- •2. Пончття множини. Дії з множинами
- •Лекція 2
- •1. Загальне поняття відображення або функції
- •2. Потужність множини
- •3. Зчисленні множини
- •4. Математична індукція
- •Лекція 3
- •1. Дійсні числа
- •1. Аксіоми додавання і множення
- •2. Аксіоми порівняння дійсних чисел
- •3. Аксіома неперервності дійсних чисел
- •2. Деякі властивості дійсних чисел
- •Із означення множини дійсних чисел випливає, що ця множина впорядкована.
- •Питання для самостійного опрацювання
- •1. Поняття ізоморфізму
- •2. Інтерпретація множини дійсних чисел
- •3. Найбільш вживані числові множини
- •4. Межі числових множин
- •5. Абсолютна величина числа
- •Абсолютна величина числа позначається символом.
- •Тема 2. Числові послідовності лекція 4
- •1. Означення числової послідовності
- •1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…,
- •2. Арифметичні дії над числовими послідовностями Нехай задано послідовності і.
- •2. Обмежені і необмежені числові послідовності
- •4. Нескінченно малі і нескінченно великі послідовності.
- •5. Основні властивості нескінченно малих послідовностей
2. Деякі властивості дійсних чисел
Наведемо деякі властивості дійсних чисел.
Число
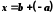 є розв'язком
рівняння
є розв'язком
рівняння
 .
.
Доведення. Підставимо
в дане рівняння замість
 його значення:
його значення:
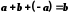 .
.
Згідно з

Згідно з
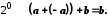
Згідно з
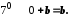
Згідно з

Зауваження.
Число
 називається різницею чисел
називається різницею чисел та
та і позначається
і позначається .
Зазначимо, що за умови
.
Зазначимо, що за умови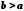 різниця
різниця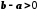 .
Дійсно, якщо
.
Дійсно, якщо ,
то за
,
то за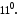 Одержуємо
Одержуємо![]() ,
далі за
,
далі за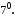 Маємо
Маємо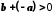 ,
тобто
,
тобто .
.
Число
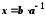 є розв'язком
рівняння
є розв'язком
рівняння
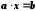 ,
якщо
,
якщо .
.
Доведення.
Підставимо в дане рівняння значення
 :
:
 .
.
Згідно з
 .
.
Згідно з
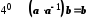 .
.
Згідно з
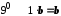 .
.
Згідно з
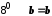 .
.
Зауваження.
Число
 називається часткою чисел
називається часткою чисел й
й і позначається
і позначається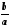 або
або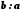 .
.
Якщо
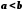 ,
то
,
то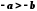 .
.
Дійсно, оскільки
 ,
то
,
то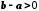 .
Отже, за
.
Отже, за
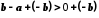 ,
звідки одержуємо
,
звідки одержуємо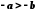 .
.
Зокрема, якщо
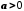 ,
то
,
то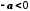 ,
а якщо
,
а якщо ,
то
,
то .
.
Дійсно, згідно з
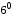
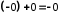 ,
далі за
,
далі за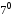
 .
Отже,
.
Отже,
0= − 0.
Якщо
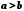 і
і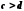 ,
то
,
то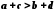 .
.
Дійсно, якщо
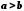 і
і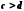 ,
то за
,
то за
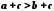 ,
, .
Далі згідно з
.
Далі згідно з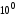
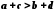 .
.
5. Якщо
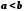 та
та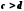 ,
то
,
то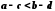 .
.
Дійсно, якщо
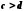 ,
то згідно з
,
то згідно з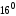
 і за 4
одержуємо:
і за 4
одержуємо:
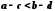 .
.
6.
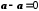 .
.
Це випливає з того,
що
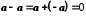 .
.
7.
 .
.
Справді,
 .
.
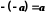 .
.
Дана рівність
доводиться так:
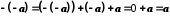 .
.
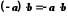 .
.
Доведення:
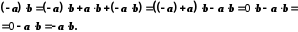
Зокрема,
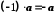 .
.
Якщо
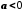 і
і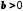 ,
то
,
то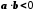 .
.
Дійсно, оскільки
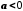 ,
то
,
то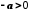 ,
а тому
,
а тому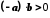 (згідно з
(згідно з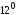 ).
Отже,
).
Отже, ,
а звідси
,
а звідси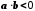 .
.
Якщо
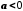 та
та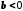 ,
то
,
то .
.
Справді, оскільки
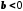 ,
то
,
то ,
а тому
,
а тому (згідно з
(згідно з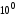 ).
Отже,
).
Отже,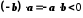 ,
а звідси маємо
,
а звідси маємо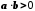 .
.
Якщо
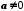 ,
то
,
то .
.
Це випливає з
 і 11.
і 11.
За властивістю
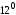 маємо:
маємо: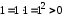 ,
тобто
,
тобто .
.
Надалі будемо використовувати й інші властивості дійсних чисел, не спиняючись на їх формальному доведенні.
Із означення множини дійсних чисел випливає, що ця множина впорядкована.
Множину дійсних
чисел позначатимемо буквою
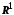 .
.
Питання для самостійного опрацювання
Поняття ізоморфізму.
Інтерпретація множини дійсних чисел.
Найбільш вживані числові множини.
Межі числових множин.
Абсолютна величина числа.
1. Поняття ізоморфізму
Нехай задані дві
множини об'єктів
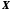 і
і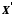 ,
причому в першій визначені деякі
відношення
,
причому в першій визначені деякі
відношення між її об'єктами, а в другій – відношення
між її об'єктами, а в другій – відношення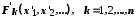 між відповідно своїми об'єктами.
між відповідно своїми об'єктами.
Множини
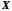 і
і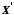 з указаними на них відношеннях називаються
ізоморфними (позначається
з указаними на них відношеннях називаються
ізоморфними (позначається ),
якщо між ними встановлено бієктивне
відображення
),
якщо між ними встановлено бієктивне
відображення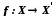 ,
при якому з наявності відношення
,
при якому з наявності відношення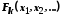 випливає відношення
випливає відношення ,
де
,
де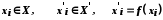 .
.
Будь-яку множину
об'єктів
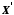 ,
ізоморфну множині
,
ізоморфну множині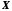 ,
можна розглядати як "модель"
множини
,
можна розглядати як "модель"
множини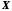 і зводити вивчення властивостей множини
і зводити вивчення властивостей множини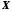 до вивчення властивостей "моделі"
до вивчення властивостей "моделі" .
.
Нехай
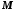 і
і − дві частково впорядковані множини і
нехай
− дві частково впорядковані множини і
нехай .
Якщо з умови
.
Якщо з умови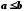 ,
де
,
де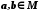 ,
випливає нерівність
,
випливає нерівність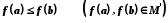 ,
то говорять, що відображення
,
то говорять, що відображення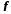 зберігає порядок.
зберігає порядок.
Відображення
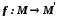 є ізоморфізмом частково впорядкованих
множин
є ізоморфізмом частково впорядкованих
множин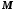 та
та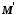 ,
якщо воно бiєктивне,
а співвідношення
,
якщо воно бiєктивне,
а співвідношення
 справджується тоді й тільки тоді, коли
справджується тоді й тільки тоді, коли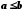 .
Самі множини
.
Самі множини і
і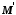 при цьому ізоморфні.
при цьому ізоморфні.
2. Інтерпретація множини дійсних чисел
Розглянемо пряму
з фіксованою точкою
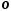 −
початком координат. Нехай задана одиниця
виміру. Тоді множину дійсних чисел
можна поставити у взаємно однозначну
відповідність із точками прямої: точці
−
початком координат. Нехай задана одиниця
виміру. Тоді множину дійсних чисел
можна поставити у взаємно однозначну
відповідність із точками прямої: точці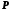 ,
яка лежить справа від точки
,
яка лежить справа від точки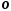 ,
поставимо у відповідність число
,
поставимо у відповідність число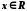 ,
рівне довжині відрізка
,
рівне довжині відрізка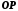 .
Тоді
.
Тоді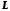 ,
яка лежить зліва від точки
,
яка лежить зліва від точки ,
число
,
число ,
де
,
де – довжина відрізка
– довжина відрізка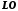 ,
а точці
,
а точці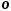 – число 0. Число
– число 0. Число ,
яке відповідає точці
,
яке відповідає точці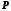 ,
називається координатою точки
,
називається координатою точки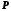 .
Пряма з описаними властивостями
називається числовою прямою. Отже,
кожній точці числової прямої відповідає
дійсне число – її координата. Має місце
й обернене твердження: кожному дійсному
числові
.
Пряма з описаними властивостями
називається числовою прямою. Отже,
кожній точці числової прямої відповідає
дійсне число – її координата. Має місце
й обернене твердження: кожному дійсному
числові відповідає деяка точка числової прямої,
а саме точка
відповідає деяка точка числової прямої,
а саме точка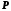 ,
координата якої
,
координата якої .
При так установленій відповідності між
дійсними числами і точками прямої
нерівність
.
При так установленій відповідності між
дійсними числами і точками прямої
нерівність рівносильна тому, що точка з координатою
рівносильна тому, що точка з координатою лежить зліва від точки з координатою
лежить зліва від точки з координатою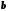 .
Отже, можна говорити про ізоморфізм
множини дійсних чисел і множини точок
числової прямої, тобто що числова пряма
є моделлю множини дійсних чисел.
.
Отже, можна говорити про ізоморфізм
множини дійсних чисел і множини точок
числової прямої, тобто що числова пряма
є моделлю множини дійсних чисел.
Надалі, говорячи про дійсні числа, замість слова "число" іноді вживається слово "точка". У зв'язку з цим числові множини ще називають точковими.
Використовуючи
аксіому неперервності множини дійсних
чисел, можна встановити, що множина
дійсних чисел, яка задовольняє умову
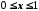 ,
є незчисленною. Говорять, що ця множина
має потужність континууму. Із цього
випливає, що множина всіх дійсних чисел
незчисленна. Можна також довести, що
множина раціональних чисел зчисленна.
Отже, множина ірраціональних чисел
незчисленна, оскільки вона є множиною
,
є незчисленною. Говорять, що ця множина
має потужність континууму. Із цього
випливає, що множина всіх дійсних чисел
незчисленна. Можна також довести, що
множина раціональних чисел зчисленна.
Отже, множина ірраціональних чисел
незчисленна, оскільки вона є множиною (якби множина
(якби множина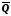 ірраціональних чисел була зчисленною,
то і множина
ірраціональних чисел була зчисленною,
то і множина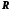 була б зчисленною, оскільки
була б зчисленною, оскільки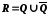 ).
).
