
- •Тема 1. Вступ. Дійсні числа лекція 1
- •1. Вступ
- •2. Пончття множини. Дії з множинами
- •Лекція 2
- •1. Загальне поняття відображення або функції
- •2. Потужність множини
- •3. Зчисленні множини
- •4. Математична індукція
- •Лекція 3
- •1. Дійсні числа
- •1. Аксіоми додавання і множення
- •2. Аксіоми порівняння дійсних чисел
- •3. Аксіома неперервності дійсних чисел
- •2. Деякі властивості дійсних чисел
- •Із означення множини дійсних чисел випливає, що ця множина впорядкована.
- •Питання для самостійного опрацювання
- •1. Поняття ізоморфізму
- •2. Інтерпретація множини дійсних чисел
- •3. Найбільш вживані числові множини
- •4. Межі числових множин
- •5. Абсолютна величина числа
- •Абсолютна величина числа позначається символом.
- •Тема 2. Числові послідовності лекція 4
- •1. Означення числової послідовності
- •1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…,
- •2. Арифметичні дії над числовими послідовностями Нехай задано послідовності і.
- •2. Обмежені і необмежені числові послідовності
- •4. Нескінченно малі і нескінченно великі послідовності.
- •5. Основні властивості нескінченно малих послідовностей
Тема 2. Числові послідовності лекція 4
Означення числової послідовності.
Арифметичні дії з числовими послідовностями.
Обмежені і необмежені числові послідовності.
Нескінченно малі і нескінченно великі послідовності.
Основні властивості нескінченно малих послідовностей.
1. Означення числової послідовності
Числовою послідовністю
називається відображення
 .
.
Отже, якщо кожному
натуральному числові
 поставлено у відповідність дійсне число
поставлено у відповідність дійсне число ,
то множина дійсних чисел
,
то множина дійсних чисел
 (1)
(1)
називається числовою послідовністю.
Числа
 називаються елементами (або членами)
послідовності. Символ
називаються елементами (або членами)
послідовності. Символ називається загальним елементом
послідовності, а
називається загальним елементом
послідовності, а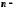 його номером. Скорочено послідовність
(1) позначається так:
його номером. Скорочено послідовність
(1) позначається так: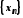 .
Наприклад,
.
Наприклад, є
послідовність
є
послідовність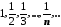 .
.
Послідовність
вважається заданою, якщо вказано правило,
за яким кожному натуральному числові
 поставлено у відповідність дійсне
число
поставлено у відповідність дійсне
число .
Найчастіше числову послідовність
задають формулою загального (
.
Найчастіше числову послідовність
задають формулою загального (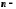 го)
члена послідовності:
го)
члена послідовності: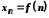 .
Наприклад, формула
.
Наприклад, формула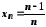 задає числову послідовність
задає числову послідовність
![]()
Числову послідовність
можна задати рекурентною формулою,
тобто формулою, в якій указується
правило, за котрим можна виразити
наступний її член через попередні.
Наприклад, арифметична прогресія з
першим членом
 та різницею
та різницею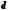 визначається рекурентною формулою
визначається рекурентною формулою
 або
або
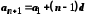 .
.
Рекурентною формулою
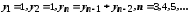
задається послідовність
1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…,
що відома в математиці як " ряд Фібоначчі", а її члени – як числа Фібоначчі. Ці числа мають ряд цікавих властивостей. Нині вони використовуються при обробці інформації на ЕОМ, при відшуканні оптимальних методів програмування тощо.
2. Арифметичні дії над числовими послідовностями Нехай задано послідовності і.
Добутком
послідовності
 на число
на число називається послідовність
називається послідовність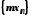 ,
тобто
,
тобто
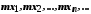 .
.
Сумою послідовностей
 і
і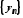 називається послідовність
називається послідовність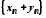 :
:
 ;
;
різницею –
послідовність
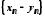 :
:
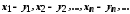 ;
;
добутком –
послідовність
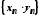 :
:
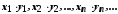 ;
;
часткою -
послідовність
 :
:
 ;
де
;
де
 .
.
2. Обмежені і необмежені числові послідовності
Послідовність
 називається обмеженою зверху, якщо
існує таке число
називається обмеженою зверху, якщо
існує таке число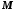 ,
що для всіх її членів
,
що для всіх її членів виконується нерівність
виконується нерівність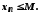
Послідовність
 називається обмеженою знизу, якщо існує
таке число
називається обмеженою знизу, якщо існує
таке число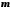 ,
що для всіх її членів
,
що для всіх її членів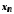 виконується нерівність
виконується нерівність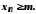
Послідовність
 називається обмеженою, якщо вона обмежена
зверху й знизу.
називається обмеженою, якщо вона обмежена
зверху й знизу.
Нехай
послідовність
 обмежена, тобто існують такі числа
обмежена, тобто існують такі числа і
і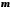 ,
що для будь-якого її члена
,
що для будь-якого її члена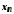 виконується нерівність
виконується нерівність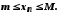 Нехай
Нехай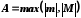 .
Тоді умову обмеженості послідовності
можна записати так:
.
Тоді умову обмеженості послідовності
можна записати так: .
.
Послідовність
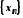 називається необмеженою, якщо для
будь-якого числа
називається необмеженою, якщо для
будь-якого числа існує елемент
існує елемент цієї послідовності, для якого виконується
нерівність
цієї послідовності, для якого виконується
нерівність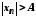 .
.
Зауваження. Необмежена послідовність може бути обмеженою зверху або знизу.
Приклади.
Послідовність
 обмежена знизу (
обмежена знизу ( ),
але не обмежена зверху.
),
але не обмежена зверху.
Послідовність
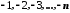 обмежена зверху (
обмежена зверху (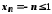 ),
але не обмежена знизу.
),
але не обмежена знизу.
Послідовність
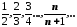 обмежена зверху і знизу (
обмежена зверху і знизу ( ).
).
Послідовність
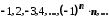 не обмежена.
не обмежена.
4. Нескінченно малі і нескінченно великі послідовності.
Послідовність
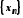 називається
нескінченно великою, якщо для будь-якого
числа
називається
нескінченно великою, якщо для будь-якого
числа
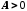 існує такий номер
існує такий номер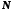 ,
що для всіх елементів
,
що для всіх елементів із номером
із номером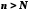 виконується нерівність
виконується нерівність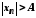 .
.
Зауваження.У наведеному означенні
номер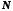 залежить від числа
залежить від числа ,
тобто
,
тобто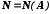 .
.
Очевидно, що всяка нескінченно велика
послідовність є необмеженою, проте не
всяка необмежена послідовність є
нескінченно великою. Наприклад, необмежена
послідовність 0, 1, 0, 2,
0, 3, ..., n,
0, n+1,
… не є нескінченно
великою, оскільки не існує такого номера ,
щоб для всіх
,
щоб для всіх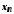 ,
де
,
де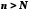 виконувалася б, наприклад, нерівність
виконувалася б, наприклад, нерівність .
.
Послідовність
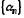 називається нескінченно малою, якщо
для будь-якого (як завгодно малого) числа
називається нескінченно малою, якщо
для будь-якого (як завгодно малого) числа
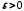 існує
такий номер
існує
такий номер
 ,
що для всіх елементів
,
що для всіх елементів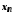 із номером
із номером
 виконується
нерівність
виконується
нерівність
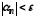 .
.
Зауваження.У наведеному означенні
номер залежить від числа
залежить від числа ,
тобто
,
тобто
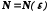 .
.
Приклад 1.Показати, що послідовність
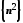 є нескінченно великою.
є нескінченно великою.
Нехай маємо довільне число
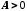 .
Із нерівності
.
Із нерівності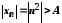 або
або .
.
Покладемо
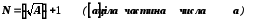 .
.
Тоді
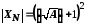 .
Оскільки
.
Оскільки ,
то
,
то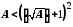 .
Отже, при
.
Отже, при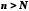 виконується нерівність
виконується нерівність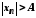 .
.
Приклад 2.Показати, що послідовність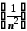 є нескінченно малою.
є нескінченно малою.
Нехай маємо довільне число
 .
Із нерівності
.
Із нерівності одержуємо
одержуємо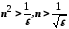 .
Покладемо
.
Покладемо .
Тоді для всіх
.
Тоді для всіх маємо
маємо ,
тобто
,
тобто або
або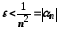 .
.
Теорема.Якщо -нескінченно велика
послідовність і всі її члени відмінні
від нуля, то послідовність
-нескінченно велика
послідовність і всі її члени відмінні
від нуля, то послідовність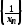 нескінченно мала, і, навпаки, якщо
нескінченно мала, і, навпаки, якщо -нескінченно мала
послідовність й
-нескінченно мала
послідовність й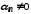 ,
то послідовність
,
то послідовність нескінченно велика.
нескінченно велика.
Доведення.
Нехай
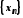 -
нескінченно велика послідовність.
Візьмемо довільне
-
нескінченно велика послідовність.
Візьмемо довільне
 і покладемо
і покладемо .
Оскільки
.
Оскільки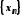 нескінченно велика послідовність, то
для вказаного
нескінченно велика послідовність, то
для вказаного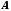 існує номер
існує номер такий, що при
такий, що при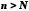 виконується нерівність
виконується нерівність .
Звідси маємо
.
Звідси маємо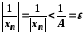 .
Отже, послідовність
.
Отже, послідовність -
нескінченно мала.
-
нескінченно мала.
Друга частина теореми доводиться аналогічно.
