
- •Тема 1. Вступ. Дійсні числа лекція 1
- •1. Вступ
- •2. Пончття множини. Дії з множинами
- •Лекція 2
- •1. Загальне поняття відображення або функції
- •2. Потужність множини
- •3. Зчисленні множини
- •4. Математична індукція
- •Лекція 3
- •1. Дійсні числа
- •1. Аксіоми додавання і множення
- •2. Аксіоми порівняння дійсних чисел
- •3. Аксіома неперервності дійсних чисел
- •2. Деякі властивості дійсних чисел
- •Із означення множини дійсних чисел випливає, що ця множина впорядкована.
- •Питання для самостійного опрацювання
- •1. Поняття ізоморфізму
- •2. Інтерпретація множини дійсних чисел
- •3. Найбільш вживані числові множини
- •4. Межі числових множин
- •5. Абсолютна величина числа
- •Абсолютна величина числа позначається символом.
- •Тема 2. Числові послідовності лекція 4
- •1. Означення числової послідовності
- •1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…,
- •2. Арифметичні дії над числовими послідовностями Нехай задано послідовності і.
- •2. Обмежені і необмежені числові послідовності
- •4. Нескінченно малі і нескінченно великі послідовності.
- •5. Основні властивості нескінченно малих послідовностей
3. Найбільш вживані числові множини
Нехай
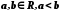 .
Будемо використовувати наступні
позначення:
.
Будемо використовувати наступні
позначення:
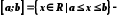 відрізок,
відрізок,
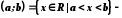 інтервал,
інтервал,
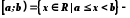 півінтервал,
півінтервал,
 півінтервал.
півінтервал.
Указані множини
ще називають проміжками. Ми розглядатимемо
також і нескінченні множини, використовуючи
для цього символи
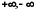 .
.

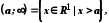
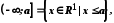


Околом точки
 називається довільний інтервал
називається довільний інтервал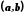 ,
який містить точку
,
який містить точку
 ,
тобто
,
тобто
 .
.
Інтервал
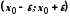 називається
називається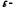 околом
точки
околом
точки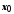 .
Точка
.
Точка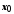 називається центром цього околу, а число
називається центром цього околу, а число
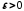 його
радіусом. Зазвичай так позначають околи
з центром у точці
його
радіусом. Зазвичай так позначають околи
з центром у точці
 і дуже
малим радіусом, тобто коли
і дуже
малим радіусом, тобто коли
 досить мале.
досить мале.
4. Межі числових множин
Нехай задано
непорожню числову множину
 .
.
Множина
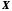 називається обмеженою зверху, якщо
існує таке дійсне число
називається обмеженою зверху, якщо
існує таке дійсне число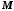 ,
що для кожного
,
що для кожного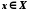 виконується нерівність
виконується нерівність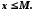
Множина
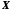 називається обмеженою знизу, якщо існує
таке дійсне число
називається обмеженою знизу, якщо існує
таке дійсне число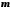 ,
що для кожного
,
що для кожного виконується нерівність
виконується нерівність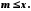
При цьому числа
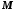 і
і називаються відповідно верхньою та
нижньою межею множини
називаються відповідно верхньою та
нижньою межею множини .
.
Множина, яка обмежена зверху й знизу, називається обмеженою.
Очевидно, що
будь-яка обмежена зверху (знизу) множина
 має безліч верхніх (нижніх) меж.
має безліч верхніх (нижніх) меж.
Найменша верхня
межа обмеженої зверху множини
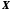 називається точною верхньою межею або
верхньою гранню цієї множини і
позначається
називається точною верхньою межею або
верхньою гранню цієї множини і
позначається (supremum
(лат.) – найвище).
(supremum
(лат.) – найвище).
Найбільша нижня
межа обмеженої знизу множини
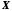 називається точною нижньою межею або
нижньою гранню цієї множини і позначається
називається точною нижньою межею або
нижньою гранню цієї множини і позначається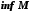 (infimum
(лат.) – найнижче).
(infimum
(лат.) – найнижче).
Якщо
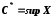 ,
то для довільного числа
,
то для довільного числа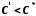 існує
існує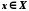 таке, що
таке, що .
Якщо
.
Якщо , то для довільного числа
, то для довільного числа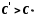 існує
існує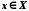 таке, що
таке, що .
.
Теорема. Будь-яка непорожня обмежена зверху числова множина має точну верхню межу. Якщо ж вона обмежена знизу, то має точну нижню межу.
Доведення.
Нехай
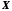 – непорожня обмежена зверху числова
множина. Тоді множина
– непорожня обмежена зверху числова
множина. Тоді множина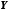 чисел, які обмежують
чисел, які обмежують зверху, непорожня. Із означення верхньої
межі випливає, що
зверху, непорожня. Із означення верхньої
межі випливає, що виконується нерівність
виконується нерівність .
За аксіомою неперервності дійсних чисел
існує таке число
.
За аксіомою неперервності дійсних чисел
існує таке число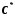 ,
що
,
що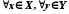 виконується нерівність
виконується нерівність .
.
Із цієї нерівності
випливає, що
 обмежує
обмежує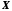 зверху, тобто є верхньою межею, і є
найменшим із усіх верхніх меж, тобто є
точною верхньою межею.
зверху, тобто є верхньою межею, і є
найменшим із усіх верхніх меж, тобто є
точною верхньою межею.
Друга частина теореми доводиться аналогічно.
Якщо множина
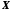 не обмежена зверху ( знизу ), то за
домовленістю пишуть
не обмежена зверху ( знизу ), то за
домовленістю пишуть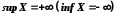 .
.
5. Абсолютна величина числа
Абсолютною
величиною
(модулем) числа
 називається саме число
називається саме число ,
якщо
,
якщо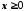 ,
число –
,
число – ,
якщо
,
якщо .
.
Абсолютна величина числа позначається символом.

Із означення
абсолютної величини випливає, що
нерівності
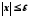 і
і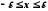 ,
де
,
де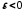 рівносильні, тобто
рівносильні, тобто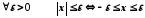 .
.
Теорема.
Абсолютна величина суми двох чисел не
більше від суми абсолютних величин
чисел, тобто
 .
.
Доведення. За означення абсолютної величини

для будь-яких чисел
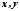 .
Додаючи почленно ці нерівності, одержимо
.
Додаючи почленно ці нерівності, одержимо
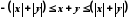 .
.
Остання нерівність рівносильна нерівності
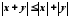 .
.
Теорема. Абсолютна величина різниці двох чисел не менше від різниці абсолютних величин чисел, тобто
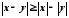 .
.
Доведення.
Для будь-яких чисел
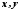 маємо
маємо

За попередньою теоремою
 .
.
Звідси одержуємо
 .
.
Зазначимо, що
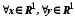 мають місце співвідношення
мають місце співвідношення

