Лекція 2

1. Загальне поняття відображення або функції.

2. Потужність множини.

3. Зчисленні множини.

4. Математична індукція.

1. Загальне поняття відображення або функції

Нехай X і Y дві множини. Відображенням f множини X у множину Y називається правило, яке кожному елементу ставить у відповідність один і тільки один елемент .

Замість слова "відображення" можна вживати "функція", "оператор", "відповідність".

Записи 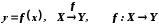означають, щоf є відображенням множини X у множину Y.

Для позначення функції вживаються й інші букви, наприклад .

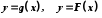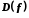Елемент y, який відображення f ставить у відповідність елементу , називається образом елементапри відображенніf або значенням відображення f у точці і позначається символом . Множина X називається областю визначення відображення f і позначається . Множина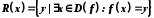називається множиною значень відображення f.

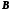Нехай . Образом множиниA при відображенні f називається множина . Прообразом множинипри відображенніназивається множина.

Графіком функції 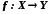називається множина.

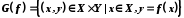Якщо 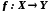і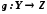, то функція, яка визначається формуламиназивається складеною функцією, або суперпозицією функційf і g.

Приклади.

Відображення 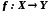називається відображенням множиниХ на множину 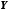або сур'єкцією, якщо .

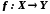Відображення називається взаємооднозначним відображенням множини X у множину Y або ін'єкцією, якщо

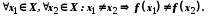
Відображення 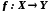, яке є сур'єкцією та ін'єкцією, називається бієкцією. У цьому випадку говорять, щоздійснює взаємно однозначну відповідність між множинамиі.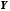

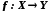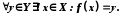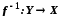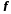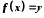Якщо − бієкція, тоФункціяназивається оберненою до бієкції, якщота.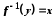

Відображення 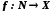називається послідовністю елементів із. Послідовність позначається так:де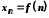− -ний член послідовності.

2. Потужність множини

Множина, яка складається із скінченного числа елементів, називається скінченною. Для скінченної множини 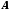число її елементів позначається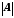. Скінченні множини можна порівнювати за кількістю їх елементів. Виникає питання, як можна порівнювати нескінченні множини? Г. Кантор побудував теорію, яка містить відповідь на поставлене питання. Вихідним пунктом цієї теорії є поняття потужності множини.

Множини 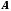і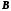називаються рівнопотужними (мають однакову потужність), якщо існує бієкція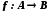. Рівнопотужні множини позначають так: A ~ B.

3. Зчисленні множини

Множина називається зчисленною, якщоA ~ N. У цьому випадку говорять, що елементи множини можна занумерувати.

Мають місце наступні твердження:

1. Нескінченна підмножина зчисленної множини зчисленна.

2. Нескінченна множина містить зчисленну підмножину.

3. Об'єднання зчисленної множини зчисленних множин є зчисленною множиною.

4. Декартів добуток двох зчисленних множин зчисленний.

5. Існують незчисленні множини.

Доведення першого і другого твердження досить прості. Їх пропонується виконати самостійно. Спинимось на доведенні твердження 3.

Нехай - зчисленні множини. Тоді для кожного.

Елементи об'єднання цих множин можна подати у вигляді таблиці

……

……

……

…………………………………………

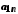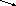
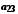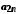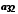
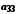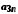і занумерувати, наприклад у порядку, вказаному стрілками. Цим саме буде встановлена бієкція 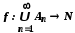. Отже,.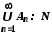

Аналогічно доводиться твердження 4.

Нехай . Тоді декартів добуток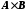складається із пар, які можна розташувати в такому порядку

і занумерувати так, як зроблено в попередньому випадку.

Для доведення твердження 5 застосуємо діагональний метод (діагональну процедуру) Кантора.

Нехай − множина всіх можливих нескінченних ланцюгів, що складаються з двох символів, наприклад 0 і 1, вигляду

Покажемо, що множина 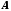незчисленна. Припустимо, що елементи множинизанумеровані, тобто що множиназчисленна. Нехай

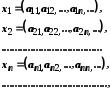
де кожне дорівнює 0 або 1. Утворимо елемент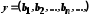, поклавши 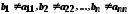, і кожне відповідно дорівнює 0 або 1. Очевидно, що , але не збігається з жодним із занумерованих елементів. А це суперечить тому, що всі елементи множини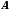можна занумерувати.