5.6. Выбор налогов

Даже тот маленький кусочек теории потребительского выбора, который удалось рассмотреть выше, можно использовать для выведения интересных и важных умозаключений. Вот неплохой пример, в котором описывается выбор одного из двух типов налогов. Как мы видели, налог на объем покупок есть налог на потребляемое количество товара, подобный налогу на бензин, составляющему 15 центов за галлон. Подоходный налог — это просто налог на доход. Допустим, правительство хочет собрать некоторую сумму дохода. Каким способом предпочтительнее это сделать — посредством налога на объем покупок или же посредством подоходного налога? Для ответа на этот вопрос воспользуемся уже полученными нами знаниями.

Во-первых, проанализируем введение налога на объем покупок. Предположим, что исходное бюджетное ограничение имеет вид

p₁x₁ + p₂x₂ = m.

Каким станет бюджетное ограничение, если ввести налог на потребление товара 1 по ставке t ? Ответ прост. С точки зрения потребителя, это все равно, что поднять цену товара 1 на величину t. Следовательно, новое бюджетное ограничение будет иметь вид

. (5.1)

Таким образом, налог на объем покупок повышает цену для потребителя. На рис.5.9 показан пример возможного влияния изменений цены на спрос. На этой стадии мы не знаем с уверенностью, увеличит или уменьшит данный налог потребление товара 1, хотя есть основания предполагать, что он его уменьшит. Как бы то ни было, мы знаем наверняка, что оптимальный выбор (,3) должен удовлетворять бюджетному ограничению

. (5.2)

Доход, собранный благодаря введению этого налога, составляет 4.

Теперь рассмотрим подоходный налог, приносящий такую же сумму дохода. Бюджетное ограничение в этом случае примет вид

p₁x₁ + p₂x₂ = m — R*,5

или, если мы подставим в него выражение для R*,

p₁x₁ + p₂x₂ = m — t.6

Каким образом пройдет эта бюджетная линия на рис. 5.9?

Нетрудно заметить, что она имеет тот же наклон, —p₁/p₂7, что и исходная бюджетная линия, однако местоположение новой бюджетной линии предстоит определить. Оказывается, бюджетная линия для случая введения подоходного налога должна пройти через точку (,8). Чтобы проверить это, подставим (,9) в бюджетное ограничение для случая подоходного налога и посмотрим, не нарушается ли равенство.

Верно ли, что

p₁+p₂ = m — t?10

Да, поскольку это не что иное, как результат преобразования уравнения (5.2), которое, как мы знаем, справедливо.

Тем самым установлено, что (,11) лежит на бюджетной линии для случая подоходного налога: это допустимый выбор для потребителя. Но является ли он оптимальным? Легко увидеть, что не является. В точке (,12) MRS равна —(p₁ + t)/p₂13. Но введение подоходного налога позволяет нам обменивать товары в пропорции —p₁/p₂14. Следовательно, бюджетная линия пересекает кривую безразличия в точке (,15), а это подразумевает существование на бюджетной линии некой точки, предпочитаемой (,16).

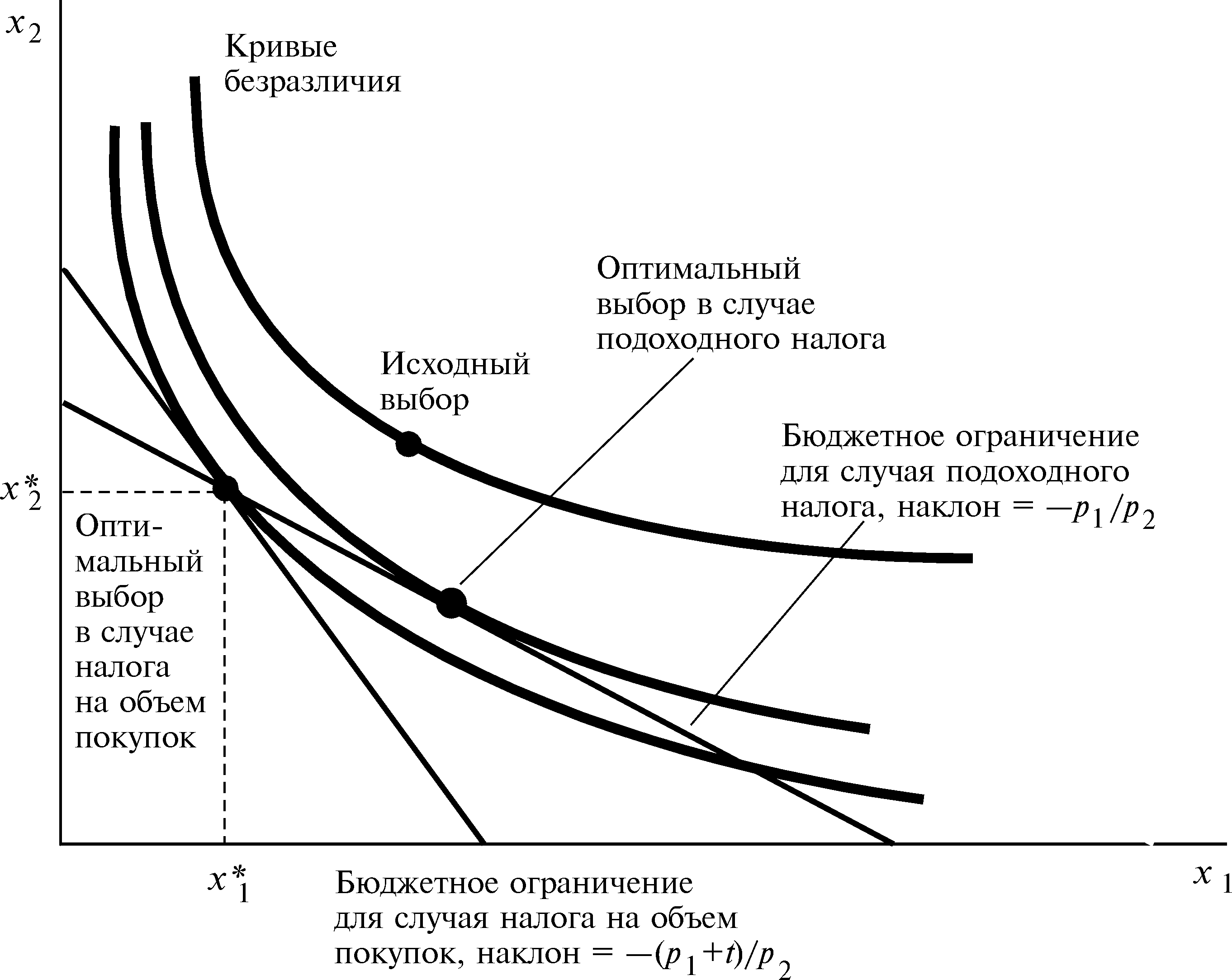
Сопоставление подоходного налога и налога на объем покупок. Рассмотрим налог на объем покупок, приносящий доход R*17, и подоходный налог, приносящий такой же доход. Благосостояние потребителя окажется более высоким при подоходном налоге, так как в этом случае он может выбрать точку на более высокой кривой безразличия.

Рис. 5.9

Таким образом, подоходный налог явно предпочтительнее налога на объем покупок в том смысле, что позволяет собрать с потребителя ту же сумму дохода, сохраняя при этом более высокий уровень его благосостояния.

Это неплохой результат, и его стоит запомнить, но важно также понять его ограниченность. Во-первых, он относится только к одному потребителю. Проведенные рассуждения показывают, что для каждого данного потребителя существует подоходный налог, позволяющий получить от этого потребителя такую же сумму денег, что и с помощью налога на объем покупок, и сохранить при этом более высокий уровень его благосостояния. Однако размеры этого подоходного налога обычно различаются от потребителя к потребителю. Поэтому единый подоходный налог для всех потребителей не обязательно лучше, чем единый налог на объем покупок для всех потребителей. (Представим себе случай, когда какой-то потребитель совсем не потребляет товара 1 — этот индивид, безусловно, предпочтет единому подоходному налогу налог на объем покупок.)

Во-вторых, мы предположили, что при введении подоходного налога доход потребителя не меняется. Тем самым мы предположили, что подоходный налог есть аккордный налог, т.е. такой налог, который изменяет лишь сумму денег, расходуемую потребителем, не влияя при этом на потребительский выбор. Однако такая предпосылка нереалистична. Если потребитель зарабатывает свой доход, можно ожидать, что введение налога на доход уменьшит стимулы к заработкам, так что доход после налогообложения может уменьшиться даже на большую сумму, чем та, которая изымается посредством налога.

В-третьих, мы совершенно упустили из виду реакцию на налог со стороны предложения. Мы показали, какова реакция спроса на изменения налогообложения, но реакция предложения также будет иметь место, и для полноты анализа эти изменения тоже следует учесть.

Краткие выводы

1. Оптимальный выбор потребителя есть тот принадлежащий бюджетному множеству данного потребителя набор, который находится на самой высокой кривой безразличия.

2. Как правило, оптимальный набор характеризуется соблюдением условия равенства наклона кривой безразличия (MRS) наклону бюджетной линии.

3. При наблюдении нескольких случаев потребительского выбора возможно построение оценочной функции полезности, которая могла бы обусловить потребительское поведение данного рода. Такую функцию полезности можно использовать для прогнозирования будущего потребительского выбора и в целях оценки полезности новой экономической политики для потребителей.

4. Если цены двух товаров одинаковы для всех потребителей, то предельная норма замещения будет у всех потребителей одна и та же, и, следова-тельно, каждый из них будет готов обменять указанные товары в одной и той же пропорции.

ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ

1. Какова функция спроса на товар 2 в случае, если два товара являются совершенными субститутами?

2. Предположим, что кривые безразличия представляют собой прямые линии с наклоном, равным —b. Как будет выглядеть оптимальный выбор потребителя при заданных произвольных ценах p₁, p₂ и денежном доходе m?

3. Предположим, что потребитель всегда выпивает одну чашку кофе с двумя ложками сахара. Сколько кофе и сахара захочет купить потребитель, если цена ложки сахара равна p₁18, цена чашки кофе равна p₂19 и потребитель может потратить на эти товары m долларов?

4. Предположим, что ваши предпочтения в отношении мороженого и оливок описываются вогнутыми кривыми безразличия, подобными приведенным в тексте настоящей главы, и что вы можете потратить на эти товары m долларов, а их цены составляют соответственно p₁20 и p₂21. Перечислите варианты выбора оптимальных потребительских наборов.

5. Если функция полезности для данного потребителя имеет вид u(x₁, x₂) = = x₁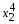22, то какую долю своего дохода он будет тратить на товар 2?

6. При какого рода предпочтениях благосостояние потребителя будет одинаковым как в случае налога на объем покупок, так и в случае подоходного налога?

ПРИЛОЖЕНИЕ

Весьма полезно уметь решать задачу максимизации полезности при заданных предпочтениях, получая при этом алгебраические примеры реально встречающихся функций полезности. В тексте главы мы проделали это для таких простых случаев, как совершенные субституты и совершенные комплементы, а в настоящем приложении посмотрим, как это делается в более общих случаях.

Во-первых, обычно мы будем стремиться к тому, чтобы представить предпочтения потребителя функцией полезности u(x₁, x₂)23. Как мы видели в гл. 4, данная предпосылка не накладывает слишком серьезных ограничений, поскольку большую часть стандартных предпочтений можно описать с помощью функции полезности.

Прежде всего заметим, что нам уже известно, как решать задачу на нахождение оптимального выбора потребителя. Требуется лишь свести воедино все изученное нами в трех последних главах. Из настоящей главы мы знаем, что оптимальный выбор (x₁, x₂24) должен удовлетворять условию

MRS (x₁, x₂) = —, (5.3)

а в приложении к гл. 4 мы видели, что MRS можно выразить в виде отношения производных функции полезности, взятого с обратным знаком. Произведя эту подстановку и сократив знаки "минус", получаем

. (5.4)

Из гл. 2 известно, что оптимальный выбор должен удовлетворять также бюджетному ограничению

p₁x₁ + p₂x₂ = m. (5.5)

Получаем два уравнения — для условия, связанного с MRS, и для бюджетного ограничения — с двумя неизвестными x₁25 и x₂26. Остается лишь решить эти уравнения, найдя оптимальный выбор x₁27 и x₂28 как функцию цен и дохода. Имеется ряд способов решения двух уравнений с двумя неизвестными. Один из них, который всегда применим, хотя, возможно, и не всегда оказывается самым простым, состоит в том, чтобы выразить из бюджетного ограничения одно неизвестное и подставить полученное выражение в условие для MRS.

Переписав бюджетное ограничение, получаем

x₂29 =—x₁,30 (5.6)

а подставив это выражение для x₂31 в уравнение (5.4), получаем

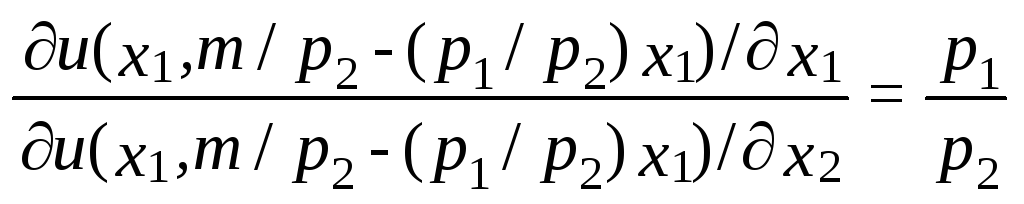32.

Это достаточно громоздкое с виду выражение содержит лишь одну неизвестную переменную x₁33, и ее значение обычно можно выразить через (p₁, p₂, m). Затем из бюджетного ограничения можно получить решение для x₂34 как функции цен и дохода.

Можно вывести и более строгое решение задачи максимизации полезности, используя условия существования максимума функции, известные из курса дифференциального исчисления. Для этого сначала представим задачу максимизации полезности в виде задачи на нахождение условного максимума:

max u(x₁, x₂) 35

x₁, x₂ 36

при p₁x₁ + p₂x₂ = m 37.

Эта задача требует выбора таких значений x₁38 и x₂39, которые, во-первых, удовлетворяли бы данному ограничению, а во-вторых, давали бы большую величину полезности u(x₁, x₂)40, чем любые другие значения x₁41 и x₂42, которые ему удовлетворяют.

Существуют два способа решения задачи такого рода. Первый заключается в том, чтобы из бюджетного ограничения просто выразить одну переменную через другую, а затем подставить полученное выражение в целевую функцию.

Например, для любого заданного значения x₁43 количество x₂44, требуемое для того, чтобы удовлетворялось бюджетное ограничение, задано линейной функцией

x₂(x₁)4546 = —x₁ (5.7)

Теперь подставим в функцию полезности x₂(x₁)4748 вместо x₂ и получим задачу на нахождение безусловного максимума

max u(x₁, m/p₂ — (p₁/p₂)x₁)49.

x₁50

Это задача на нахождение безусловного максимума только по x₁51, поскольку мы использовали функцию x₂ (x₁)52 для того, чтобы гарантировать, что значение x₂53 всегда будет удовлетворять бюджетному ограничению, каково бы ни было значение x₁54.

Задача решается, как обычно, путем взятия производной функции полезности по x₁55 и приравнивания ее к нулю. В результате получим условие первого порядка в виде

. (5.8)

Первый член этого выражения отражает прямое воздействие возрастания x₁56 на возрастание полезности. Второй член состоит из двух частей: du/dx₂5758 — скорости возрастания полезности по мере роста x₂59, умноженной на dx₂/dx₁60 — скорость возрастания x₂61 по мере роста x₁62 в связи с необходимостью удовлетворения уравнению бюджетной линии. Чтобы подсчитать эту последнюю производную, продифференцируем выражение (5.7)

= —63.

Подстановка полученного результата в (5.8) даст выражение

64,

говорящее лишь о том, что предельная норма замещения товаров x₁65 и x₂66 в точке оптимального выбора (,67) должна быть равна отношению цен. Это именно то условие, которое мы вывели ранее: наклон кривой безразличия должен равняться наклону бюджетной линии. Разумеется, оптимальный выбор должен удовлетворять и бюджетному ограничению p₁68+p₂69=m70, что снова дает нам два уравнения с двумя неизвестными.

Второй способ решения таких задач заключается в использовании множителей Лагранжа. Применение этого метода начинается с составления вспомогательной функции, известной как функция Лагранжа:

L = u(x₁, x₂) — (p₁x₁ + p₂x₂ — m) 71

Новая переменная 72 именуется множителем Лагранжа, так как на нее умножается ограничение. Согласно теореме Лагранжа, оптимальный выбор (,73) должен удовлетворять трем условиям первого порядка

—lp₁ = 0,74

—lp₂ = 0,75

—m = 076.

Три этих уравнения характеризуются несколькими интересными моментами. Во-первых, они представляют собой просто приравненные к нулю производные функции Лагранжа по x₁, x₂ и 77. Последняя производная, по 78, есть не что иное, как бюджетное ограничение. Во-вторых, теперь у нас имеются три уравнения с тремя неизвестными x₁, x₂ и 79. Мы надеемся получить их решения для x₁ и x₂80, выраженные через p₁, p₂ и m.

Доказательство теоремы Лагранжа можно найти в любом учебнике по дифференциальному исчислению продвинутого уровня. Эта теорема очень широко используется в продвинутых курсах экономической теории, для наших же целей требуется знать лишь формулировку данной теоремы и как ее применять.

В нашем конкретном случае стоит обратить внимание на то, что, поделив первое условие на второе, получим

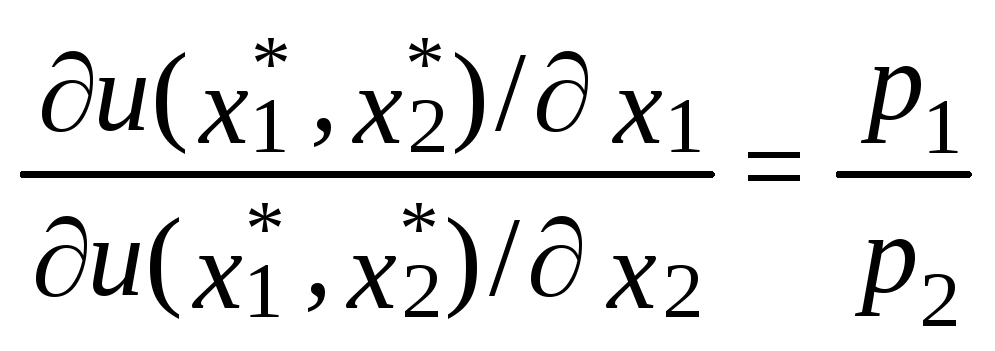81,

показывающее, как и раньше, что MRS должна равняться отношению цен. Другое уравнение дано бюджетным ограничением, так что у нас снова оказываются два уравнения с двумя неизвестными.

ПРИМЕР: Функции спроса Кобба — Дугласа

В главе 4 мы ввели функцию полезности Кобба — Дугласа

u(x₁, x₂) =82.

Поскольку функции полезности определимы лишь с точностью до монотонного преобразования, удобно прологарифмировать указанное выражение и работать далее с выражением

ln u(x₁, x₂) = c ln x₁ + d ln x₂.

Найдем функции спроса на x₁83 и x₂84 для функции полезности Кобба — Дугласа. Задача, которую мы хотим решить, имеет вид

max c ln x₁ + d ln x₂85

x₁, x₂ 86

при p₁x₁ + p₂x₂ = m87.

Существует по меньшей мере три способа решения этой задачи. Один из них — просто записать условие для MRS и бюджетное ограничение. Используя выражение для MRS, выведенное в гл. 4, получаем

,88

p₁x₁ + p₂x₂ = m89.

Это два уравнения с двумя неизвестными, решив которые, можно получить оптимальный выбор x₁90 и x₂91. Один из путей решения этих уравнений — подстановка второго уравнения в первое, которая дает

92.

Проделав перекрестное умножение, получим

c(m —x₁p₁) = dp₁x₁.

Преобразование данного уравнения дает

cm = (c + d) = p₁x₁ или

x₁ =93.

Это функция спроса на x₁94. Чтобы найти функцию спроса на x₂95, подставим полученное выражение в бюджетное ограничение и получим

x₂ =—96.

Второй путь решения — с самого начала подставить бюджетное ограничение в задачу на нахождение максимума. Если мы сделаем это, задача примет вид

max c ln x₁ + d ln (m/p₂ — x₁p₁/p₂).

x₁

Условие первого порядка для этой задачи имеет вид

—= 0.97

Немного несложных алгебраических преобразований и мы получаем решение

x₁ = 98

Подставив это выражение в бюджетное ограничение x₂ = m/p₂ — x₁p₁/p₂99, получим

100

Таковы функции спроса на два товара, к счастью, оказавшиеся теми же самыми, что и выведенные ранее другим методом.

Теперь обратимся к методу Лагранжа. Построим функцию Лагранжа

L = c ln x₁ + d ln x₂ — (p₁x₁ + p₂x₂ — m)

и продифференцируем ее, чтобы получить три условия первого порядка

—;101

—;102

—m = 0. 103

Фокус теперь состоит лишь в том, чтобы их решить! Лучше всего сначала найти решение для 104, а затем — дляx₁105 и x₂106. Преобразуем первые два уравнения и перекрестно их перемножим, получив в результате

c = p₁x₁, d = p₂x₂.107

Эти два уравнения так и хочется сложить:

c + d = (p₁x₁ + p₂x₂) = m,

что даст нам

108

Подставив это выражение обратно в первые два уравнения и выразив из них х₁109 и х₂110, получим, как и раньше,

.111

1 Не беспокойтесь, дальше мы получим некоторые не столь тривиальные результаты.