2.2. Динамика вращательного движения твердого тела

Рассмотрим произвольную механическую систему, состоящую из n материальных точек. Пусть - сила, действующая наi-ую материальную точку со стороны k-ой материальной точки, а - равнодействующая внешних сил, действующих наi-ую материальную точку системы. По второму закону Ньютона (см. (2.1.14)) уравнение движения материальной точки может быть представлено в виде: Причемтак какi-ая материальная точка на себя не действует. Умножим векторно - радиус-вектор, проведенный вi-ую материальную точку из начала координат, на уравнение движения материальной точки. Получим

(2.2.1,а)

Легко видеть, что из левой части выражения (2.2.1,а) можно вынести дифференциал . Действительно, так как(из определения векторного произведения), то. Таким образом,

.

(2.2.1,б)

Векторное произведение наназывают-моментом импульса i-ой материальной точки (в СИ единица измерения момента импульса - ):

(2.2.2)

Вектор перпендикулярен плоскости, где лежат вектораи, и образует с ними правую тройку векторов (рис. 2.1).

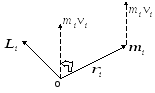
Рис. 2.1

Схематическое изображение вектора момента импульса i-ой материальной точки

Векторное произведение радиуса - вектора , проведенного в точку приложения силы, на эту силу, называетсямоментом силыотносительно точкиO (момент силы в системе СИ измеряют в ):

(2.2.3,а)

Векторы ,иобразуют правую тройку векторов:

Рис. 2.2.

Схематическое изображение вектора момента силы, действующего на i-ую материальную точку

Численное значение момента силы можно определить как:

Mi = Firisini = Fili,

(2.2.3,б)

где _i - угол между векторами и,l_i,= r_isin_i – длина перпендикуляра, опущенного из точки О на линию действия силы (плечо силы). Из уравнений (2.2.1,б), (2.2.2) и (2.2.3,а) следует, что:

(2.2.4,а)

Или для системы, состоящей из n точек:

…………………………………………..

(2.2.4,б)

Сложим почленно полученные выше уравнения:

(2.2.5)

Отметим, что суммарный вектор

(2.2.6)

называют главным моментом внешних сил относительно точки О, а вектор

(2.2.7,а)

моментом импульса системы материальных точек. Кроме того, очевидно

.

(2.2.7,б)

Для дальнейших выводов необходимо доказать, что

.

(2.2.8)

Действительно, по третьему закону Ньютона (2.1.9) . Как видно из рис.2.3,Следовательно, можно преобразовать(аналог третьего закона Ньютона во вращательном движении). Так как двойную сумму слева (2.2.8) можно разбить на сумму попарных слагаемых подобного вида , то и вся сумма в (2.2.8) тождественно равна нулю.

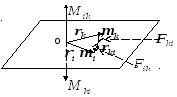
Рис. 2.3.

Взаимодействие i-ой и k-ой точек системы при вращении

относительно точки О

Таким образом, из выражений (2.2.6), (2.2.7,б) и (2.2.8) следует, что :

(2.2.9)

В соответствие с (2.2.9), скорость изменения момента импульса системы относительно неподвижной точки равна результирующему моменту (относительно той же точки) всех внешних сил, действующих на систему – основной закон динамики вращательного движения для системы материальных точек.

Рассмотрим случай, когда твердое тело закреплено в двух неподвижных точках O и O₁. В этом случае вращение тела можно рассматривать вокруг некоторой оси, например OZ. Такое вращение происходит под действием составляющей момента внешних сил . Из уравнения (2.2.9) следует, что:

(2.2.10)

Здесь , - составляющие векторов момента импульса тела и результирующего момента внешних сил относительно точки О, направленные вдоль неподвижной оси OZ вращения тела и называемые, соответственно, моментом импульса тела относительно оси OZ и главным моментом внешних сил относительно той же оси. Уравнение (2.2.10) является основным законом динамики для тела, вращающегося вокруг неподвижной оси.

Пусть тело, состоящее из n точек, вращается вокруг неподвижной оси с угловой скоростью Так как (из (2.2.7,а))тоИз рис. 2.4 следует, что для произвольнойi - ой точки Следовательно,Учтем, что вектор, являющийся результатом векторного произведения, перпендикулярен вектору(из определения векторного произведения), и проекция векторана осьOZ

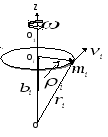
Рис. 2.4.

Схема вращательного движения твердого тела относительно оси OZ

Учтем, что (см. главу 1, п.2). В последнем случаеДляi - й точки , для всего тела окончательно

(2.2.11)

Сумму произведений масс материальных точек тела на квадрат расстояния от точек до оси вращения называют моментом инерции тела относительно этой оси (единицы измеренияв СИ -):

(2.2.12)

С учетом (2.2.12) уравнение (2.2.11) можно переписать в виде:

(2.2.13)

На практике при вычислении момента инерции тела его мысленно разбивают на бесконечно большое число малых элементов с массами dm и выражение (2.2.12) принимает вид:

Неподвижная ось вращения может проходить как через центр инерции тела, так и вне его. Докажем теорему о переносе осей инерции (теорема Штейнера): момент инерции тела I относительно произвольной оси ОО₁ равен сумме момента инерции тела I_C относительно оси O’O’₁, проведенной через центр инерции тела параллельно оси ОО₁ и произведения массы m тела на квадрат расстояния между этими осями (рис. 2.5):

I = IC + md2.

(2.2.14)

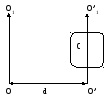
Рис. 2.5.

Схема вращательного движения тела относительно произвольной оси ОО₁

Доказательство: Согласно выражению (2.2.12) момент инерции тела относительно произвольной оси можно определить: , а относительно оси проходящей через центр масс -, где- расстояние отi-ой материальной точки тела до оси ОО₁; - расстояние от этой же точки до оси О’О’₁, проходящей через центр масс. Проведем ось OX таким образом, чтобы она пересекала оси ОО₁ и О’О’₁ , и была перпендикулярна им.

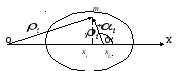
Рис.2.6.

Схема вращательного движения тела относительно произвольной оси OO₁ – вид сверху

Как видно из рис. 2.6, с учетом теоремы косинусов: причемгдеx_i и x_C – абсциссы i-ой точки тела и его центра инерции С. Преобразуем 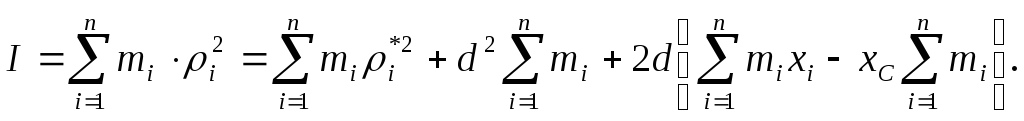Из определения центра инерции (см. (2.1.10,б))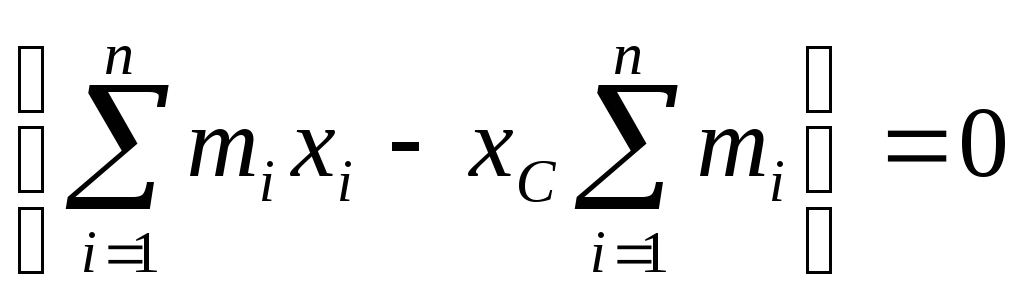. Таким образом,Что и требовалось доказать.

Таблица моментов инерции для однородных тел простейшей формы

№ п.п.	Тело	Положение оси OZ	Момент инерции I
1	Полый тонкостенный цилиндр радиусом R и массой m.	Ось симметрии
2	Сплошной цилиндр (диск) радиусом R и массой m.	Ось симметрии
3	Прямой тонкий стержень длиной l и массой m.	Ось перпендикулярная стержню и проходит через его середину
4	Прямой тонкий стержень длиной l и массой m.	Ось перпендикулярная стержню и проходит через его конец
5	Шар радиусом R и массой m.	Ось проходит через центр шара
6	Шар радиусом R и массой m.	Ось проходит на расстоянии d от центра шара

Из уравнения (2.2.13) следует, что основное уравнение динамики вращательного движения тела относительно неподвижной оси (2.2.10) можно записать в виде:

(2.2.15)

Если тело абсолютно твердое, то его момент инерции I_z не зависит от времени и, как следствие, , или

(2.2.16)

Из выражения (2.2.16) видно, что угловое ускорение твердого тела, вращающегося относительно неподвижной оси OZ, прямо пропорционально результирующему моменту (относительно этой оси) действующих на тело всех внешних сил, и обратно пропорционально моменту инерции тела относительно той же оси (второй закон Ньютона во вращательном движении). Таким образом, момент инерции является мерой инертности тела во вращательном движении.

В случае, когда ось вращения не закреплена, момент инерции тела не является скалярной величиной, а определяется матрицей, которую в физике называют тензором второго ранга:

.

В системе координат, состоящей из 3-х собственных векторов матрицы I , последняя приобретает диагональный вид

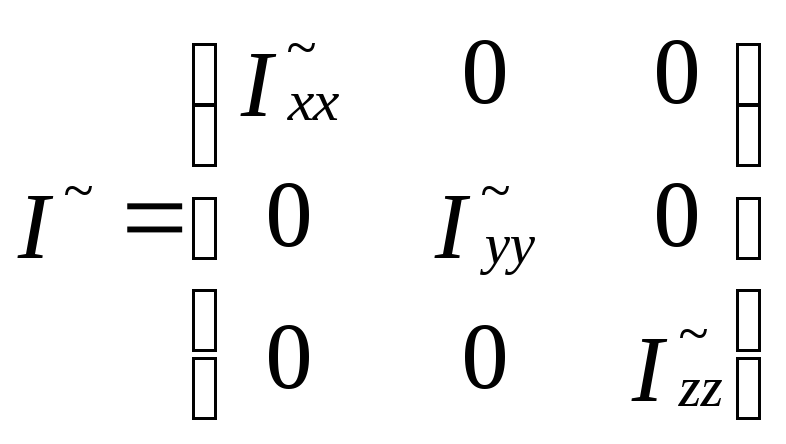
Диагональные элементы матрицы являютсясобственными числами матрицы I, и называются главными моментами инерции тела относительно главных осей – собственных векторов матрицы I. Как известно из курса высшей математики,

; .
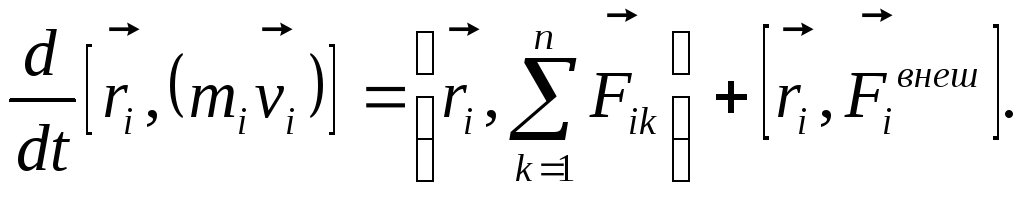