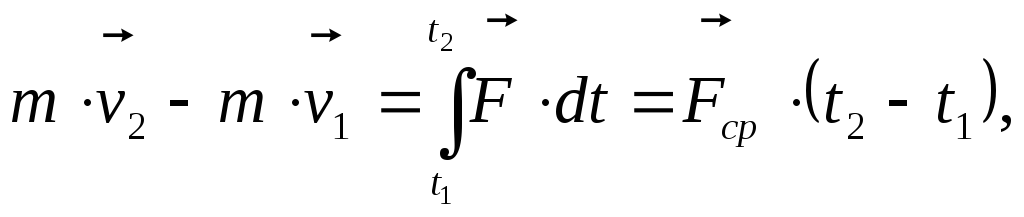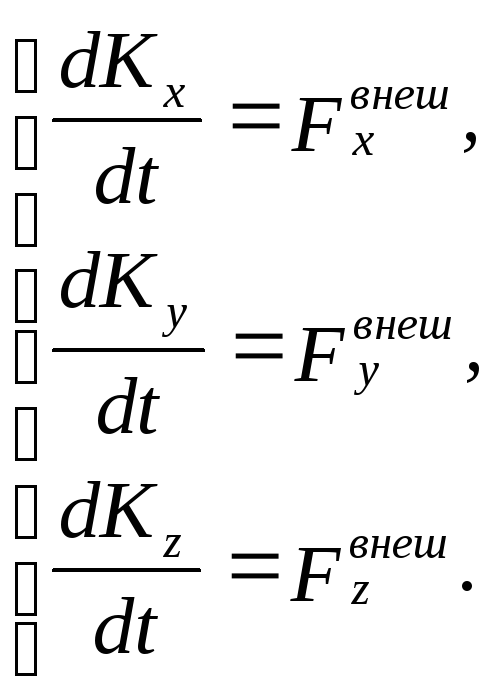Глава 2. Динамика
2.1. Динамика материальной точки и поступательного движения твердого тела
Первый закон Ньютона
В кинематике рассматривают механическое движение безотносительно к причинам и способам изменения самого движения. Задача динамики более общая – в ней изучают связь между взаимодействиями тел и законами их движения. Поэтому динамика представляет основной раздел механики. В основе динамики лежат три закона Ньютона.
Первый закон Ньютона гласит: всякое тело сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние. Первый закон Ньютона показывает, что состояния покоя или равномерного прямолинейного движения не требуют для своего поддержания каких-либо внешних воздействий. В этом проявляется особое динамическое свойство тел, называемое инертностью. Соответственно, первый закон Ньютона называют законом инерции, а движение тела, свободного от внешних воздействий – движением по инерции. Системы отсчета, по отношению к которым выполняется закон инерции, называются инерциальными системами отсчета. Таким образом, в первом законе Ньютона содержатся два утверждения: а) все тела обладают свойствами инертности; б) существуют инерциальные системы отсчета.
В приведенной выше формулировке первого закона Ньютона предполагается, что рассматриваемое тело – абсолютно твердое. Для других тел эта формулировка неприменима. Например, сжатая пружина после прекращения действия на нее внешних воздействий не покоится и не движется равномерно, а колеблется. Поэтому лучше пользоваться другой формулировкой первого закона Ньютона: материальная точка сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока воздействие со стороны других тел не выведет ее из этого состояния.
Сила
Для
описания механического действия тел
друг на друга вводят понятие силы. Силой,
действующей
на тело, называют физическую величину,
являющуюся мерой механического действия
на это тело со стороны какого-либо
другого тела. Сила - величина векторная.
Если на тело действуют одновременно n
сил
![]()
![]() …
…
![]() приложенных в одной и той же точке A
тела, то n
сил можно заменить одной силой
приложенных в одной и той же точке A
тела, то n
сил можно заменить одной силой
![]() ,
равной их геометрической сумме
,
равной их геометрической сумме
|
|
(2.1.1) |
![]() -
результирующая
или равнодействующая
сила. В
системе СИ единицей силы является ньютон
– Н.
-
результирующая
или равнодействующая
сила. В
системе СИ единицей силы является ньютон
– Н.
Масса. Второй закон Ньютона
Основная
задача динамики заключается в установлении
законов изменения механического движения
тел под влиянием приложенных к ним сил.
Эксперимент показывает, что под действием
силы
![]() свободное тело изменяет скорость своего
поступательного движения, приобретая
ускорение
свободное тело изменяет скорость своего
поступательного движения, приобретая
ускорение![]() При этом выполняется следующий закон:
При этом выполняется следующий закон:
|
|
(2.1.2,а) |
где
k1
– положительный коэффициент, постоянный
для данного тела, но не одинаковый для
разных тел. Из выражения (2.1.2,а) следует,
что тело обладает мерой
инертности
- под действием некоторой силы
![]() тело приобретает конечное ускорение
тело приобретает конечное ускорение![]() и, как следствие, скорость тела меняется
постепенно. В качестве меры инертности
тела в поступательном движении вводят
положительную скалярную величинуm,
называемую массой
тела. Чем
меньше инертность тела, тем больше
ускорение, приобретаемое телом под
действием силы, то есть
и, как следствие, скорость тела меняется
постепенно. В качестве меры инертности
тела в поступательном движении вводят
положительную скалярную величинуm,
называемую массой
тела. Чем
меньше инертность тела, тем больше
ускорение, приобретаемое телом под
действием силы, то есть
![]() и
и
|
|
(2.1.2,б) |
где k – коэффициент пропорциональности, который зависит от единиц измерения. Если все величины в (2.1.2,б) измеряются в одной системе единиц, то k = 1 и
|
|
(2.1.3) |
Таким
образом, из (2.1.3) следует, что ускорение
тела прямо пропорционально вызывающей
его силе (совпадает с ней по направлению),
и обратно пропорционально массе тела
– формулировка второго
закона Ньютона.
За основную единицу массы, называемую
килограммом
(кг), принимают массу эталонного тела,
хранящегося в международном бюро мер
и весов. Уравнение (2.1.3) описывает
изменение движения протяженного тела
под действием силы только при условии,
что тело: 1) не деформируется, и 2) движется
поступательно. В противном случае
ускорения разных точек тела неодинаковы,
и изменение движения всего тела (системы
материальных точек) нельзя описать с
помощью единого ускорения
![]() .
Для материальной точки условия 1) и 2)
всегда выполняются, и поэтому формулу
(2.1.3) называютосновным
уравнением динамики материальной точки.
Отметим, что из (2.1.3) следует первый закон
Ньютона. Действительно, если
.
Для материальной точки условия 1) и 2)
всегда выполняются, и поэтому формулу
(2.1.3) называютосновным
уравнением динамики материальной точки.
Отметим, что из (2.1.3) следует первый закон
Ньютона. Действительно, если
![]() ,
то
,
то![]() ,
что качественно соответствует формулировке
первого закона Ньютона. Разделение
первого и второго законов Ньютона
является исторически сложившемся
фактом.
,
что качественно соответствует формулировке
первого закона Ньютона. Разделение
первого и второго законов Ньютона
является исторически сложившемся
фактом.
Если
на материальную точку действуют несколько
сил, то
![]() где
где![]()
![]() (2.1.1):
(2.1.1):
|
|
(2.1.4) |
где
![]() - ускорение материальной точки,
приобретаемое под действием одной силы
- ускорение материальной точки,
приобретаемое под действием одной силы![]() .
Таким образом,если
на материальную точку одновременно
действуют несколько сил, то каждая из
них сообщает материальной точке такое
же ускорение, как если бы других сил не
было – формулировка
принципа
независимости действия сил.
.
Таким образом,если
на материальную точку одновременно
действуют несколько сил, то каждая из
них сообщает материальной точке такое
же ускорение, как если бы других сил не
было – формулировка
принципа
независимости действия сил.
Результирующую
силу
![]() ,
действующую на материальную точку,
всегда можно разложить на касательную
и нормальную составляющие к траектории
движения:
,
действующую на материальную точку,
всегда можно разложить на касательную
и нормальную составляющие к траектории
движения:![]() Аналогично для ускорения:
Аналогично для ускорения:![]() Из выражения (2.1.3) следует, что:
Из выражения (2.1.3) следует, что:![]()
![]() Отметим, что вектор силы
Отметим, что вектор силы![]() ,
как и ускорение
,
как и ускорение![]() ,
направлен к центру кривизны траектории,
и называетсяцентростремительной
силой. Так
как центростремительная сила всегда
перпендикулярна касательной к траектории
(то есть направлению вектора скорости),
то
,
направлен к центру кривизны траектории,
и называетсяцентростремительной
силой. Так
как центростремительная сила всегда
перпендикулярна касательной к траектории
(то есть направлению вектора скорости),
то![]() не меняет величины скорости, а меняет
только направление скорости материальной
точки:
не меняет величины скорости, а меняет
только направление скорости материальной
точки:
|
|
(2.1.5) |
Таким
образом, изменение модуля скорости v
определяется тангенциальной составляющей
результирующей силы
![]() .
Если
.
Если![]() то материальная точка движетсяускоренно,
то есть
то материальная точка движетсяускоренно,
то есть
![]() Если
Если![]() то материальная точка движетсязамедленно,
то есть
то материальная точка движетсязамедленно,
то есть
![]() При
При![]() =
0v
= const,
и если Fn
= const,
то радиус кривизны траектории движения
материальной точки можно определить
из выражения (2.1.5):
=
0v
= const,
и если Fn
= const,
то радиус кривизны траектории движения
материальной точки можно определить
из выражения (2.1.5):
![]() =const.
В указанном случае (
=const.
В указанном случае (![]() =
0,Fn
= const, R
= const)
материальная точка движется либо по
окружности (для плоского движения), либо
по винтовой линии (для движения в
пространстве).
=
0,Fn
= const, R
= const)
материальная точка движется либо по
окружности (для плоского движения), либо
по винтовой линии (для движения в
пространстве).
Импульс или количество движения материальной точки
Импульсом
или количеством
движения
материальной
точки
называется векторная величина, равная
произведению массы точки на ее скорость:
![]() (единица измерения в СИ -
(единица измерения в СИ -![]() ).
Отметим, что импульс является одной из
важнейших динамических характеристик,
зависящей как от быстроты движения
материальной точки, так и от ее инертности.
Используя выражение (1.1.9) можно показать,
что:
).
Отметим, что импульс является одной из
важнейших динамических характеристик,
зависящей как от быстроты движения
материальной точки, так и от ее инертности.
Используя выражение (1.1.9) можно показать,
что:![]() С другой стороны, согласно (2.1.3)
С другой стороны, согласно (2.1.3)![]() Следовательно
Следовательно
|
|
(2.1.6) |
Уравнение
(2.1.6) является одним из математических
выражений второго закона Ньютона:
скорость
изменения импульса материальной точки
равна силе, действующей на точку.
Из (2.1.6) следует, что
![]() где
где![]() -элементарный
импульс силы
за малый промежуток времени dt.
Таким образом, изменение импульса
материальной точки за малый промежуток
времени dt
равно элементарному импульсу результирующей
силы (за тот же промежуток времени),
действующей на материальную точку.
-элементарный
импульс силы
за малый промежуток времени dt.
Таким образом, изменение импульса
материальной точки за малый промежуток
времени dt
равно элементарному импульсу результирующей
силы (за тот же промежуток времени),
действующей на материальную точку.
Соответственно
изменение импульса материальной точки
за время от t
до t
+ t:
![]() -
импульс силы за это же время. Если
-
импульс силы за это же время. Если
![]() то
то![]() - линейная функция от времениt:
- линейная функция от времениt:
|
|
(2.1.7,а) |
где
v0
– начальная скорость материальной
точки (при t
= 0). При
![]()
![]() Из (2.1.7,а) следует, что за промежуток
времениt
= t2
- t1
Из (2.1.7,а) следует, что за промежуток
времениt
= t2
- t1
|
|
(2.1.7,б) |
Если
![]() то
то
|
|
(2.1.8) |
где
![]() -среднее
значение переменной силы
за промежуток времени t.
-среднее
значение переменной силы
за промежуток времени t.
Третий закон Ньютона. Движение центра инерции
Механическое воздействие двух тел друг на друга всегда представляет собой их взаимодействие, то есть, если тело 1 действует на тело 2, то при этом тело 2 в свою очередь действует на тело 1. На основе количественного анализа механического взаимодействия тел Ньютон установил свой третий закон динамики, который гласит: действия двух тел друг на друга всегда равны и направлены по одной прямой в противоположные стороны, то есть
|
|
(2.1.9) |
Здесь
![]() - сила, действующая на тело 1 со стороны
тела 2, а
- сила, действующая на тело 1 со стороны
тела 2, а![]() -
наоборот, соответственно. Третий закон
Ньютона является существенным дополнением
к первому и второму законам Ньютона.
-
наоборот, соответственно. Третий закон
Ньютона является существенным дополнением
к первому и второму законам Ньютона.
В динамике широко пользуются понятием центра инерции механической системы. Центром инерции или центром масс системы материальных точек называют такую точку C, радиус- вектор которой определяется следующим выражением:
|
|
(2.1.10,а) |
где
![]() и
и![]() - масса и радиус-векторi-ой
точки системы; m
– общая масса всей системы; n
– число материальных точек в системе.
Соответственно декартовые компоненты
центра масс
- масса и радиус-векторi-ой
точки системы; m
– общая масса всей системы; n
– число материальных точек в системе.
Соответственно декартовые компоненты
центра масс
![]() равны:
равны:
|
|
(2.1.10,б) |
Напомним
из школьной программы, что центром
тяжести системы
называют точку приложения равнодействующей
параллельных сил тяжести всех частей
системы. Радиус - вектор центра тяжести
равен:
![]()
![]() - численное значение силы тяжестиi-ой
материальной точки, то есть
- численное значение силы тяжестиi-ой
материальной точки, то есть
![]()
![]() гдеg
– ускорение свободного падения. Поэтому
гдеg
– ускорение свободного падения. Поэтому
![]()
![]() Таким образом центр тяжести системы
совпадает с центром масс.
Таким образом центр тяжести системы
совпадает с центром масс.
Найдем скорость движения центра инерции системы:
|
|
(2.1.11) |
Геометрическую
сумму импульсов всех материальных точек
системы называют импульсом
системы
![]() :
:![]() Следовательно, из (2.1.11)
Следовательно, из (2.1.11)
|
|
(2.1.12) |
Тела,
не входящие в состав рассматриваемой
механической системы, называют внешними,
а силы, действующие на систему со стороны
этих тел – внешними
силами. Силы
взаимодействия между телами системы
называют внутренними
силами. Если
![]() -
сила, действующая наi-ую
материальную точку со стороны k-ой,
то результирующая со стороны всех
внутренних сил, приложенных к i-ой
точке, равна:
-
сила, действующая наi-ую
материальную точку со стороны k-ой,
то результирующая со стороны всех
внутренних сил, приложенных к i-ой
точке, равна:
|
|
(2.1.13) |
В
(2.1.13) k
пробегает значения от 1 до n,
кроме i,
так как i-ая
точка не может действовать сама на себя.
Пусть на i-ую
материальную точку действует внешняя
сила
![]() ,
при этом по второму закону Ньютона
(2.1.6) для системы материальных точек
можно записать следующие уравнения:
,
при этом по второму закону Ньютона
(2.1.6) для системы материальных точек
можно записать следующие уравнения:
|
…………………………………………..
|
(2.1.14) |
Складывая
почленно уравнения (2.1.14), и группируя
попарно силы
![]() и
и![]() ,
можно получить:
,
можно получить:![]() Согласно третьему закону Ньютона (2.1.9)
Согласно третьему закону Ньютона (2.1.9)![]() и,
как следствие,
и,
как следствие,![]()
![]() - называютглавным
вектором внешних сил.
С другой стороны,
- называютглавным
вектором внешних сил.
С другой стороны,![]() ,
то есть
,
то есть
|
|
(2.1.15,а) |
Уравнение (2.1.15,а) называют основным уравнением динамики поступательного движения системы материальных точек, которое показывает, что скорость изменения импульса механической системы равна главному вектору всех внешних сил, действующих на эту систему. В проекциях на декартовые оси выражение (2.1.15,а) примет вид:
|
|
(2.1.15,б) |
В
(2.1.15,б)
![]()
![]()
![]() С помощью уравнения (2.1.12) можно переписать
(2.1.15,а)
С помощью уравнения (2.1.12) можно переписать
(2.1.15,а)
|
|
(2.1.16) |
где
![]() -ускорение
центра инерции.
Таким образом, центр
инерции механической системы движется
как материальная точка, масса которой
равна массе всей системы, и на которую
действует сила, равная главному вектору
внешних сил, приложенных к системе.
-ускорение
центра инерции.
Таким образом, центр
инерции механической системы движется
как материальная точка, масса которой
равна массе всей системы, и на которую
действует сила, равная главному вектору
внешних сил, приложенных к системе.
В общем случае движение твердого тела можно рассматривать как сумму двух движений: 1) поступательного со скоростью, равной скорости центра масс, и 2) вращательного вокруг центра инерции (С). Поэтому уравнение (2.1.16) часто называют основным уравнением динамики поступательного движения твердого тела.
Закон сохранения импульса
Механическую систему называют замкнутой или изолированной, если на нее не действуют внешние силы, то есть если она не взаимодействует с внешними телами. Для замкнутой системы главный вектор внешних сил тождественно равен нулю. Поэтому из выражения (2.1.15,а) следует закон, который называют законом сохранения импульса: импульс замкнутой системы не изменяется с течением времени, то есть
|
|
(2.1.17) |
где
![]() и
и![]() - масса и скоростьi-ой
материальной точки системы. Так как из
(2.1.12) известно, что
- масса и скоростьi-ой
материальной точки системы. Так как из
(2.1.12) известно, что
![]() то, используя уравнение (2.1.17), можно
показать, что при любых процессах,
происходящих в замкнутой системе,
скорость ее центра инерции сохраняется
неизменной.
то, используя уравнение (2.1.17), можно
показать, что при любых процессах,
происходящих в замкнутой системе,
скорость ее центра инерции сохраняется
неизменной.
Если
система не замкнута, но главный вектор
внешних сил
![]() ,
то уравнение (2.1.17) справедливо и в
открытой системе. Обычно приходится
иметь дело с незамкнутыми системами,
для которых
,
то уравнение (2.1.17) справедливо и в
открытой системе. Обычно приходится
иметь дело с незамкнутыми системами,
для которых![]() и, как следствие,
и, как следствие,![]() Однако если проекция главного вектора
внешних сил на какую-либо ось, неподвижную
относительно инерциальной системы
отсчета, тождественно равна нулю, то
проекция на эту же ось вектора импульса
системы не зависит от времени. Например,
если
Однако если проекция главного вектора
внешних сил на какую-либо ось, неподвижную
относительно инерциальной системы
отсчета, тождественно равна нулю, то
проекция на эту же ось вектора импульса
системы не зависит от времени. Например,
если
![]() = 0, то
= 0, то![]() и, следовательно, Kx
= const – закон
сохранения проекции импульса.
и, следовательно, Kx
= const – закон
сохранения проекции импульса.
Рассмотрим
применение закона сохранения импульса
(2.1.17) на примере удара двух тел. Ударом
называется явление изменения скорости
тел на конечные величины за очень малый
промежуток времени, происходящее при
столкновении тел. Общую нормаль к
поверхностям соударяющихся тел в точке
их соприкосновения называют линией
удара. Удар
называют прямым,
если перед ударом скорости центров
инерции соударяющихся тел параллельны
линии удара. Удар называют центральным,
если центры инерции соударяющихся тел
лежат на линии удара. Прямой центральный
удар называют абсолютно
неупругим,
если после удара тела движутся как одно
целое. Если скорости двух тел до удара
соответственно равны –
![]() и
и
![]() ,
а массы их определяются значениями m1
и m2,
то согласно уравнению (2.1.17) общая скорость
тел после абсолютно неупругого удара
,
а массы их определяются значениями m1
и m2,
то согласно уравнению (2.1.17) общая скорость
тел после абсолютно неупругого удара
![]() может быть представлена в виде:
может быть представлена в виде:
|
|
(2.1.18) |