1 СЕМЕСТР. Информатика. Темы всех занятий 1-15 .rar / т_тема 8

Тема 8. ФОРМАЛЬНАЯ ЛОГИКА. ИСПОЛЬЗОВАНИЕ АЛГЕБРЫ ЛОГИКИ ДЛЯ ФОРМАЛИЗАЦИИ ФАРМАЦЕВТИЧЕСКИХ ЗАДАЧ

Логика очень древняя наука. Ещё в античные времена была известна формальная логика, позволяющая делать заключения о правильности какого-либо суждения не по его фактическому содержанию, а только по форме его построения.

Формальная логика - конструирование и исследование правил преобразования высказываний, сохраняющих их истинное значение безотносительно к содержанию входящих в эти высказывания понятий. Формальная логика, в отличие от неформальной, организована как формальная система, обладающая высоким уровнем абстракции и чётко определёнными методами, правилами и законами.

Формальная логика как наука занимается выводом нового знания на основе ранее известного без обращения в каждом конкретном случае к опыту, а применением законов и правил мышления.

Первым законом формальной логики, который был известен еще в древности, был закон исключения третьего. Примером его содержательной трактовки можно использовать следующую фразу: «Во время своих странствований Платон был в Египте ИЛИ не был в Египте». Ничего другого быть не может: Платон либо был, либо не был в Египте - третьего не дано.

Второй закон формальной логики - закон непротиворечивости – утверждает, что, если из теории следуют два противоречащих друг другу вывода, то такая теория, безусловно, неправильная (ложная) и должна быть отвергнута. Очевидно, что следующая фраза: «Во время своих странствий Платон был в Египте И не был в Египте», ложна.

Третий закон формальной логики - закон отрицания. Примером его использования может служить следующая фраза: «Если НЕ верно, что Платон НЕ был в Египте, то значит, Платон был в Египте».

Формальная логика основана на высказываниях.

Высказывание - основной элемент логики, определяемый как повествовательное предложение, относительно которого можно однозначно сказать, истинное или ложное утверждение оно содержит.

Например:

1. «Препарат Линекс применяют при нарушении равновесия микрофлоры кишечника.»

2. «Актовегин используют в лечении пневмонии.»

Первое высказывание истинно, второе - ложно. Вопросительное, побудительное и восклицательное предложения не являются высказываниями, так как в них ничего не утверждается и не отрицается.

Примеры предложений, не являющихся высказываниями: «Не используйте лекарственные средства без назначения врача!» Кто не хочет быть здоровым?

Высказывания могут быть и такими: 2>1, Н₂О+SO₃=H₂SO₄. В данном случае используются языки математических символов и химических формул.

Приведенные выше примеры высказываний являются простыми. Из простых высказываний можно получить сложные, объединив их с помощью логических связок. “И”, “ИЛИ”, “НЕ”, “ЕСЛИ ... ТО”. В рассмотренных нами трёх законах формальной логики использовались связки “ИЛИ”, “И”, “НЕ”.

В 1847 году английский математик Джордж Буль разработал алгебру логики.

Алгебра логики очень проста, так как каждая переменная может принимать только два значения: истинно или ложно, которые могут быть заменены символами 1 и 0 соответственно.

Основные логические функции (операции), используемые в алгебре логики.

Результат выполнения логической функции принято задавать в виде таблицы истинности. В столбцах такой таблицы перечисляются все возможные значения аргументов функции (А, В) и указываются соответствующие им значения логической функции.

1. Логическая операция НЕ (логическое отрицание или инверсия). Таблица истинности для этой функции имеет вид:

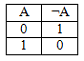
2. Логическая операция И (логическое умножение, конъюнкция). Таблица истинности для этой функции имеет вид:

3. Логическая операция ИЛИ (логическое сложение, дизъюнкция). Таблица истинности имеет вид:

Набор логических функций НЕ, И, ИЛИ является базисом алгебры логики. С помощью него можно выразить другие логические функции, например, операции “импликации”, “эквивалентности” и др.

Рассмотрим некоторые из них.

4. Логическая операция “импликация”. Функция ЕСЛИ … ТО. Таблица истинности для этой функции имеет вид:

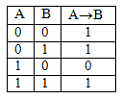
Операцию “импликация” обозначают:

Операция “импликация” выражается через логические функции ИЛИ, НЕ в виде логической формулы

5. Логическая операция “эквивалентность” (равнозначность). Этой логической операции соответствует логическая функция ЕСЛИ И ТОЛЬКО ЕСЛИ, «тогда и только тогда». Таблица истинности для этой функции имеет вид:

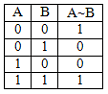
Говорят, что значение А эквивалентно В, если и только если они равнозначны. Логическая операция “эквивалентность” выражается через логические функции И, ИЛИ, НЕ в виде логической формулы

С помощью алгебры логики законы формальной логики могут быть записаны следующим образом.

В алгебре логики справедливы следующие законы: переместительный (закон коммутативности), сочетательный (закон ассоциативности) и распределительный (закон дистрибутивности), применение которых позволяет производить упрощение логических функций, т.е. находить для них выражения, имеющие наиболее простую форму.

Использование логических функций среды табличного процессора для проведения расчетов в фармации

Логические функции являются неотъемлемым компонентом многих формул. Всякий раз, когда необходимо реализовать те или иные действия в зависимости от выполнения каких-либо условий, следует использовать логические функции

Логических функций в Excel шесть. Их описание приводится полностью. 

Функция ЕСЛИ

Синтаксис:

ЕСЛИ (лог_выражение, значение_если_истина, значение_если_ложь)

Результат: Возвращает одно значение, если аргумент лог_выражение при вычислении дает значение ИСТИНА, и другое значение, если ЛОЖЬ. Функция ЕСЛИ используется для проверки значений формул и организации переходов в зависимости от результатов этой проверки. Результат проверки определяет значение, возвращаемое функцией ЕСЛИ.

Аргументы:

• лог_выражение - любое значение или выражение, которое при вычислении дает значение ИСТИНА или ЛОЖЬ;

• значение_если_истина - значение, которое возвращается, если аргумент лог_выражение - имеет значение ИСТИНА; если аргумент лог_выражение имеет значение ИСТИНА и аргумент значение_если_истина опущен, то возвращается значение ИСТИНА;

• значение_если_ложь - значение, которое возвращается, если аргумент лог_выражение имеет значение ЛОЖЬ. Если аргумент лог_выражение имеет значение ЛОЖЬ и аргумент значение_если_ложь опущен, то возвращается значение ЛОЖЬ.

ПРИМЕЧАНИЕ

Может быть вложено до семи условий ЕСЛИ;

Функция И

Синтаксис:

И (логическое_значение1,логическое_значение2,...)

Результат: Возвращает значение ИСТИНА, если все аргументы имеют значение ИСТИНА; возвращает значение ЛОЖЬ, если хотя бы один аргумент имеет значение ЛОЖЬ.

Аргументы:

• логическое_значение1,логическое_значение2,... - от 1 до 30 проверяемых условий, которые могут иметь значение либо ИСТИНА, либо ЛОЖЬ. Аргументы должны быть логическими значениями, массивами или ссылками, которые содержат логические значения. Если аргумент, который является ссылкой или массивом, содержит тексты или пустые ячейки, то такие значения игнорируются. Если указанный интервал не содержит логических значений, то функция И возвращает значение ошибки #ЗНАЧ!.

Функция ИЛИ

Синтаксис:

ИЛИ (логическое_значение1,логическое значение2,...)

Результат: Возвращает значение ИСТИНА, если хотя бы один из аргументов имеет значение ИСТИНА; возвращает значение ЛОЖЬ, если все аргументы имеют значение ЛОЖЬ.

Аргументы:

• логическое_значение1,логическое_значение2,... - от 1 до 30 проверяемых условий, которые могут иметь значение либо ИСТИНА, либо ЛОЖЬ. Можно использовать функцию ИЛИ как формулу массива, чтобы проверить, имеются ли значения в массиве. Для того чтобы ввести функцию ИЛИ как формулу массива, нажмите клавиши [Ctrl+Shift].

Функция ИСТИНА

Синтаксис:

ИСТИНА()

Результат: Логическое значение ИСТИНА.

Аргументы: Нет. 

Функция ЛОЖЬ

Синтаксис:

ЛОЖЬ()

Результат: Логическое значение ЛОЖЬ.

Аргументы: Нет. 

Функция НЕ

Синтаксис:

НЕ (логическое_значение)

Результат: Заменяет логическое значение аргумента на противоположное. Функция НЕ используется в тех случаях, когда необходимо иметь уверенность в том, что значение не равно некоторой конкретной величине.

Аргументы:

• логическое_значение - значение или выражение, которое при вычислении дает значение ИСТИНА или ЛОЖЬ. Если аргумент логическое_значение - имеет значение ЛОЖЬ, то функция НЕ возвращает значение ИСТИНА; если аргумент логическое^значение имеет значение ИСТИНА, то функция НЕ возвращает значение ЛОЖЬ.

Вложенные функции ЕСЛИ

Иногда бывает очень трудно решить логическую задачу только с помощью операторов сравнения и функций И, ИЛИ, НЕ. В этих случаях можно использовать вложенные функции ЕСЛИ. Например, в следующей формуле используются три функции ЕСЛИ:

=ЕСЛИ(А1=100;"Всегда";ЕСЛИ(И(А1>=80;А1<100);"Обычно";ЕСЛИ(И(А1>=60;А1<80);"Иногда";"Никогда")))

Если значение в ячейке А1 является целым числом, формула читается следующим образом: "Если значение в ячейке А1 равно 100, возвратить строку "Всегда". В противном случае, если значение в ячейке А1 находится между 80 и 100, возвратить "Обычно". В противном случае, если значение в ячейке А1 находится между 60 и 80, возвратить строку "Иногда". И, если ни одно из этих условий не выполняется, возвратить строку "Никогда". Всего допускается до 7 уровней вложения функций ЕСЛИ.

Функция ЕПУСТО

Если нужно определить, является ли ячейка пустой, можно использовать функцию ЕПУСТО (ISBLANK), которая имеет следующий синтаксис:

=ЕПУСТО(значение)

Аргумент значение может быть ссылкой на ячейку или диапазон. Если значение ссылается на пустую ячейку или диапазон, функция возвращает логическое значение ИСТИНА, в противном случае ЛОЖЬ.