Раздел V. Элементы квантовой физики атомов, молекул

И ТВЕРДЫХ ТЕЛ

Основные законы и формулы

• Длина волны де Бройля

где постоянная Планка,

импульс частицы.

• Соотношение неопределенностей Гейзенберга:

для координаты и импульса ,

где неопределенность координаты частицы,

неопределенность проекции импульса частицы на ось;

для энергии и времени

где неопределенность энергии частицы в некотором состоянии,

время нахождения частицы в этом состоянии.

• Плотность вероятности нахождения частицы в некотором месте

где волновая функция частицы.

• Волновая функция, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме

где ширина ямы,

координата частицы в яме (),

квантовое число ().

• Энергия частицы в бесконечно глубокой одномерной потенциальной яме

где масса частицы.

• Сериальные формулы спектра водородоподобных атомов

где длина волны спектральной линии,

постоянная Ридберга,

порядковый номер элемента,

• Спектральные линии характеристического рентгеновского излучения

где постоянная экранирования.

• Дефект массы ядра

где масса протона,

масса нейтрона,

масса атома ,

и масса атома и его ядра,

и зарядовое и массовое числа.

• Энергия связи ядра

где скорость света.

• Удельная энергия связи

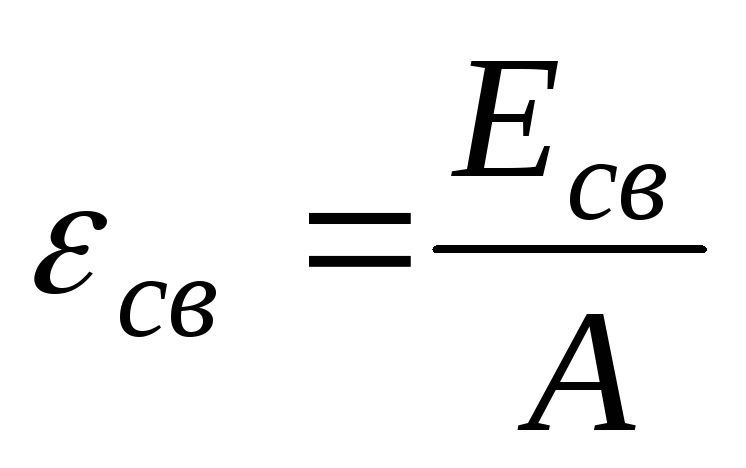
• Закон радиоактивного распада

где начальное число радиоактивных ядер в момент времени,

число нераспавшихся радиоактивных ядер в момент времени ,

постоянная радиоактивного распада.

• Активность радиоактивного вещества

• Энергия ядерной реакции

где имассы покоя частиц, вступивших в реакцию,

сумма масс покоя частиц, образовавшихся в результате реакции.

• Закон поглощения излучения веществом

где интенсивность излучения на входе в поглощающий слой вещества,

интенсивность излучения после прохождения слоя толщиной ,

линейный коэффициент поглощения.

Таблица вариантов

Номер студента по списку	Номера задач
1, 11, 21, 31 2, 12, 22, 32 3, 13, 23, 33 4, 14, 24, 34 5, 15, 25, 35 6, 16, 26, 36 7, 17. 27, 37 8, 18, 28, 38 9, 19, 29, 39 10, 20, 30, 40	1 2 3 4 5 6 7 8 9 10	11 12 13 14 15 16 17 18 19 20	21 22 23 24 25 26 27 28 29 30	31 32 33 34 35 36 37 38 39 40	41 42 43 44 45 46 47 48 49 50

Примеры решения задач

Пример 1. Атом водорода испустил фотон с длинной волны 4,86 10^-7 м. На сколько изменилась энергия электрона в атоме?

Решение. По теории Бора при переходе электрона из состояния с энергией в состояние с энергиейизлучается фотон с энергией, равной.

Учитывая, что , получаем

, .

Ответ: .

Пример 2. Вычислить длину волны де Бройля электрона, движущегося со скоростью 0,75с (с – скорость света).

Решение. Длина волны де Бройля . Импульс частицы, движущейся с релятивистской скоростью, равен.

Тогда

;

.

Ответ: .

Пример 3. Вычислить дефект массы, энергию связи и удельную энергию связи ядра .

Решение. Дефект массы ядра определяется по формуле

,

или

,

где масса атома, дефект массы ядра которого определяется.

Подставляя в последнее выражение числовые данные, получим

Энергия связи ядра определяется по формуле

.

Если дефект массы выражать в а. е. м., а энергию связи в МэВ, то последняя формула примет вид

.

Подставляя числовые значения, получим

.

Удельная энергия связи вычисляется по формуле

.

Проводя вычисления, получим

.

Ответ: ,,.

Пример 4. За год распалось 60% некоторого исходного радиоактивного элемента. Определить период полураспада этого элемента.

Решение. Закон радиоактивного распада имеет вид

,

где исходное число радиоактивных ядер,число нераспавшихся ядер к моменту времени,постоянная распада, которая связана с полупериодом распада соотношением. По условию задачи

;

; ;;.

Тогда

.

Ответ: .

Пример 5. Вычислить энергию ядерной реакции . Выделяется или поглощается энергия при этой реакции?

Решение. Энергия ядерной реакции определяется по формуле

.

где имассы частиц, вступивших в реакцию,сумма частиц, образовавшихся в результате реакции.

Если массу частиц выражать в а. е. м., а энергию реакции в МэВ, то последняя формула примет вид

.

При вычислении энергии ядерной реакции можно использовать массы атомов вместо масс их ядер.

Дефект массы реакции равен

Энергия ядерной реакции равна

.

Поскольку , то энергия в результате реакции поглощается.

Ответ: , энергия поглощается.