
|
Кафедра математики и информатики |
Теория игр |
|
Методические указания по выполнению контрольных работ |
Светлова Н.И. |
|
Утверждено протоколом заседания кафедры |
|
|
Направление: |
Экономика | |
|
Форма обучения: |
заоч |
заоч |
|
Срок обучения: |
5 лет |
3,5 г |
|
Семестр: |
|
3 |
1 Задачи теории игр
Если имеется несколько конфликтующих сторон (лиц), каждая из которых принимает некоторое решение, определяемое заданным набором правил, и каждому из лиц известно конечное состояние конфликтной ситуации с заранее определенными для каждой из сторон платежами, то говорят, что имеет место игра.
Задача теории игр состоит в выборе такой линии поведения данного игрока, отклонение от которой может лишь уменьшить его выигрыш.
Некоторые определения игры
Количественная оценка результатов игры называется платежом.
Парная игра(два лица) называется игрой с нулевой суммой, если сумма платежей равна нулю, т.е. если проигрыш одного игрока равен выигрышу другого.
Однозначное описание выбора игрока в каждой из возможной ситуаций, при которой он должен сделать личный ход, называется стратегией игрока.
Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает игроку максимально возможный средний выигрыш (или, что - то же самое, минимально возможный средний выигрыш).
Игра, определяемая матрицей А, имеющейmстрок иnстолбцов, называется конечной парной игрой размерностиm*n;
 (1.1)
(1.1)
где
i=![]() - стратегия первого игрока, имеющегоmстратегий; j=
- стратегия первого игрока, имеющегоmстратегий; j=![]() - стратегия второго игрока, имеющегоnстратегий;
- стратегия второго игрока, имеющегоnстратегий;
![]() ij
– выигрыш первого игрока поi-й
стратегии при использовании вторымj-й
стратегии (или, что то же самое, проигрыш
второго по своейj-й
стратегии, при использовании первымi-й);
ij
– выигрыш первого игрока поi-й
стратегии при использовании вторымj-й
стратегии (или, что то же самое, проигрыш
второго по своейj-й
стратегии, при использовании первымi-й);
А = ij– платежная матрица игры.
1.1 Игра с чистыми стратегиями
Нижняя цена игры (для игрока первого)
= max (min ij ). (1.2)
i j
Верхняя цена игры (для второго игрока):
![]() = min
(maxij)
. (1.3)
= min
(maxij)
. (1.3)
J i
Если = , игра называется с седловой точкой (1.4), или игра с чистыми стратегиями. При этомV = = называют ценной игры (V- цена игры).
Пример.Дана платежная матрица игры 2 лиц А. Определить оптимальные стратегии для каждого из игроков и цену игры:
min max
j i
 (1.4)
(1.4)
 max
10 9 12 6
max
10 9 12 6
i
min 6
j
![]() - стратегия первого
игрока (строки).
- стратегия первого
игрока (строки).
![]() -
стратегия второго игрока (столбцы).
-
стратегия второго игрока (столбцы).
![]() - цена игры.
- цена игры.
Таким образом, игра имеет седловую точку. Стратегия j = 4 – оптимальная для второго игрока, стратегияi=2 - для первого. Имеем игру с чистыми стратегиями.
1.2 Игры со смешанными стратегиями
Если платежная
матрица не имеет седловой точки, т.е.
![]() ,
и ни один из участников игры не может
выбрать один план в качестве своей
оптимальной стратегии, игроки переходят
на «смешанные стратегии». При этом
каждый из игроков использует в процессе
игры несколько раз каждую из своих
стратегий.
,
и ни один из участников игры не может
выбрать один план в качестве своей
оптимальной стратегии, игроки переходят
на «смешанные стратегии». При этом
каждый из игроков использует в процессе
игры несколько раз каждую из своих
стратегий.
Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называется смешанной стратегией данного игрока.
Х = (х1…хi…хm) – смешанная стратегия первого игрока.
У= (у1…уj…уn) – смешанная стратегия второго игрока.
x i,
уj– относительные
частоты (вероятности) использования
игроками своих стратегий.
i,
уj– относительные
частоты (вероятности) использования
игроками своих стратегий.
Условия использования смешанных стратегий
![]() .
(1.5)
.
(1.5)
Если Х* = (х1*….хi*…хm*) – оптимальная стратегия, выбранная первым игроком;Y* = (у1*…уj*…уn*) – оптимальная стратегия, выбранная вторым игроком, то число является ценой игры.
 (1.6)
(1.6)
Для того чтобы число Vбыло ценой игры, ах* иу* - оптимальными стратегиями, необходимо и достаточно выполнение неравенств
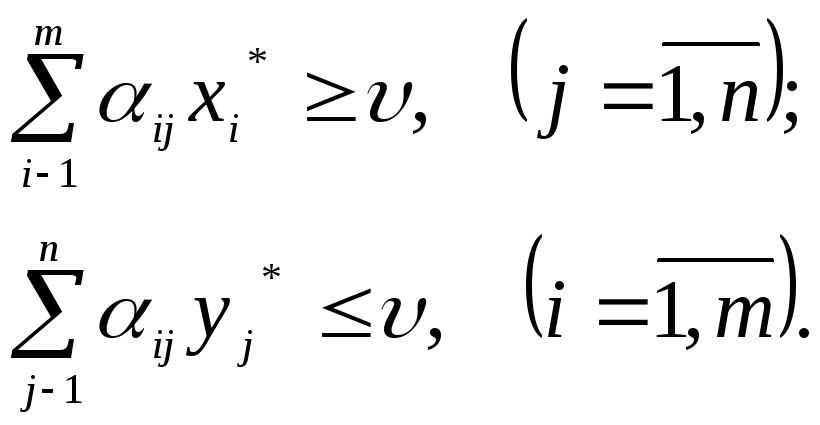 (1.7)
(1.7)
Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры Vвне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную, в том числе и чистые стратегии.
Сведения задач теории игр к задачам линейного программирования.
Пример. Найти решение игры, определяемой платежной матрицейА.
А =
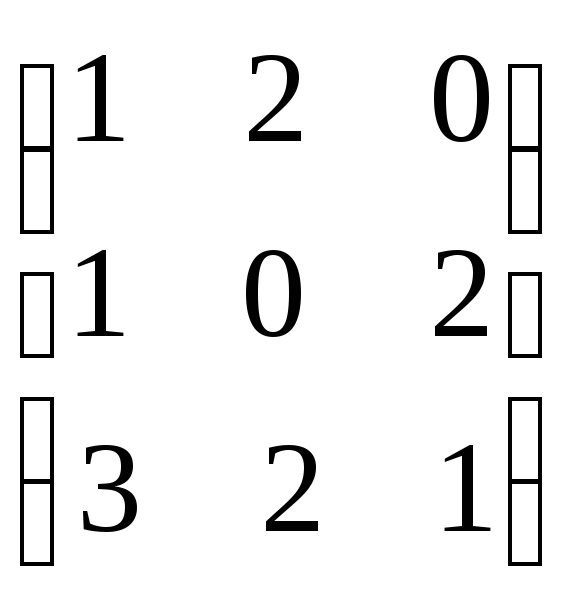
![]() (1.8)
(1.8)
y1 y2 y3
Решение:
Составим двойственную пару задач линейного программирования.
Для первого игрока
 (1.9)
(1.9)
у1 +у2 +у3 = 1 (1.10)
Освобождаясь от переменной V(цена игры), разделим левую и правую часть выражений (1.9), (1.10) наV. Принявуj /Vза новую переменнуюzi, получим новую систему ограничений (1.11) и целевую функцию (1.12)
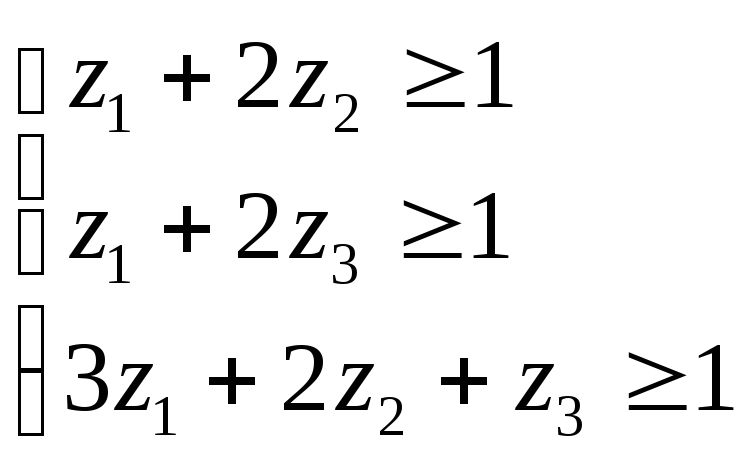 (1.11)
(1.11)
![]() .
(1.12)
.
(1.12)
Аналогично получим модель игры для второго игрока:
 (1.13)
(1.13)
х1 +х2 +х3 = 1 . (1.14)
Приведя модель (1.13), (1.14) к форме без переменной V, получим
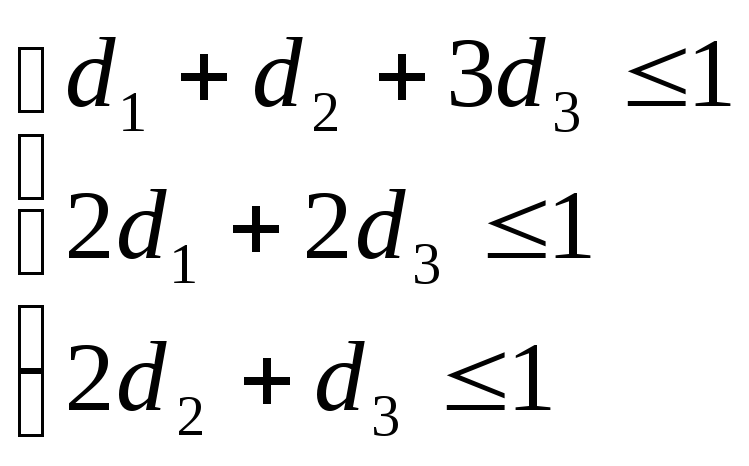 (1.15)
(1.15)
![]() ,
(1.16)
,
(1.16)
где
 .
.
Если нам необходимо определить стратегию поведения первого игрока, т.е. относительную частоту использования его стратегий (х1….хi…хm), мы будем использовать модель второго игрока, т.к. эти переменные находятся в его модели выигрыша (1.13), (1.14).
Приведем (1.15), (1.16) к канонической форме
 (1.17)
(1.17)
![]() .
(1.18)
.
(1.18)
Дальше задача (1.17), (1.18) решается симплекс – методом (табл.1.1)
Базисное решение:
d1= 1/2;d2= 1/2;d3= 0;d4= 0;d5= 0;d6= 0.
Цена игры:
![]()
Исходные параметры, относительные частоты применения стратегий
![]()
x3 = 0;x4 = 0;x5 = 0;x6 = 0;
x2 =d2V= 1/21 = 1/2.
Для проведения стратегий второго игрока используется модель игры первого: (1.9), (1.10), (1.11), (1.12).
Таблица 1.1
-
Б
d1 d2 d3 d4 d5 d6
св. чл
bj / aij
d4
1 d5
d6
1 1 3 1 0 0
2
 0 2 0 1 0
0 2 0 1 00 2 1 0 0 1
I
I
I
1/2

-
 1
-1 -1 0 0 0
1
-1 -1 0 0 00
d4
2 d5
d2
1 0 5/2 1 0 -1/2
2 0 2 0 1 0
0 1 1/2 0 0 1/2
1/2
1
1/2
1/2

-1 0 -1/2 0 0 1/2
1/2
d1
3 d5
d2
1 0 5/2 1 0 -1/2
0 0 -3 -2 1 1
0 1 1/2 0 0 1/2
1/2
0
1/2

0 0 2 1 0 0
1
