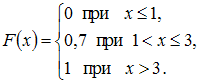математика
.doc
Определитель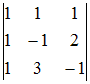 
после
приведения к треугольному виду можно
записать как …
Даны
матрицы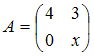 
, 
, 
.
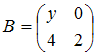Если выполняется равенство 
,
то 
равно
…
|
|
|
1 |
Даны
матрицы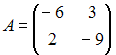 
и .
Тогда 
…
|
|
равно |
Ранг
матрицы 
равен
единице при 
,
равном …
|
|
10 |
Если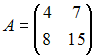 
,
то обратная к ней матрица 
равна
…
|
|
|
|
Если
система линейных уравнений
,
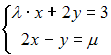где 
–
некоторые числа,
имеет бесконечное
множество решений, то 
равно
…
|
|
|
6 |
Точка
В симметрична точке 
относительно
оси абсцисс. Тогда расстояние между
точками А и В равно …
|
|
|
4 |
В
полярных координатах уравнение прямой,
проходящей через полюс под углом 
к
полярной оси, имеет вид …
|
|
|
|
Дано
уравнение прямой в виде 
.
Тогда уравнение этой прямой «в отрезках»
имеет вид …
|
|
|
|
Уравнение
окружности с центром в точке 
и
радиусом 
имеет
вид …
|
|
|
|
Дано
общее уравнение плоскости 
.
Тогда уравнение этой плоскости «в
отрезках» имеет вид …
|
|
|
|
Координаты
центра эллипсоида 
равны
…
|
|
|
|
Область
определения функции 
имеет
вид …
|
|
|
|
Предел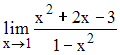 
равен
…
|
|
|
– 2 |
Количество
точек разрыва функции 
равно
…
|
|
|
1 |
Производная
функции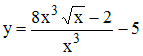 
равна
…
|
|
|
|
Производная
второго порядка функции 
равна
…
|
|
|
|
Уравнение
наклонной асимптоты графика функции 
имеет
вид …
|
|
|
|
Частная
производная 
функции 
равна
…
|
|
|
|
Множество
первообразных функции 
имеет
вид …
|
|
|
|
Если
функция 
непрерывна
на отрезке 
и 
,
то интеграл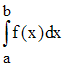 
можно
представить в виде …
|
|
|
|
Определённый
интеграл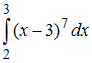 
равен
…
|
|
|
|
Площадь
фигуры, изображённой на рисунке,
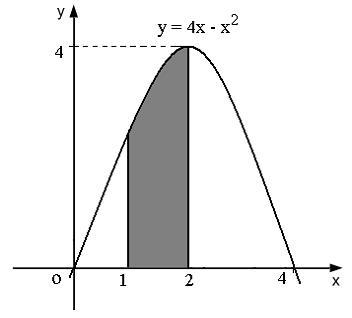равна
…
|
|
|
|
Общий
член числовой последовательности 
и 
.
Тогда 
равно
…
|
|
|
4 |
Даны
числовые ряды:
1) 
;
2) 
.
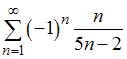Тогда
имеет место одна из следующих ситуаций:
…
|
|
|
ряд 1) сходится, ряд 2) расходится |
Если
радиус сходимости степенного
ряда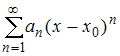 
равен R,
то интервал сходимости этого ряда имеет
вид …
|
|
|
|
Рядом
Маклорена для функции 
является
…
|
|
|
|
Уравнение 
является
…
|
|
|
линейным неоднородным дифференциальным уравнением первого порядка |
Общее
решение дифференциального уравнения
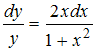имеет
вид …
|
|
|
|
Общее
решение дифференциального уравнения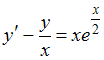 
имеет
вид …
|
|
|
|
, 
Решение
задачи Коши 
, 
имеет
вид …
|
|
|
|
Общее
решение линейного однородного
дифференциального уравнения второго
порядка 
имеет
вид …
|
|
|
|
, 
Общее
решение дифференциального уравнения 
имеет
вид …
|
|
|
|
,
Из урны, в которой находятся 7 черных и 3 белых шаров, вынимают одновременно 2 шара. Тогда вероятность того, что оба шара будут черными, равна …
|
|
|
|
Устройство состоит из двух элементов, работающих независимо. Вероятности безотказной работы этих элементов (в течение рабочего дня) равны соответственно 0,8 и 0,9. Тогда вероятность того, что в течение рабочего дня будут работать безотказно оба элемента, равна …
|
|
|
0,72 |
В первой урне 8 черных и 2 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна …
|
|
|
0,25 |
Дискретная
случайная величина 
задана
законом распределения вероятностей:
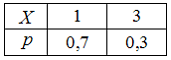Тогда
ее функция распределения вероятностей
имеет вид …
|
|
|
|
Непрерывная
случайная величина 
задана
плотностью распределения вероятностей:
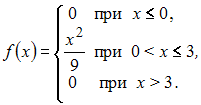Тогда
вероятность 
равна
…
|
|
|
|
Функция
распределения вероятностей равномерно
распределенной случайной величины 
изображена
на рисунке:
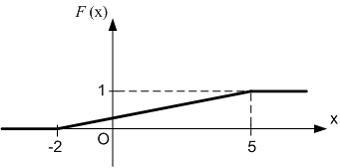Тогда
ее дисперсия равна …
|
|
|
|
|
|
|
|
Из
генеральной совокупности извлечена
выборка объема 
,
полигон частот которой имеет вид:
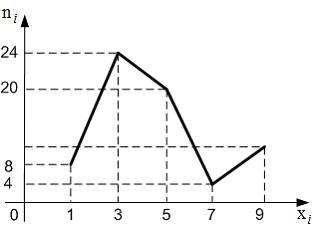Тогда
число вариант 
в
выборке равно …
|
|
|
11 |
Мода вариационного ряда 3, 4, 6, 6, 7, 10, 11, 12 равна …
|
|
|
6 |
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 4,5; 5,5; 6,5. Тогда несмещенная оценка дисперсии равна …
|
|
|
1 |
Дан
доверительный интервал 
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда точечная оценка
математического ожидания равна …
|
|
|
12,8 |
Выборочное
уравнение парной регрессии имеет вид
.
Тогда выборочный коэффициент регрессии
равен …
|
|
|
1,6 |
|
|
|
|
Левосторонняя критическая область может определяться из соотношения …
|
|
|
|
|
|
|
|
Область
допустимых решений 
задачи
линейного программирования имеет
вид:
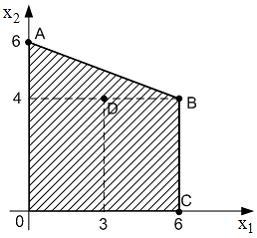Тогда
максимальное значение функции 
достигается
в точке …
|
|
|
B |
Максимальное
значение целевой функции 
при
ограничениях
равно
…
|
|
|
22 |
Транспортная
задача
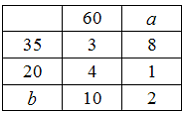будет
закрытой, если …
|
|
|
|
, 
Матричная
игра задана платежной матрицей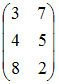 
.
Тогда верхняя цена игры равна …
|
|
|
7 |
Матрица
выигрышей в игре с природой имеет
вид:
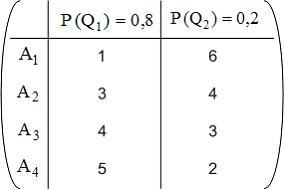Тогда
оптимальной, по критерию Байеса, будет
стратегия …
|
|
|
|
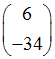
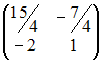
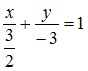
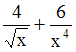
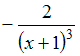
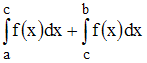
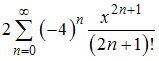
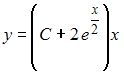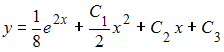