Пример задачи, решаемой методом кусочно-линейной аппроксимации

Задача. Найти минимум функции при ограничениях:

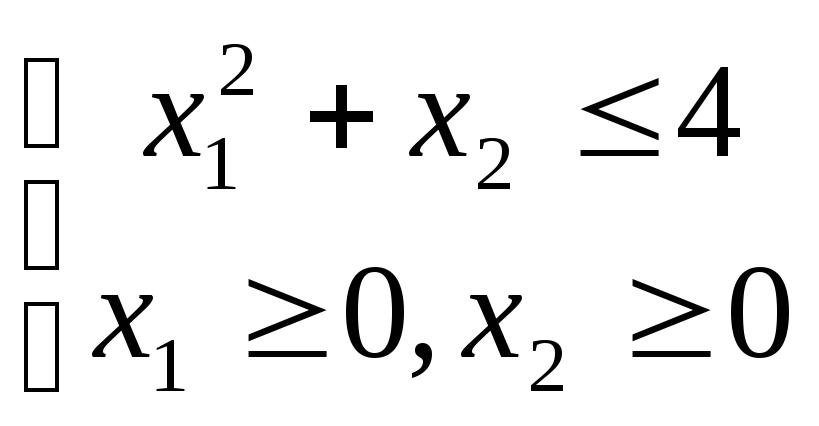
Решить данную задачу методом кусочно-линейной аппроксимации.

Решение.

Данная задача является задачей ВП. При условии неотрицательности переменных неравенство показывает, чтоможет изменяться лишь от 0 до 2, а– от 0 до 4.

Отрезок [0;2] разобьем точками , а отрезок [0;4] точкамиПоложим:.

Удобно сначала вычислить необходимые значения этих функций (т. к. имеем лишь одно ограничение, т. е. m=1, будем писать  ₁ и  ₂ вместо  ₁₁ и ₁₂).

x1	x10	x11	x12		x2	x20	x21	x22	x23	x24
x1	0	1	2		x2	0	1	2	3	4
	0	1	4			0	1	2	3	4
f1	2	0	2		f2	4	1	0	1	4

По формулам имеем:

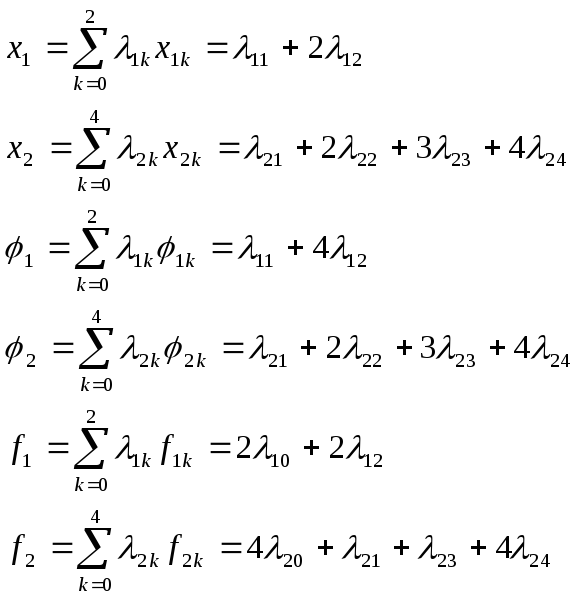
Таким образом, приближенная задача для данной задачи ВП имеет вид: найти минимум функции при ограничениях:

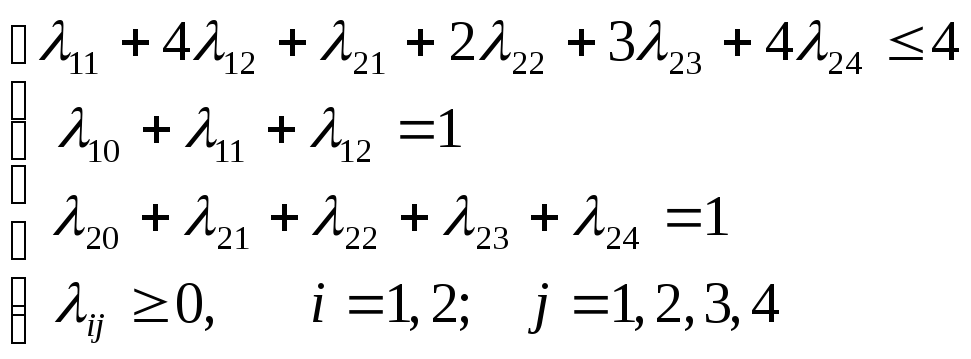
Решая данную задачу линейного программирования, как описано ранее, получим:

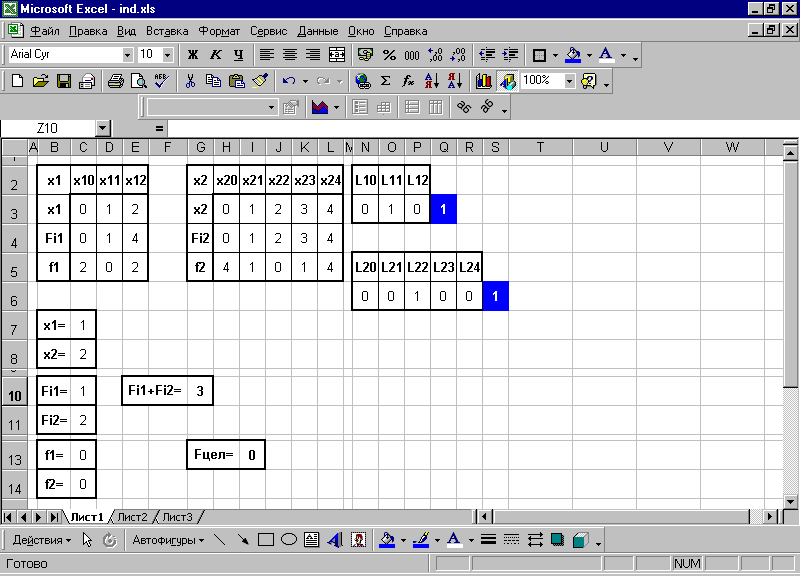
Таким образом, оптимальное решение приближенной задачи (1;2), и .

Задачи для самостоятельного решения

1. Найти максимум функции при ограничениях

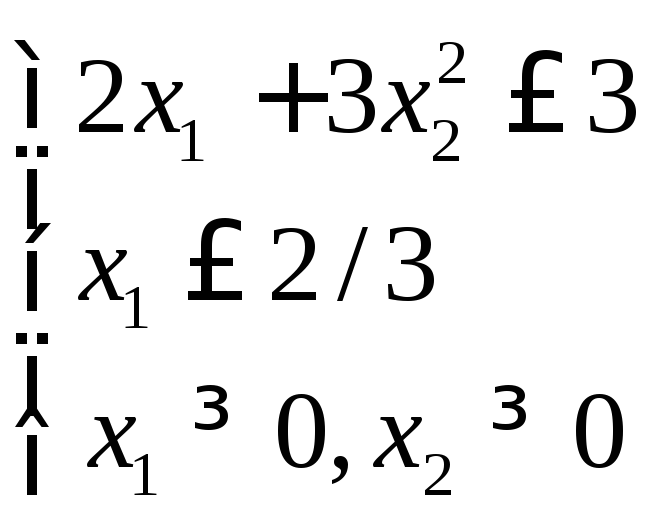
2. Найти минимум функции при ограничениях

3. Найти максимум функции при ограничениях

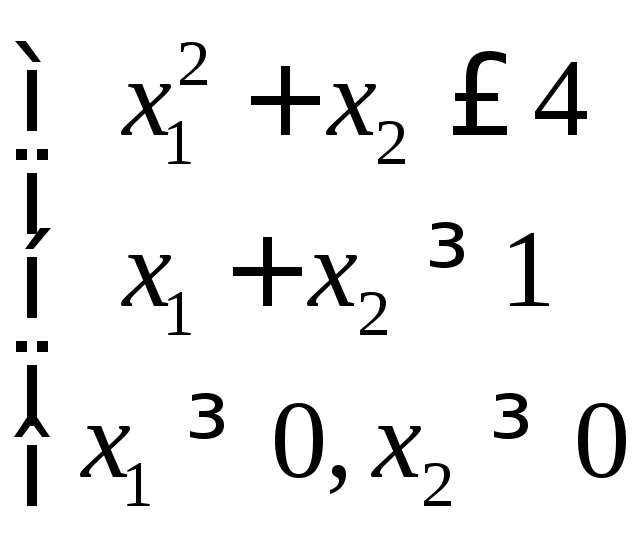
Лабораторная работа № 5. Игровые модели

Пусть антагонистическая игра двух участников задана платежной матрицей ||a_ij||, с положительными элементами (условия положительности всегда можно добиться, прибавив ко всем элементам матрицы одно и тоже положительное число) и не имеет седловую точку. Тогда ее решение может быть найдено с помощью ЗЛП. Так, для 1-го игрока достаточно найти min f=x₁+x₂+…+x_m при системе ограничений ,x_i ≥0, для , а затем вектор оптимальных смешанных стратегий (p₁ ,p₂ ,…,p_m), где . Для второго игрока необходимо найти max f= x₁+x₂+…+x_n при системе ограничений ,x_i ≥0, для а затем вектор оптимальных смешанных стратегий (p₁ ,p₂ ,…,p_n), где .

Пример задачи по теории игр, решаемой симплексным методом

Задача. Первый и второй игроки одновременно и независимо друг от друга показывают один, два или три пальца. Выигрыш или проигрыш (в денежных единицах) равен общему количеству показанных пальцев. Если это количество четное, то выигрывает первый игрок, а второй ему платит. Если же оно нечетное, то выигрывает второй игрок, а первый ему платит. Найти оптимальные стратегии каждого игрока.

Экономико-математическая модель

У каждого игрока имеется по три стратегии: показать один, два или три пальца. В соответствии с этим платежная матрица будет выглядеть следующим образом:

Выберем минимальные значения в каждой строке, а затем из них найдем максимальное. Это даст нам нижнюю цену игры. Она равна -3. Выберем максимальные значения в каждом столбце, а затем из них найдем минимальное. Получим верхнюю цену игры. Она равна 4. Так как нижняя цена игры не совпадает с верхней, то решение будем искать в смешанных стратегиях. Прибавляя ко всем элементам матрицы число, равное 5, перейдем к матрицы модифицированной игры:

,

которой соответствует задача линейного программирования для 1 игрока:

min f(x₁, x₂, x₃) =x₁+x₂+x₃

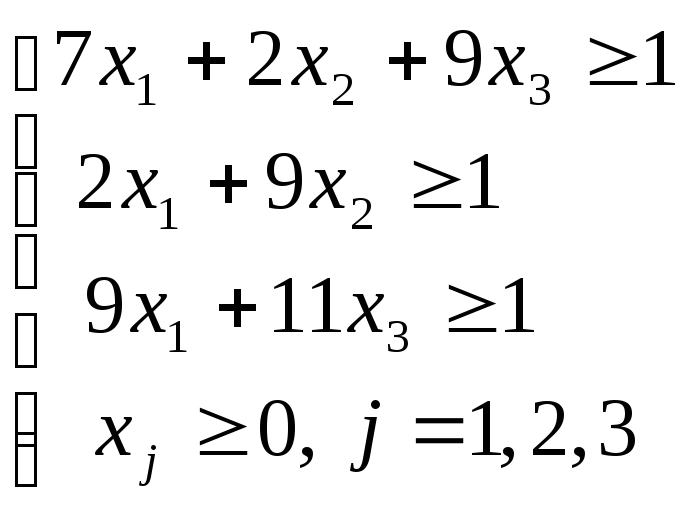
и задача линейного программирования для 2 игрока:

max f(x₁, x₂, x₃) =x₁+x₂+x₃

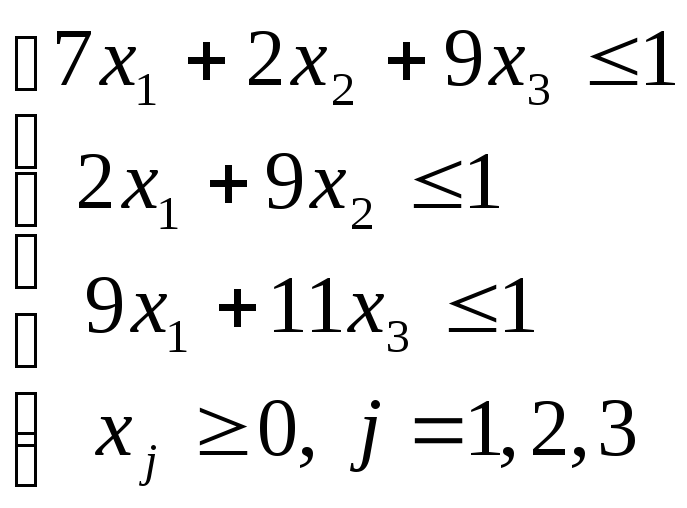
Решение.

Воспользовавшись симплексным методом, получим решения обеих задач, как описано ранее. Результаты приведены на рисунке.

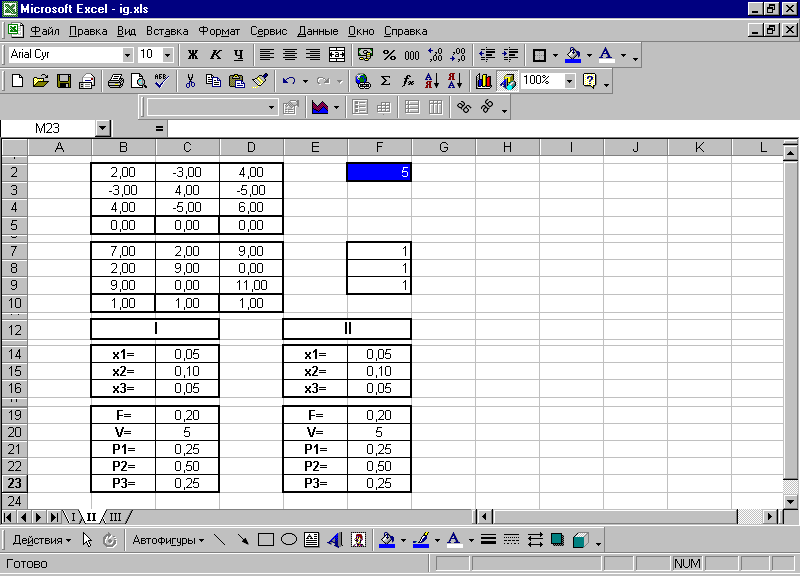
Таким образом, оптимальная смешанная стратегия 1-го игрока совпадает с оптимальной смешанной стратегией 2-го игрока и равна (0,25;0,5;0,25).