
- •И. В. Добрынина, р. Р. Яфаева
- •Введение
- •Лабораторная работа № 1. Задачи линейного и целочисленного линейного программирования Технология компьютерной реализации
- •Задача линейного программирования
- •Пример задачи линейного программирования
- •Задача целочисленного линейного программирования
- •Пример задачи целочисленного линейного программирования
- •Задачи для самостоятельного решения
- •Лабораторная работа № 2. Задачи транспортного типа
- •Примеры задач транспортного типа
- •Задачи для самостоятельного решения
- •Лабораторная работа № 3. Модели нелинейной оптимизации
- •Технология компьютерной реализации
- •Пример задачи нелинейной оптимизации
- •Задачи для самостоятельного решения
- •Лабораторная работа №4. Метод кусочно-линейной аппроксимации
- •Пример задачи, решаемой методом кусочно-линейной аппроксимации
- •Задачи для самостоятельного решения
- •Лабораторная работа № 5. Игровые модели
- •Пример задачи по теории игр, решаемой симплексным методом
- •Задачи для самостоятельного решения
- •Лабораторная работа № 6. Динамическое программирование
- •Задачи для самостоятельного решения
- •Литература
Пример задачи нелинейной оптимизации
Задача. Необходимо сформировать оптимальный портфель Марковица (минимального риска) трех ценных бумаг с эффективностями и рисками: (4,10), (10,40), (40,80). Нижняя граница доходности портфеля задана равной 15.
Экономико-математическая модель
Пусть xj, j= 1,2,3 – доля капитала, потраченная на покупку ценных бумагу j-го вида (весь выделенный капитал принимается за 1)
![]()
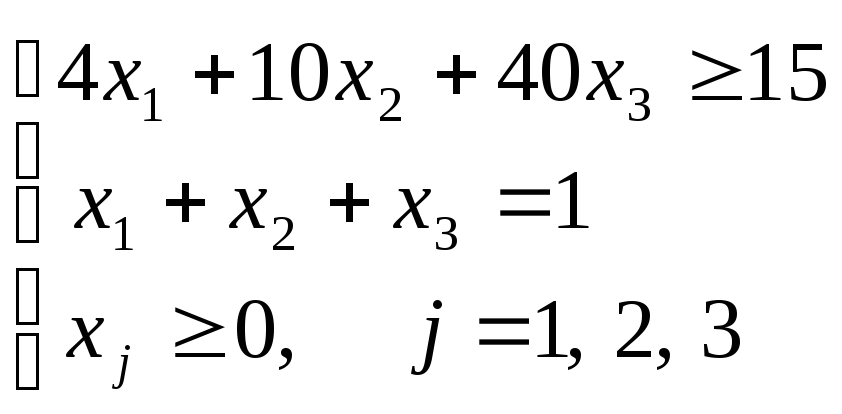
Решение.
Приведенная ЭММ является моделью задачи нелинейного программирования. Специальный (рабочий) лист может быть подготовлен в виде:
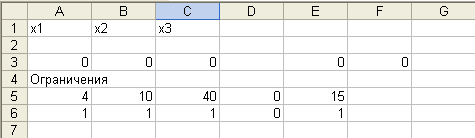
формулы этого листа приведены в ячейках.

Диалоговое окно Поиск решения с введенными ограничениями, соответствующее приведенному выше рабочему листу:
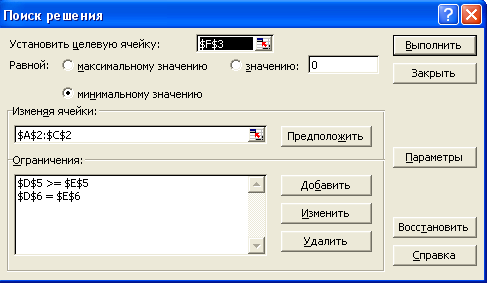
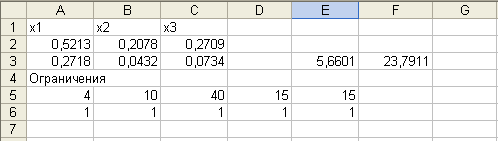
Реализуя приведенную модель средствами MS Excel, будем иметь оптимальный портфель Марковица:
х1 = 0,5213, х2 = 0,2078, х3 = 0,2709,
т.е. доли ценных бумаг оказались равными 52,13%; 20,78% и 27,09%. При этом минимальный риск – 23,79, доходность портфеля оказалась равной заданной – 15.
Задачи для самостоятельного решения
1. Предприятие располагает двумя способами производства данного вида продукции. В течение рассматриваемого периода времени необходимый объем продукции равен 100= Х1 + Х2, где Х1 и Х2 – объемы производства по соответствующему технологическому способу. Затраты производства S при каждом способе зависят от объемов нелинейно:
![]() ,
,
![]() .
.
Необходимо так распределить объем производства между технологическими способами, чтобы минимизировать общие затраты производства.
2. Найти
максимальное значение функции
![]() при ограничениях:
при ограничениях:
![]()
3. Необходимо сформировать оптимальный портфель Марковица (минимального риска) трех ценных бумаг с эффективностями и рисками: (6,10), (10,50), (60,80). Нижняя граница доходности портфеля задана равной 20.
4. Найти
минимум функции
![]() при ограничениях:
при ограничениях:
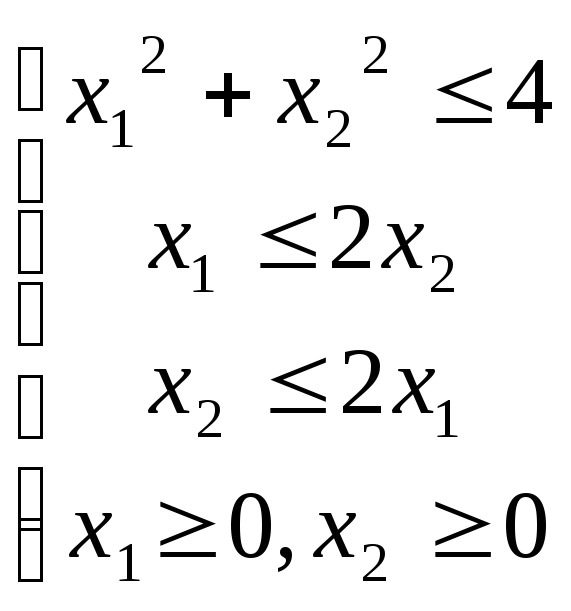
Лабораторная работа №4. Метод кусочно-линейной аппроксимации
Пусть дана система
неравенств вида
![]()
![]() и целевая функция
и целевая функция![]() ,
причем все функции
,
причем все функции![]() являются выпуклыми, а функцияz
выпукла или вогнута на некотором
выпуклом множестве М.
являются выпуклыми, а функцияz
выпукла или вогнута на некотором
выпуклом множестве М.
Рассмотрим приближенное решение задач выпуклого программирования с сепарабельными функциями методом кусочно-линейной аппроксимации.
Функция F(X)=F(![]() ,…,xn)
называется сепарабельной, если ее можно
представить в виде суммы функций, каждая
из которых зависит только от одной
переменной, т. е. если
,…,xn)
называется сепарабельной, если ее можно
представить в виде суммы функций, каждая
из которых зависит только от одной
переменной, т. е. если
![]() или
или
![]()
(не исключено, что
![]() при некоторыхi).
при некоторыхi).
Пусть в задаче ВП
и функция цели z,
и все ограничения
![]() являются сепарабельными. Тогда задача
имеет вид: найти минимум выпуклой
(максимум вогнутой) функции
являются сепарабельными. Тогда задача
имеет вид: найти минимум выпуклой
(максимум вогнутой) функции![]() при ограничениях:
при ограничениях:
![]()
![]() .
.
Идея метода
кусочно-линейной аппроксимации состоит
в том, что все
![]() и все
и все![]() заменяются
ломаными линиями, состоящими из
прямолинейных отрезков. При этом исходная
задача ВП заменяется новой, приближенной
задачей, которая является задачей
линейного программирования. Эта задача
решается обычно симплексным методом,
и ее решение является приближенным
решением исходной задачи ВП.
заменяются
ломаными линиями, состоящими из
прямолинейных отрезков. При этом исходная
задача ВП заменяется новой, приближенной
задачей, которая является задачей
линейного программирования. Эта задача
решается обычно симплексным методом,
и ее решение является приближенным
решением исходной задачи ВП.
Для построения
приближенной задачи рассмотрим
кусочно-линейную аппроксимацию функции
одной переменной h(x),
заданной на отрезке [0,a].
Разобьем этот отрезок на r
частей точками x![]() <x
<x![]() <…<x
<…<x![]() так, чтобы x
так, чтобы x![]() =0,
x
=0,
x![]() =a.
Вычислим значения функции h
=a.
Вычислим значения функции h![]() (x)
(k=0,…,r)
в этих точках. Соединим попарно точки
(x
(x)
(k=0,…,r)
в этих точках. Соединим попарно точки
(x![]() ;h
;h![]() )
и (x
)
и (x![]() ;h
;h![]() )
отрезками прямых. Состоящая из этих
отрезков ломаная
)
отрезками прямых. Состоящая из этих
отрезков ломаная![]() аппроксимирует функциюh(x)
на отрезке[0,a].
аппроксимирует функциюh(x)
на отрезке[0,a].
Уравнение
участка ломаной
![]() между
точками (x
между
точками (x![]() ;h
;h![]() )и
(x
)и
(x![]() ;h
;h![]() )
имеет вид
)
имеет вид![]() (уравнение прямой, построенной по двум
заданным точкам).
(уравнение прямой, построенной по двум
заданным точкам).
Если каждое из
отношений в этом равенстве обозначить
через
![]() ,
то получим:
,
то получим:
![]() и
и
![]() ,
причем
,
причем![]() .
.
Обозначив
![]() ,
можно переписать в виде:
,
можно переписать в виде:
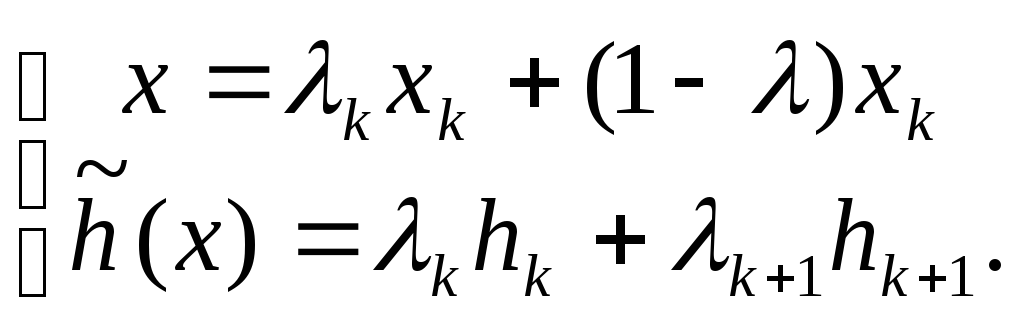
Таким образом, для любого x[0,a] уравнение ломаной можно записать в виде:
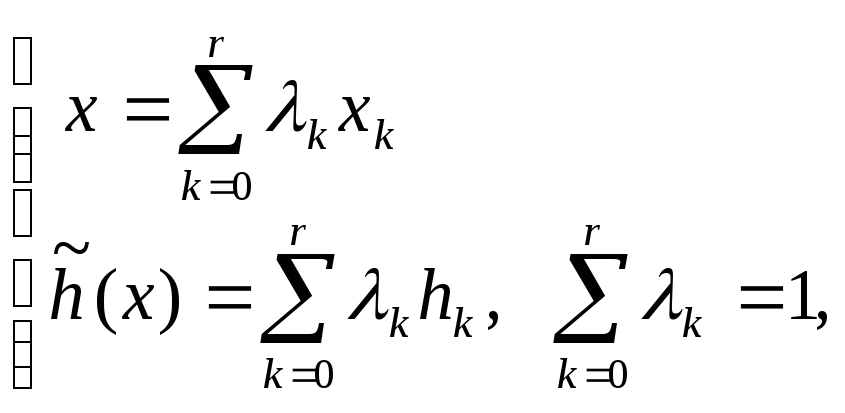 ,
,
причем всегда отличны от нуля только для значения k (если x является внутренней точкой k-го отрезка разбиения), или одно, (если x совпадает с концом отрезка).
Возвращаясь к
задаче ВП с сепарабельными функциями,
отметим, что, прежде всего (в зависимости
от системы ограничений) нужно определить
интервал изменения каждой переменной
x![]() .
Затем каждый этот интервал разбивается
на части точкамиx
.
Затем каждый этот интервал разбивается
на части точкамиx![]() и, с использованием полученных формул
строится кусочно-линейная аппроксимация
для функцийf
и, с использованием полученных формул
строится кусочно-линейная аппроксимация
для функцийf![]() и
и![]() .
После этого можно для исходной задачи
записать приближенную задачу: найти
максимум функции
.
После этого можно для исходной задачи
записать приближенную задачу: найти
максимум функции![]() при ограничениях:
при ограничениях:
![]()
![]()
![]()
