5. Теорема сложения вероятностей. Следствие.

События А и В назыв. совместными, если они могут произойти оба в результате одного опыта. В противном события называются несовместными.

Противоположными называются два единственно возможных события, образующих полную группу. Если одно из событий, являющихся противоположными, обозначить через А, то противоположное событие обозначают через .

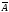Р(А+В)=Р(А)+Р(В)-Р(АВ), (вероятность суммы 2х соб = сумме вероятностей 2х соб – вероятность их совместного произведения)

Следствия:

1.Для несовместимых соб: Р(А+В)=Р(А)+Р(В), т.к. Р(АВ)=0

2.Для противоположных соб. Р(А+неА)=Р(А)+Р(неА)-Р(А*неА)=1- Р(А*неА) Р(А)+Р(неА)=1,т.к. противолож соб, образуют полную группу событий.

6. Условная вероятность. Зависимые соб и независиме сб. Схема урн.

Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А.

Условной вероятностью Р(В|А), называют вер соб В, вычисленную в предположении, что соб А уже наступило.

Следствия:

1.Р(АВ)=Р(В|А)Р(А)

2.Если Р(А)=0, то изложенное определение условной вероятности неприменимо.

Соб А и В независимые, если Р(В|А)=Р(А). Соб А и В зависимые, если Р(В|А)≠Р(А).

СХЕМА УРН, ИЗВЛЕЧЕНИЯ БЕЗ ВОЗВРАЩ: В урне 2Б и 3Ч шара. Два игрока вынимают из урны поочередно шары, не возвращая их обратно. Выиграет тот, кто раньше извлечет белый шар. Найти вероятность того, что выиграет начинающий.

Введём обозначения событий

A = {выиграл первый игрок};

B = {выиграл второй игрок}

Составим из извлечённых шаров упорядоченное множество. Белый шар может впервые встретиться в составленном нами множестве под номером от 1 до 4. Действительно, в крайнем случае все 3 чёрных шара займут первые места. Первый игрок выигрывает в случае, если впервые белый шар встретится под номерами 1 или 3, второй игрок – при извлечении первого белого шара под номерами 2 или 4.

Задачу можно решить с применением комбинаторной формулы размещений 1.Вер извлечь белый шар первым P(1) = 2/5.

2.Вер извлечь белый шар вторым (при условии, что первым извлечён чёрный шар)   P(2) = (2/4)*(3/5) = 3/10.

3.Третьим белый шар будет извлечён (при условии извлечения первыми двух чёрных шаров) с вер P(3) = (3/5)*(2/4)*(2/3) = 1/5.

4.И наконец, четвёртым впервые будет извлечён белый шар при условии извлечения первыми тремя чёрных шаров. Вер того соб: P(4) = (3/5)*(2/4)*(1/3)= 1/10.

Вычислим искомые вероятности: P(A) = P(1) + P(3) = 2/5 + 1/5 = 3/5;

P(B) = P(2) + P(4) = 3/10 + 1/10 = 4/10 = 2/5