20. Гидродинамика вязкой жидкости, коэффициент вязкости. Течение по трубе. Формула Пуазейля. Закон подобия. Формула Стокса. Турбулентность.Движение вязких жидкостей и газов

Рейнольдс установил, что характер течения определяется значением безразмерной величины.

Где ρ — плотность жидкости и газа;

Υ — скорость потока;

ŋ— вязкость жидкости;

l — размер;

R_e —число Рейнольдса;

R_e=1320— переход от ++ движения к турбулентному

—если в качестве размера взять радиус;

В число Рейнольдоса входит отношение пластичности ρ и вязкостью η

—кинематическая вязкость , тогда число Рейнольдоса

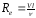
Формула Пуазейля

Скорость по оси трубки (*)

Через кольцо радиуса r пройдёт в единицу времени объём жидкости не равен произведению площади кольца 2πrdr на скорость υ(r) на расстояние r от оси:

Проинтегрируем:

Подставляем (*) в (*^/) получаем формулу Пуазейля

Поток сильно зависит от радиуса трубы. Q пропорциональна отношению т.е. перепаду давления на единицу длины трубы, а также обратно пропорциональна вязкости жидкости ŋ

Формула Стокса

Стокс установил, что при небольших скоростях и размерах тел модуль силы сопротивления определяется формулой:

ŋ— динамическая вязкость;

υ— скорость движения тела;

l— характеристический размер тела;

k— коэффициент пропорциональности, который зависит от формы тела;

Сила сопротивления в жидкостях небольших шариков при малых скоростях:

Формула Стокса справедлива при условии, что расстояние от тела до границ жидкости много больше размеров тела.

21. Основное уравнение молекулярно - кинетической теории идеального газа. Средняя кинетическая энергия поступательного движения молекулы.

МКТ—раздел физики, изучающий свойства объектов на основе их молекулярного строения.Молекула— мельчайшая частица вещества, определяющая его химические свойстваАтомы—основная часть молекулы, их набор(не деление) ограничен. <Eпост>=3/2kT

Основные положения МКТ а) вещество состоит из молекул. Доказательство: делимость тел, растворимость веществ, молекулы определяются электронным микроскопом. б) молекулы находятся в непрерывном хаотическом тепловом движении. Доказательство: давление газов,брауновское движение(хаотическое движение частиц в жидкости),диффузия(проникновение молекул одного вещества между молекулами другого вещества). в) молекулы взаимодействуют друг с другом. Доказательство: существование трёх агрегатных состояний вещества(газ. Жидкость, твёрдое тело), фазовые переходы между этими состояниями; упругие свойства твёрдых тел; поверхностное натяжений жидкостей;

Вывод основного уравнения МКТ

Давление газа на стенки сосуда определяется за счёт ударов молекул.

Предположим, что все молекулы имеют одинаковую массу m₀и движутся с одинаковой по модулю скоростью υ. Все удары молекул абсолютно упругие (предположим) Рассмотрим стенку

1 молекула передаёт стенке импульс: ∆p=m₀V_x-m₀(-V_x)=2m₀V_x

За Δtо стенку ударяетN₁молекул, тогда импульс за Δt

∆p_общ.=N₁∆p₁=2m₀V_xN₁

Давление

Концентрация n[м^-3];—полное число молекул ,число ударов, т.к. половина молекул летит к стенке, а вторая половина от стенку;;;, ∆l— расстояние от стены, которое успевают преодолеть молекулы за ∆t, чтобы удариться об неё∆l=V_x ∆t;;;;Т.к. пространство имеет три измерения, то введём среднеквадратичную скорость. Средняя скоростьИз этого следует все направления движения молекул равновероятны Среднеквадратичная скорость:

Т.к. направления равновероятны, то средние значения равны:

Следовательно: —основное уравнение МКТ газа

Средне кинетическая энергия поступательного движения молекул.