
- •Министерство образования республики беларусь
- •Оглавление
- •Введение
- •Лабораторная работа 1 Работа в среде Turbo Pascal. Программирование линейных и разветвляющихся алгоритмов Цели:
- •Процедуры ввода/вывода языка Turbo Pascal
- •Оператор присваивания
- •Задание 2.
- •Примеры решений задач
- •Задания Задание 1.
- •Задание 2.
- •Задание 3.
- •Примеры решений задач
- •Задания
- •Требования к отчету
- •Основные команды ms dos.
- •Задания Задание 1.
- •Задание 2.
- •Задание 3.
- •Требования к отчету
- •Контрольные вопросы
- •Лабораторная работа 5
- •Задание 2.
- •Задание 3.
- •Задание 4.
- •Требования к отчету
- •Контрольные вопросы
- •Лабораторная работа 6 Архиваторы. Антивирусные программы Цели:
- •Общие положения
- •Задания Задание 1.
- •Задание 2.
- •Задание 3.
- •Требования к отчету
- •Контрольные вопросы
- •Лаборторная работа 7 Текстовый процессор Microsoft Word Цели:
- •Общие положения
- •Задания Задание 1.
- •Задание 2.
- •Задание 3.
- •Задание 4.
- •Задание 5.
- •Задание 6.
- •Задание 7.
- •Задание 8.
- •Требования к отчету
- •Контрольные вопросы
- •Лабораторная работа 8 Табличный процессор Microsoft Excel Цели:
- •Общие положения
- •Задания
- •Задание 1.
- •Задание 3.
- •Задание 4.
- •Задание 5.
- •Метод Крамера
- •Матричный способ решения
- •Решение слау методом Гаусса
- •Требования к отчету
- •Контрольные вопросы
- •Лабораторная работа 9 Система управления базами данных Microsoft Access Цели:
- •Общие положения
- •Задания Задание 1.
- •Задание 2.
- •Задание 3.
- •Задание 4.
- •Задание 5.
- •Требования к отчету
- •Контрольные вопросы
- •Лабораторная работа 10 Графический редактор Corel Draw Цели:
- •Общие положения
- •Задания Задание 1.
- •Задание 2.
- •Задание 3.
- •Задание 3.
- •Требования к отчету
- •Контрольные вопросы
- •Список использованных источников
- •Информатика
Матричный способ решения
Матричный
способ решения СЛАУ достаточно прост.
Обе части матричного равенства
![]() умножим слева на обратную матрицу
умножим слева на обратную матрицу![]() .
Тогда решение системы запишется в
следующем виде
.
Тогда решение системы запишется в
следующем виде
![]() .
.
Записываем СЛАУ на текущий лист аналогично предыдущему примеру (Рис. 8.7).

Рисунок 8.7 — Вид записи матрицы на рабочем листе
Для
решения системы необходимо найти для
матрицы
![]() обратную
обратную![]() и умножить ее справа на вектор-столбецB свободных
членов. Для чего, воспользовавшись
функциями Excel МУМНОЖ(матрица1; матрица2)
и МОБР(матрица), введем в интервал B7:B9
табличную, т. е. используем для ввода
комбинацию клавиш CTRL+SHIFT+
ENTER, мегаформулу
МУМНОЖ(МОБР(A3:C5);D3:D5).
и умножить ее справа на вектор-столбецB свободных
членов. Для чего, воспользовавшись
функциями Excel МУМНОЖ(матрица1; матрица2)
и МОБР(матрица), введем в интервал B7:B9
табличную, т. е. используем для ввода
комбинацию клавиш CTRL+SHIFT+
ENTER, мегаформулу
МУМНОЖ(МОБР(A3:C5);D3:D5).
После чего в строке формул увидим {=МУМНОЖ(МОБР (A3:C5);D3:D5)}, а в интервале B7:B9 — решение, точно такое же, как и в предыдущем случае (см. рис. 8.6).
Решение слау методом Гаусса
Найдем решение системы:
 .
.
В ячейки А1:Е4 вводим расширенную матрицу системы.
Эту матрицу копируем в диапазоны ячеек А6:Е9
Прямой ход метода Гаусса. Предположим, что в ячейке А1 не ноль. Если это не так, то переставим строки таким образом, чтобы число в ячейке А1 было отлично от нуля.
Выделяем диапазон А7:Е7 и в строке формул вводим формулу:
=A2:E2-$A$1:$E$1*A2/$A$1
и нажимаем CTRL+SHIFT+ENTER. При этом формула примет вид:
{=A2:E2-$A$1:$E$1*A2/$A$1},
где фигурные скобки указывают на операции над матрицами.
Протащив за маркер
автозаполнения, скопируем формулу в
ячейки А8:Е9. В результате этих операций
коэффициенты при
![]() во всех уравнениях кроме первого
обратятся в ноль.
во всех уравнениях кроме первого
обратятся в ноль.
Выделяем диапазон А6:Е9 и копируем значения, хранящиеся в нём в ячейки диапазонов А11:Е14. Для копирования значений нужно воспользоваться специальной вставкой. Ей соответствует пункт меню Правка->Специальная вставка, после выбора которого появляется диалоговое окно Специальная вставка, в котором нужно выбрать Вставить->Значения и нажать кнопку Ок.
Аналогичным образом
обращаем в ноль коэффициенты при
![]() .
В диапазон ячеек В13:Е13 вводим формулу
.
В диапазон ячеек В13:Е13 вводим формулу
=B8:E8-$B$7:$E$7*B8/$B$7
Протащим маркер
автозаполнения этого диапазона так,
чтобы заполнить ячейки диапазона
В14:Е14. Это обратит в ноль коэффициенты
при
![]() в двух последних уравнениях.
в двух последних уравнениях.
Далее содержимое (только значения!) диапазона A11:Е14 скопируем в ячейки диапазона A16:Е19.
Выделим диапазон С19:Е19 введем в него формулу
{=C14:E14-$C$13:$E$13*C14/$C$13},
что обратит в ноль коэффициент при х3 в последнем уравнении.
В результате этих преобразований матрица системы примет треугольный вид:
B$7:$E$7*B8/$B$7.
Протащим маркер автозаполнения этого диапазона так, чтобы заполнить ячейки диапазона В14:Е14. Это обратит в ноль коэффициенты при х2 в последних двух уравнениях.
Далее содержимое (только значения!) диапазона A11:Е14 скопируем в ячейки диапазона A16:Е19.
Выделим диапазон С19:Е19 введем в него формулу
{=C14:E14-$C$13:$E$13*C14/$C$13},
что обратит в ноль коэффициент при х3 в последнем уравнении.
В результате этих преобразований матрица системы примет треугольный вид (рис. 8.8).
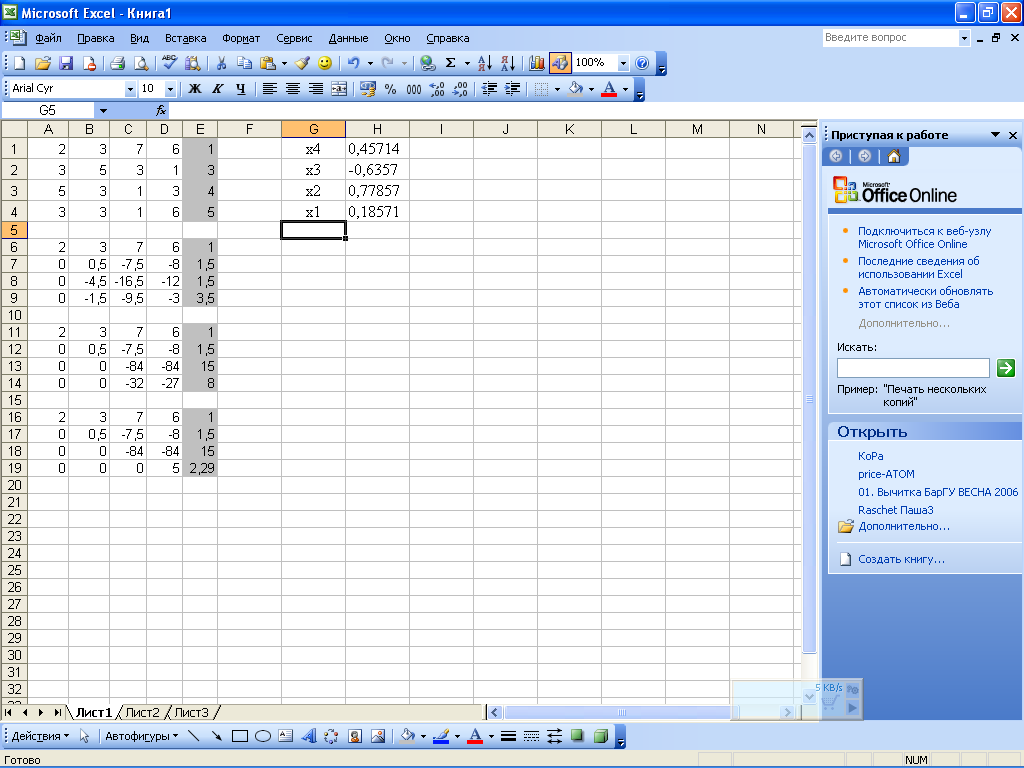
Рисунок 8.8 — Вид записи матрицы на рабочем листе
Обратный ход метода Гаусса. В ячейки G1, G2, G3 и G4 введем «х4», «x3», «x2» и «х1» соответственно, а в ячейки Н1:Н4 — представленные ниже формулы:
|
Ячейка |
Формула |
|
Н1 |
=E19/D19 |
|
Н2 |
=(E18-D18*H1)/C18 |
|
Н3 |
=(E17-D17*H1-C17*H2)/B17 |
|
Н4 |
=(E16-D16*H1-C16*H2-B16*H3)/A16 |
В результате чего в диапазоне Н1:Н4 будет получено решение системы.
