2 курс ФК, ЕП, УП Денне / Волошина Статистика Курс лекцій 2011 / Статистика Волошина Електр посібнКурс лекцій із дисц статистика 2011 / 10 / schilnist swjasku

Вимірювання щільності зв'язку

Дисперсія, на відміну від інших характеристик варіації, є адитивною величиною. Тобто, у структурованій сукупності, яка поділена на групи за факторною ознакою Х, дисперсія результативної ознаки Y може бути розкладена на: дисперсію у кожній групі (внутрішньогрупову дисперсію) та дисперсію між групами (міжгрупову). Загальна дисперсія характеризує варіацію ознаки Y за рахунок впливу всіх причин (факторів) міжгрупова – за рахунок впливу фактора Х, покладеного в основу групування внутрішньогрупові – за рахунок усіх інших факторів, крім фактора Х.

Центром розподілу сукупності в цілому є загальна середня, яка обчислюється за формулою:

,

де у_і – індивідуальні значення окремої ознаки

f_i – частота окремої ознаки.

Центром розподілу в окремій j-й групі є групова середня, яка обчислюється за формулою:

,

де у_іj – індивідуальне значення окремої ознаки, яка потрапила до j-ї групи

f_{i j} – частота окремої ознаки, яка потрапила до j-ї групи.

Загальна дисперсія відображає варіацію ознаки у навколо загальної середньої та розраховується за формулою:

.

Групова дисперсія відображає варіацію відносно групової середньої та розраховується за формулою:

.

Оскільки в групи об’єднуються певною мірою схожі елементи сукупності, то варіація в групах, як правило, менша, ніж у цілому по сукупності. Якщо причинні комплекси, що формують варіацію в різних групах, неоднакові, то й групові дисперсії відрізнятимуться між собою. Узагальнюючою мірою внутрішньогрупової варіації є середня з групових дисперсій, яка обчислюється за формулою:

,

де  ²_j – групова дисперсія j-ї групи

f_j – обсяг j–ї групи.

Групові середні під впливом різних причинних комплексів також виявляються різними. Мірою варіації групових середніх навколо загальної середньої є міжгрупова дисперсія, яка обчислюється за формулою:

.

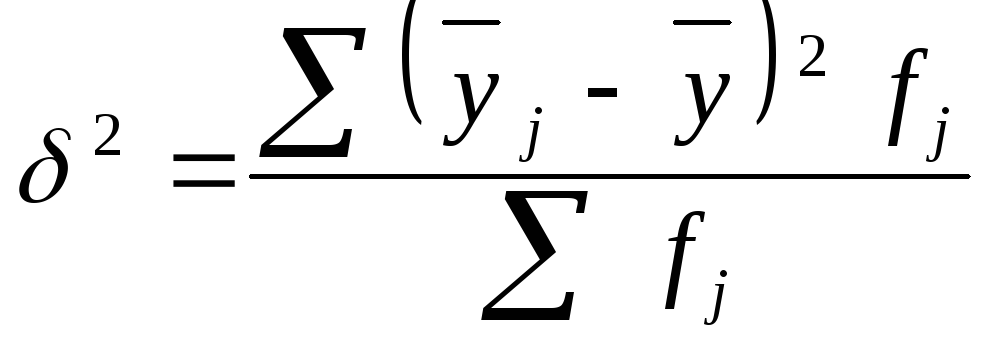Таким чином, загальна дисперсія складається з двох частин, одна з яких характеризує внутрішньогрупову варіацію, а інша – міжгрупову. Взаємозв’язок між трьома дисперсіями дістав назву правила складання дисперсій, у деяких джерелах це правило називається правилом розкладання варіації. Розглянуті три дисперсії пов’язані таким рівнянням:

На цьому взаємозв'язку базується визначення коефіцієнта детермінації (або кореляційне відношення), який характеризує, наскільки варіація результативної ознаки залежить від ознаки, яка покладена в основу групування:

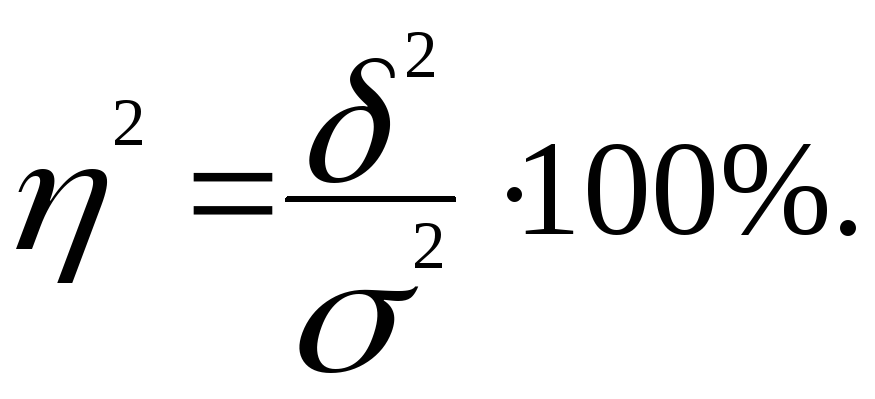
Наприклад, якщо у розподілі робітників фірми за рівнем освіти, результативною ознакою є місячна заробітна плата робітника, а визначений за результатами аналітичного групування і розрахунку міжгрупової та загальної дисперсій коефіцієнт детермінації дорівнює 48%, то це свідчить про те, що рівень заробітної плати робітника даної фірми на 48% залежить від рівня освіти, а на 100-48=52% - від всіх інших чинників, які не враховані у даному групуванні.

Емпіричне кореляційне відношення - це корінь квадратний з коефіцієнта детермінації. За абсолютним розміром він може змінюватись від 0 до 1. Якщо ή = 0, ознака групування не справляє впливу на результативну ознаку. Якщо ή = 1, зміна результативної ознаки цілком зумовлена ознакою групування, тобто між ними є функціональний зв'язок. Характеристика щільності зв’язку за рівнем емпіричного кореляційного відношення наведена у табл. 10.1.

Якщо результативна ознака у зовсім не зв'язана з х_і , то групові середні не будуть змінюватися зі зміною x_і, тобто дорівнюватимуть одна одній і дорівнюватимуть загальній середній , а міжгрупова дисперсія буде дорівнювати нулю.

Таблиця 10.1

Залежність між числовим емпіричним кореляційним відношенням та оцінкою щільності зв’язку

Емпіричне кореляційне відношення	Оцінка щільності зв’язку
0 – 0,1 0,1 – 0,3 0,3 – 0,5 0,5 – 0,7 0,7 – 0,9 0,9 – 0,999	Відсутній Слабкий Помірний Відчутний (помітний) Щільний (високий) Дуже щільний (надто високий)

Якщо результативна ознака у функціонально зв'язана з ознакою-фактором x_i, то в кожній групі внутрішньогрупова дисперсія буде дорівнювати нулю, оскільки ознака х_і у середині групи не варіює. Середня з групових дисперсій буде дорівнювати нулю, також згідно з правилом складання дисперсій =