Решение ТМО

Примеры решения типовых задач

Задача (1-10). Среднее число вызовов, поступающих на станцию скорой помощи за один час, равно . Поток вызовов простейший. Найти:

а) математическое ожидание, дисперсию, среднее квадратическое отклонение непрерывной случайной величины T – интервала времени между двумя последовательными вызовами в потоке;

б) вероятность того, что за t минут поступит: m вызовов; менее m вызовов; не менее m вызовов.

= 50 час^–1, t = 6 мин = 0,1 час^–1, m = 3.

Решение.

а) непрерывная случайная величина T – интервал времени между двумя последовательными вызовами в простейшем потоке – имеет показательный закон распределения с параметром .

Из теории вероятностей известно, что для непрерывной случайной величины , имеющей показательный закон распределения с параметром , математическое ожидание равно , дисперсия равна , среднее квадратическое отклонение равно

Следовательно, у непрерывной случайной величины T:

математическое ожидание ,

дисперсия ,

среднее квадратическое отклонение .

б) Вероятность появления событий в простейшем потоке, интенсивность которого , за время определяется формулой Пуассона .

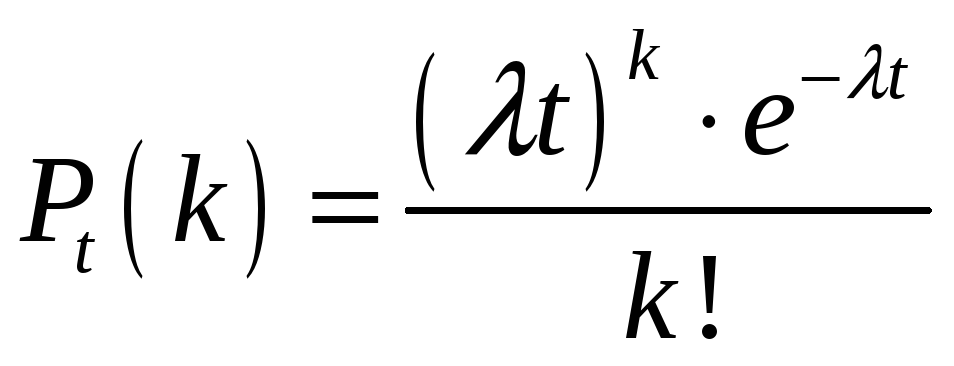Тогда вероятность того, что за 6 минут (0,1 час) поступит 3 вызова, равна

;

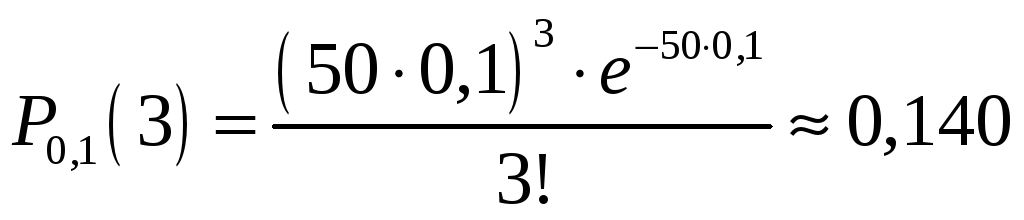вероятность того, что за 6 минут (0,1 час) поступит менее 3 вызовов, равна

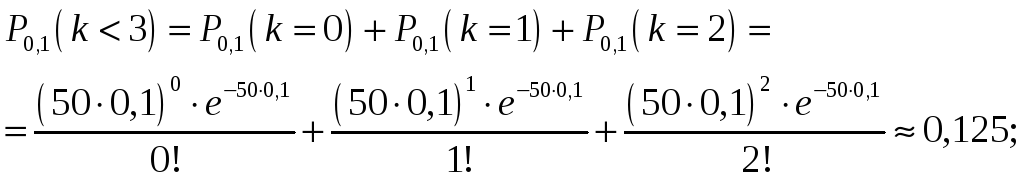
вероятность того, что за 6 минут (0,1 час) поступит не менее 3 вызовов, равна

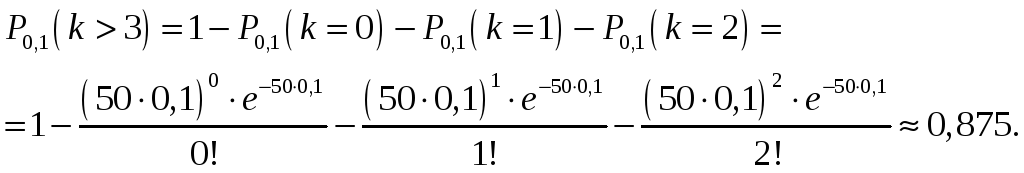
Ответ.

а) , , ;

б) ,

Задача (11-20). Электронное устройство работает в ждущем режиме и переключается очередным импульсом. Поток импульсов является потоком Эрланга k – го порядка с интенсивностью импульсов в час. В случайный момент времени устройство включается в сеть и ждет первого очередного импульса. Найти плотность распределения вероятностей времени ожидания очередного импульса и построить ее график. Вычислить вероятность того, что устройство останется в ждущем режиме не более t минут. Ответ дать с тремя десятичными знаками.

Указание: плотность распределения времени ожидания первого очередного события для потока Эрланга k – го порядка имеет вид

,

где – интенсивность простейшего потока, из которого получен поток Эрланга k – го порядка.

k = 3, = 1 час^-1, t = 12мин = 0,2 час^-1.

Решение.

Плотность распределения вероятностей времени ожидания очередного импульса для потока Эрланга 3-порядка имеет вид

,

,

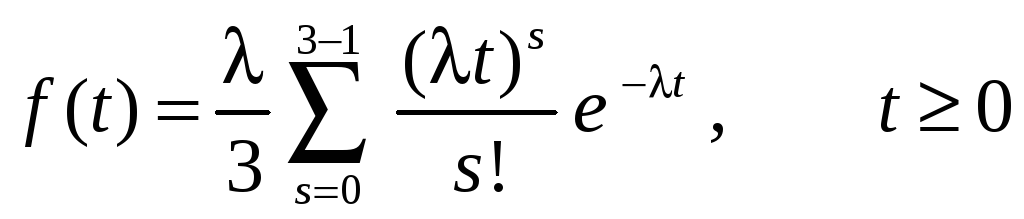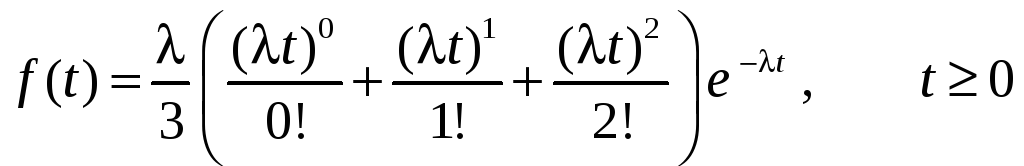По условию , тогда ,

Следовательно,

, и .

Таким образом,

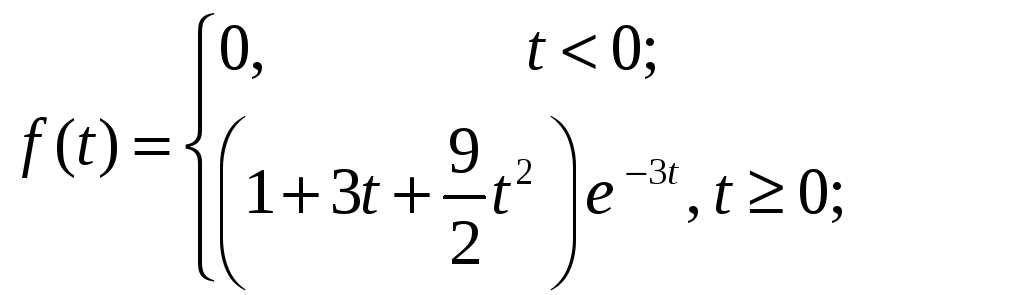
Построим график функции в пакете MathCAD:

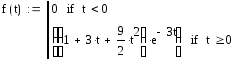
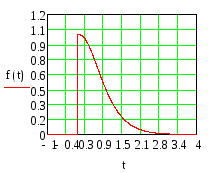
Вычислим вероятность того, что устройство останется в ждущем режиме не более 12 минут. Воспользуемся формулой, известной из теории вероятностей,

,

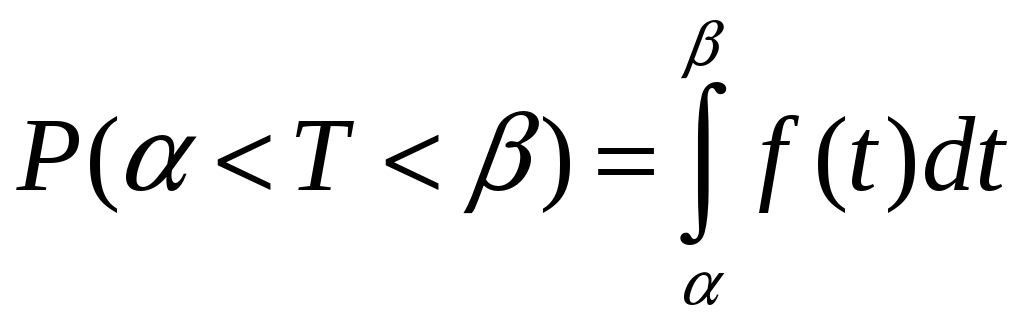тогда имеем

;

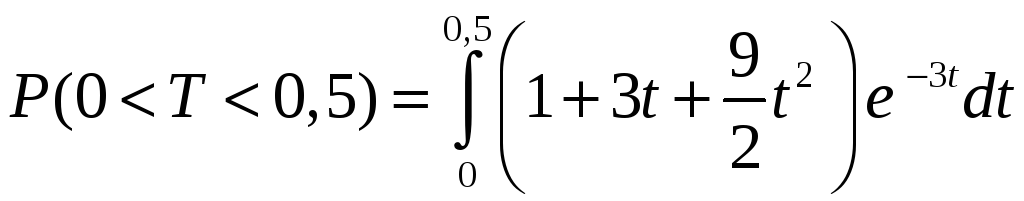Вычислим интеграл с помощью пакета MathCAD

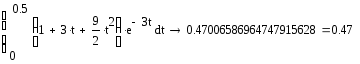
Ответ.

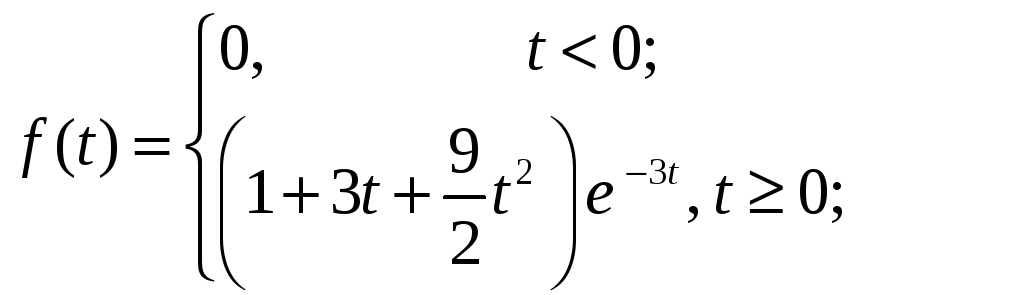
Задача (71–80). Обратить внимание на некоторые изменения в условии задачи!!!

В двухканальную систему массового обслуживания (СМО) с отказами поступает стационарный пуассоновский поток заявок. Время между поступлениями двух последовательных заявок распределено по показательному закону с параметром λ=5 заявок в минуту. Длительность обслуживания каждой заявки равна 0,5 мин. Вновь прибывшая заявка занимает свободный канал с меньшим номером. При занятости всех каналов заявка покидает СМО необслуженной.

Требуется:

1) построить временные диаграммы работы СМО;

2) методом обратных функций смоделировать входящий поток;

2) смоделировать работу СМО методом Монте-Карло, провести три испытания;

3) по результатам трех испытаний найти среднее число обслуженных заявок за время = 4 мин;

Указание: воспользоваться таблицей случайных чисел, приведенной на стр. 24 – 25. В числовых данных задачи: – номер строки, – номер столбца для первого случайного числа. Выбор случайных чисел проводить по строкам, начиная с числа , без пропусков и вставок.

= 5, T = 4, i = 1, j = 1.

Решение. 1) Изобразим статистическое моделирование работы заданной СМО с помощью временных диаграмм. Введем следующие обозначения для временных осей:

Вх – входящий поток заявок, здесь -моменты поступления заявок; T_i – интервалы времени между двумя последовательными заявками. Очевидно, что t_i= t_i-1+Т_i.

К1 – первый канал обслуживания;

К2 – второй канал обслуживания; здесь жирные линии на временной оси обозначают интервалы занятости канала.

Если оба канала свободны, то заявка становится под обслуживание в канал К1, в случае его занятости заявка обслуживается каналом К2.

Если заняты оба канала, то заявка покидает СМО необслуженной.

Вых ОБ – выходящий поток обслуженных заявок.

Вых ПТ – выходящий поток потерянных заявок за счет отказов СМО (случай занятости обоих каналов).

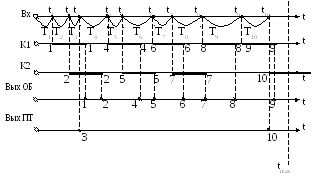
Рис. 1. Временные диаграммы статистического моделирования работы заданной СМО

Статистические испытания продолжаются в течение временного интервала [0; t_max]. Очевидно, что любое превышение времени t_max влечет за собой сброс заявки в выходящий поток Вых ПТ. Так на рис. 1 заявка №10, пришедшая в систему в момент t₁₀, не успевает обслужиться до момента t_max, так как t₁₀+Т_обсл.>t_max. Следовательно, она не принимается свободным каналом К1 на обслуживание и сбрасывается в Вых ПТ, получая отказ.

2) Из временных диаграмм видно, что необходимо научиться моделировать интервалы Т_i. Применим метод обратных функций. Поскольку случайная величина Т_i распределена по показательному закону с параметром λ=5, то плотность распределения имеет вид f(τ)=5е^-5τ . Тогда значение F(T_i) функции распределения вероятностей определяется интегралом

.

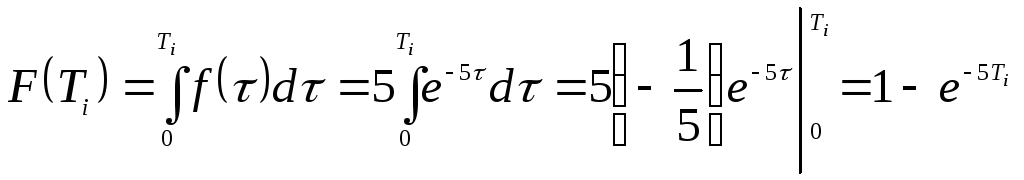Известно, что область значений функции распределения F(T) есть отрезок [0; 1]. Выбираем из таблицы случайных чисел число и определяем Т_i из равенства , откуда . Однако, если . Поэтому можно сразу получать из таблицы случайных чисел реализации . Следовательно, е^-5Тi=r_i , или –5Тi=lnri, откуда .

Результаты вычислений удобно заносить в таблицу.

3) Проведем три испытания для СМО и составим для них три таблицы.

Замечания. 1. Для проведения испытания №1 были взяты случайные числа из приложения 2 на стр. 24 – 25, начиная с первого числа первой строки, первого столбца (первое случайное число строим так: определяем по таблице для i=1,j=1 некоторое число r*=10, тогда искомое случайное число равно r=0,10). Далее выборка осуществлялась по строкам.

2. Проводится три испытания (см. три таблицы).

3. Обратите внимание на выборку случайных чисел из таблицы приложения 2 на стр. 24 – 25, если в испытании №1 последнее случайное число для заявки №16 было 0,37 (первое случайное число во второй строке), то испытание №2 начинается со следующего за ним случайного числа 0,54. Испытание №2 содержит последним случайное число 0,53 (пятое число в третьей строке). Следовательно, третье испытание начнется с числа 0,19. Вообще в пределах одной серии испытаний случайные числа из таблицы выбираются без пропусков и вставок по определенному порядку, например, по строкам.

Таблица 1.

ИСПЫТАНИЕ №1

№ зая-вки i	Сл. число ri	-ln ri	-ln ri= =Тi	Момент поступ-ления заявки ti=ti-1+Ti	Момент окончания обслужив. ti+0,50		Счетчик заявок
					К1	К2	Обсл.	Потер.
	0,10	2,30	0,46	0,46	0,96		1
	0,09	2,41	0,48	0,94		1,44	1
	0,73	0,31	0,06	1,00	1,50		1
	0,25	1,39	0,28	1,28				1
	0,33	1,11	0,22	1,50	2,00		1
	0,76	0,27	0,05	1,55		2,05	1
	0,52	0,65	0,13	1,68				1
	0,01	4,61	0,92	2,60	3,10		1
	0,35	1,05	0,21	2,81		3,31	1
	0,86	0,15	0,03	2,84				1
	0,34	1,08	0,22	3,06				1
	0,67	0,40	0,08	3,14	3,64		1
	0,35	1,05	0,21	3,35		3,85	1
	0,48	0,73	0,15	3,50				1
	0,76	0,27	0,05	3,55				1
	0,37	0,99	0,20	3,75	4,25	STOP
							9

Таблица 2

ИСПЫТАНИЕ №2

№ зая-вки i	Сл. число ri	-ln ri	-ln ri= Тi	Момент поступ-ления заявки ti=ti-1+Ti	Момент окончания обслужив. ti+0,50		Счетчик заявок
					К1	К2	Обсл.	Потер.
	0,54	062	0,12	0,12	0,62		1
	0,20	1,61	0,32	0,44		0,94	1
	0,48	0,73	0,15	0,59				1
	0,05	3,00	0,60	1,19	1,69		1
	0,64	0,45	0,09	1,28		1,78	1
	0,89	0,12	0,02	1,30				1
	0,47	0,76	0,15	1,45				1
	0,42	0,87	0,17	1,62				1
	0,96	0,04	0,01	1,63				1
	0,24	1,43	0,29	1,92	2,42		1
	0,80	0,22	0,04	1,96		2,46	1
	0,52	0,65	0,13	2,09				1
	0,40	0,92	0,18	2,27				1
	0,37	0,99	0,20	2,47	2,97		1
	0,08	2,53	0,51	2,98	3,48		1
	0,42	0,87	0,17	3,15		3,65	1
	0,26	1,35	0,27	3,42				1
	0,89	0,12	0,02	3,44				1
	0,53	0,63	0,13	3,57	4,07	STOP
							9

Таблица №3

ИСПЫТАНИЕ №3

№ зая-вки i		Сл. число ri	-ln ri	-ln ri= Тi	Момент поступ-ления заявки ti=ti-1+Ti	Момент окончания обслужив. ti+0,50		Счетчик заявок
						К1	К2	Обсл.	Потер.
	0,19		1,66	0,33	0,33	0,83		1
	0,64		0,45	0,09	0,42		0,92	1
	0,50		0,69	0,14	0,56				1
	0,93		0,07	0,01	0,57				1
	0,03		3,51	0,70	1,27	1,77		1
	0,23		1,47	0,29	1,56		2,06	1
	0,20		1,61	0,32	1,88	2,38		1
	0,90		0,11	0,02	1,90				1
	0,25		1,39	0,28	2,18		2,68	1
	0,60		0,51	0,10	2,28				1
	0,99		0,01	0,00	2,28				1
	0,01		4,61	0,92	3,20	3,70		1
	0,90		0,11	0,02	3,22		3,72	1
	0,25		1,39	0,28	3,50				1
	0,29		1,24	0,25	3,75	4,25	STOP
								8