Решение:

1) построим график функции в полярной системе координат по точкам, давая  значения через промежуток /8, начиная от =0;

	2	3,24	6,83	26,27	─	26,27	6,83	3,24	2	1,45	1,17	1,04	1	1,04	1,17	1,45	2

2) найдем уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.

Из условия , с другой стороны, , отсюда ; но , следовательно,

Искомое уравнение – это уравнение параболы с вершиной в т. . График пересекает ось Х в т. и

Координаты т. С , т. , т.

Задача 124. Найти указанные пределы, не пользуясь правилом Лопиталя.

а) б)

в) г)

Решение:

а)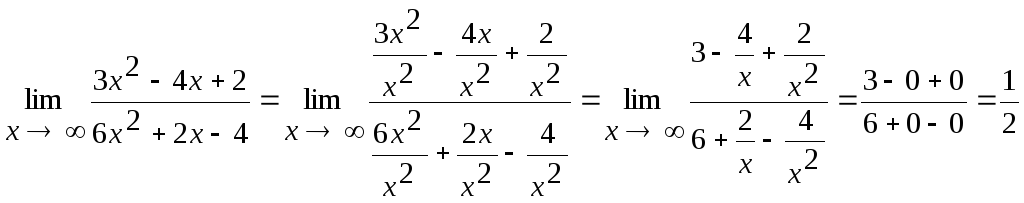

б)

в) Полагая , имеем. Тогда

г)

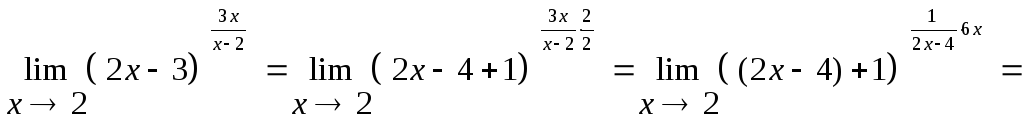
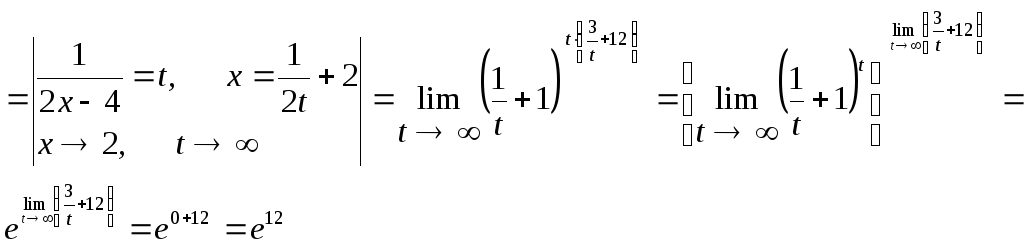
Задача 134. Заданы функция и два значения аргумента и . Требуется:

1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента;

2) в случае разрыва функции найти ее пределы при приближении к точке разрыва слева и справа;

3) сделать схематический чертеж.

Решение:

Функция и неопределенна в т Следовательно в т. разрыва нет, а т. - точка разрыва. Т.к.

и т. не принадлежит области определения функции, то при функция имеет точку разрыва второго рода (бесконечный скачок). Для схематического построения графика функции найдем .

Задача 144. Задана функция различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж.

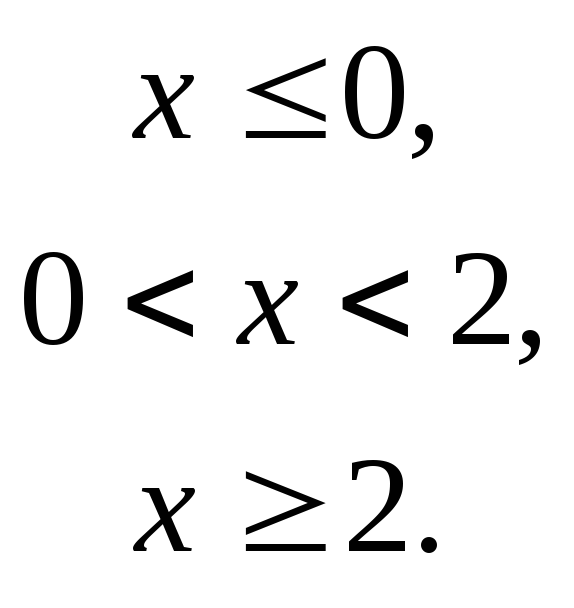
Решение:

Область определения функции - вся числовая ось . Разрывы возможны только в точках и , в которых изменяется аналитическое задание функции.

Найдем односторонние пределы в т. и значение функции в этой точке:

Т.к. в т. функции определена, конечные односторонние пределы существуют и не равны между собой, то т. - точка разрыва первого рода.

Найдем односторонние пределы в т. и значение функции в этой точке:

Т.к. в т. функции определена, конечные односторонние пределы существуют и равны между собой, то в т. функция непрерывна.