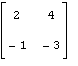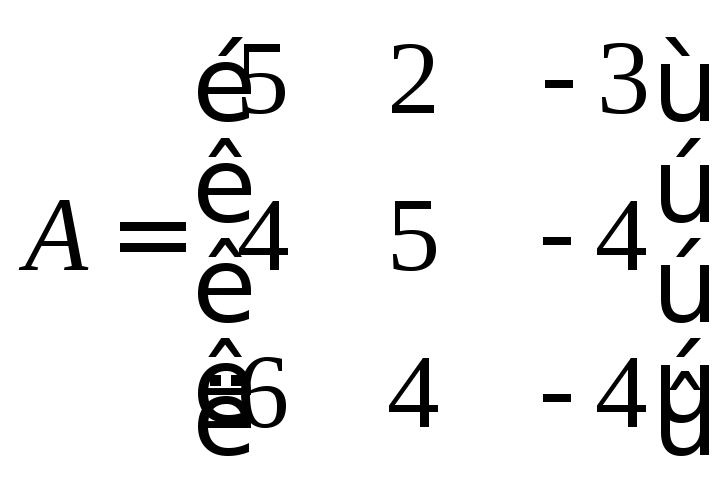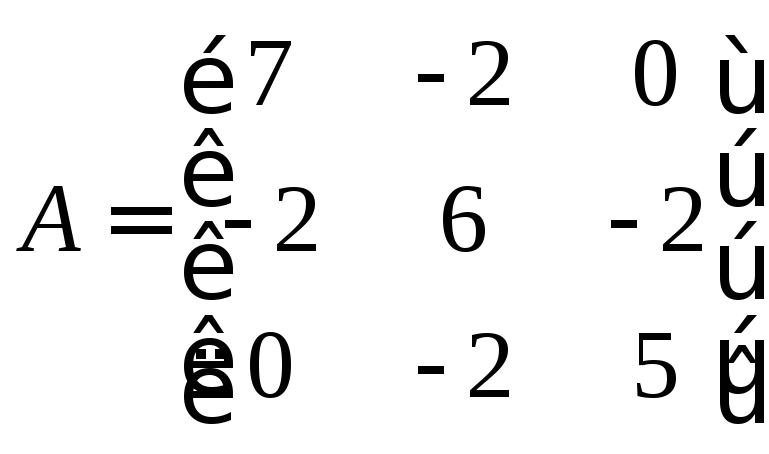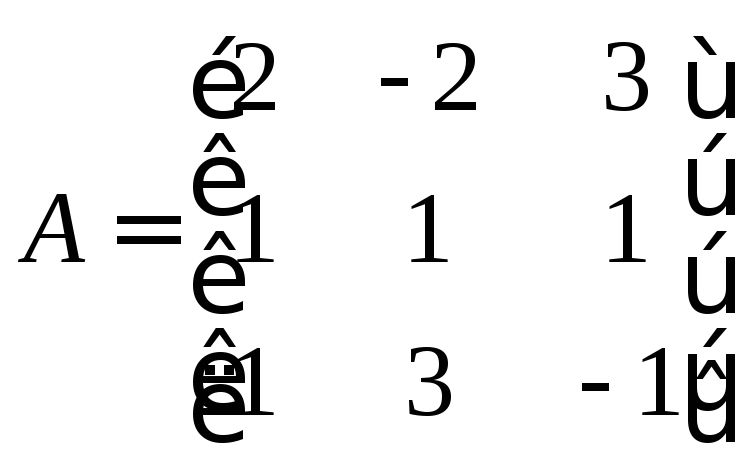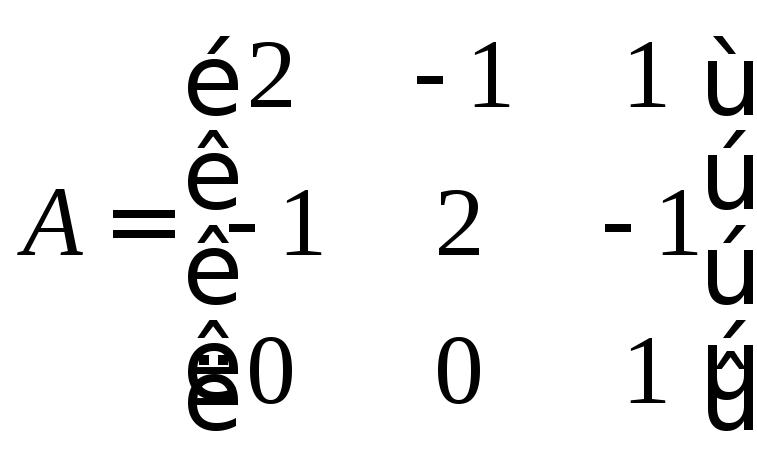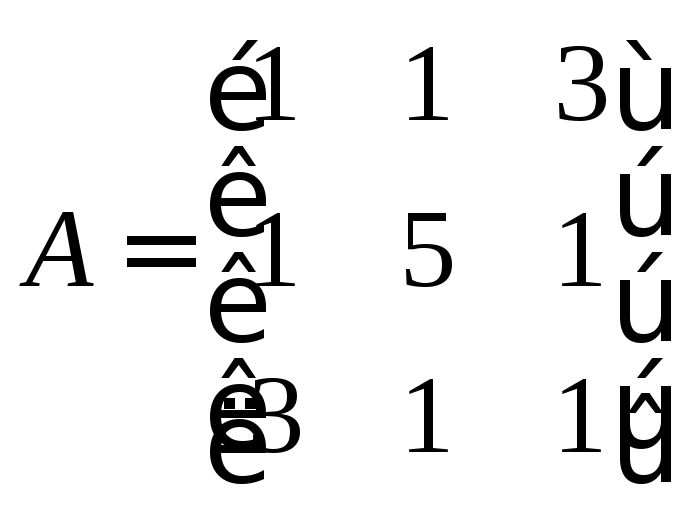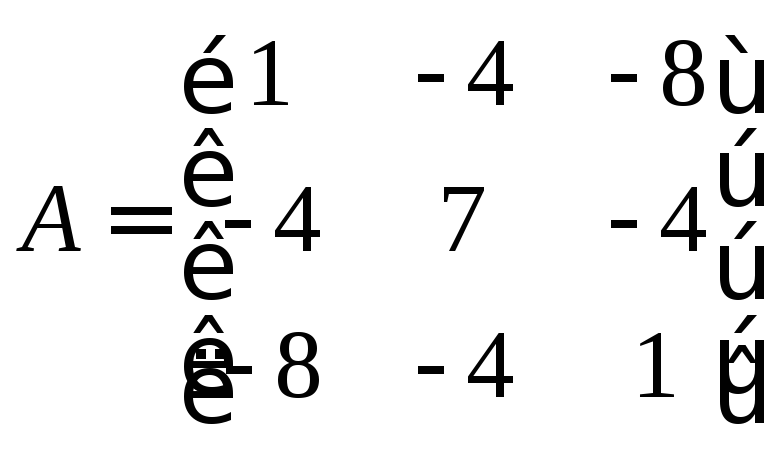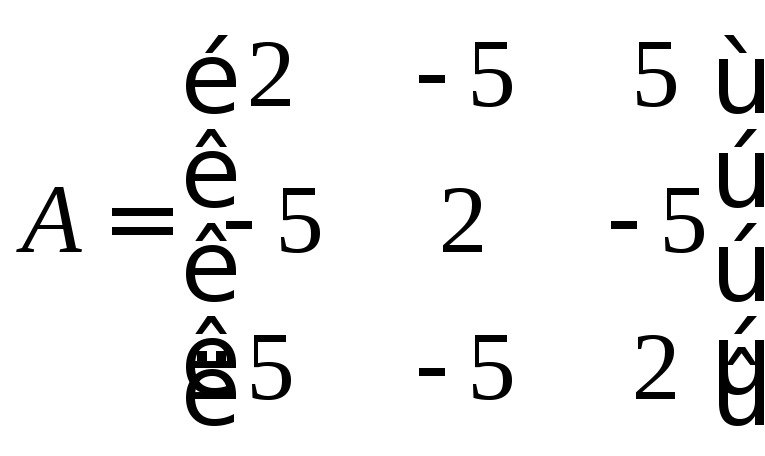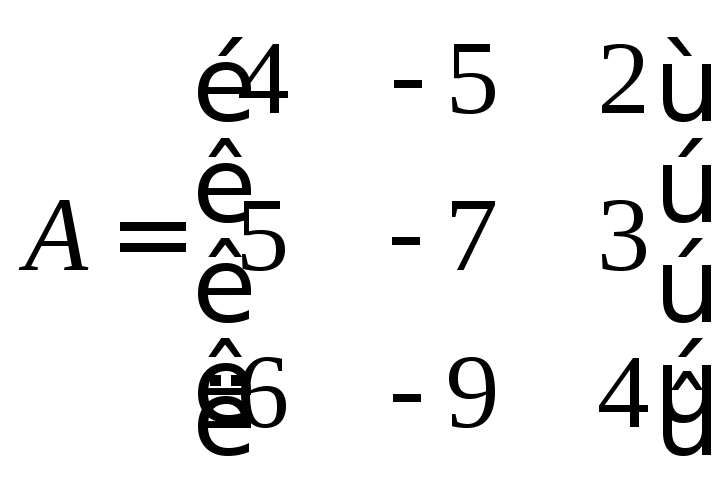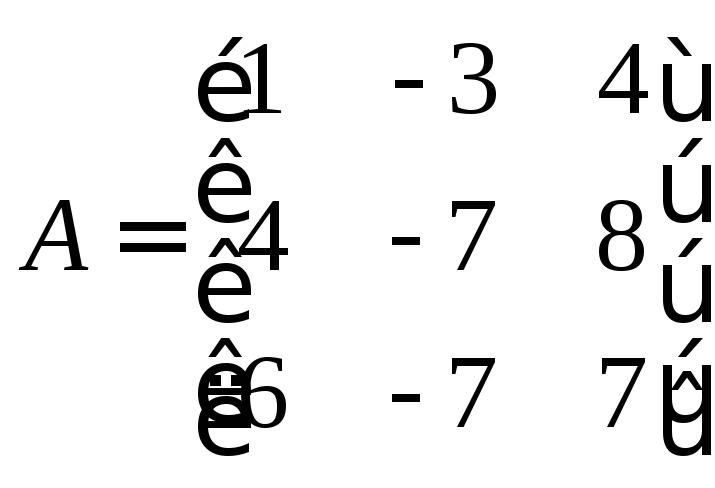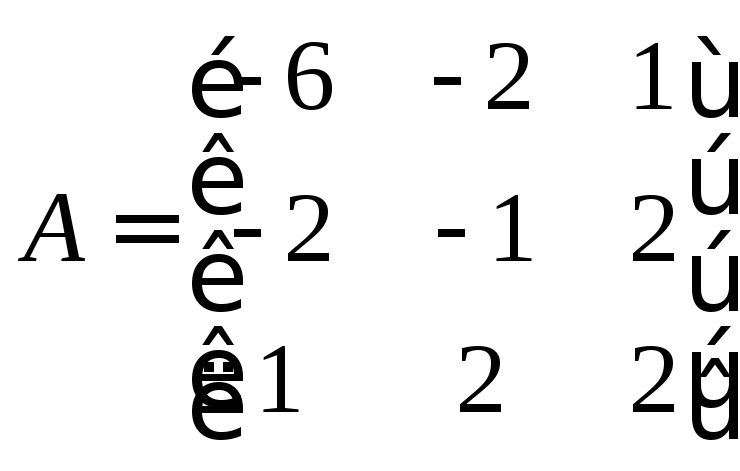71 – 80. Уровень III
Даны векторы
![]() ,
,![]() ,
,![]() ,
,![]() в некотором базисе. Векторы α
в некотором базисе. Векторы α![]() ,β
,β![]() ,γ
,γ![]() и
и![]() образуют замкнутую ломаную линию при
условии, что начало каждого последующего
вектора совмещено с концом предыдущего.
Найти значения чисел α, β, γ.
образуют замкнутую ломаную линию при
условии, что начало каждого последующего
вектора совмещено с концом предыдущего.
Найти значения чисел α, β, γ.
|
71. |
|
|
|
|
|
72. |
|
|
|
|
|
73. |
|
|
|
|
|
74. |
|
|
|
|
|
75. |
|
|
|
|
|
76. |
|
|
|
|
|
77. |
|
|
|
|
|
78. |
|
|
|
|
|
79. |
|
|
|
|
|
80. |
|
|
|
|
Задача 4
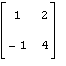
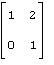
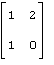
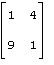
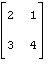
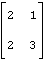
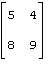
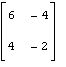
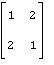
81 – 90. Дана матрица А:
|
81. А= |
|
82. А= |
|
83. А= |
|
84. А= |
|
|
85. А= |
|
86. А= |
|
87. А= |
|
88. А= |
|
|
89. А= |
|
90. А= |
|
|
|
|
|
Уровень I
Найти собственные значения матрицы А.
Уровень II
Найти собственные значения и собственные векторы матрицы А.
Уровень III
Дана матрица А. Найти собственные значения и собственные векторы матрицы А.
|
81. |
|
82. |
|
83. |
|
|
84. |
|
85. |
|
86. |
|
|
87. |
|
88. |
|
89. |
|
|
90. |
|
|
|
|
|
Задача 5
91 – 100. Дана квадратичная форма:
|
91. |
|
92. |
|
|
93. |
|
94. |
|
|
95. |
|
96. |
|
|
97. |
|
98. |
|
|
99. |
|
100. |
|
Уровень I
Написать матрицу квадратичной формы.
Уровень II
Написать матрицу квадратичной формы. Привести квадратичную форму к каноническому виду.
Уровень III
Написать матрицу квадратичной формы. Найти матрицу линейного преобразования, приводящего квадратичную форму к каноническому виду.