III Формула Ньютона-Лейбница для несобственного интеграла 2-го рода

Примем без доказательства теорему, которая упрощает вычисление несобственных интегралов 2-го рода.

Теорема 1. Пусть функция имеет на отрезкеодну или несколько особых точек и пусть– её первообразная, т.е.всюду, за исключением особых точек. Если эта первообразная непрерывна и в этих особых точках, то имеет место формула

.

Примеры. 2. .

3.

4. . Найдем первообразную:

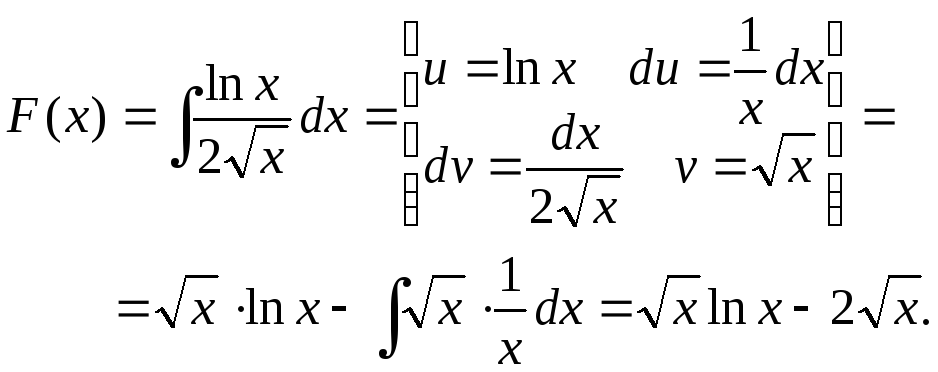
В нуле первообразная не определенна, однако . Положив, мы получим непрерывную напервообразную, поэтому

.

§4. Признаки сходимости несобственного интеграла 2-го рода

Эти признаки совершенно аналогичны признакам сходимости для несобственного интеграла 1-го рода. Приведем лишь их формулировки.

Теорема 1 (1-й признак сравнения). Пусть функции инепрерывны наи– их общая особая точка. Если они удовлетворяют условию, то:

1) из сходимости интеграла от функции следует сходимостьинтеграла от функции;

2) из расходимости интеграла от функции следует расходимостьинтеграла от функции.

Теорема 2 (2-й признак сравнения). Пусть функции инепрерывны и неотрицательны наи– их общая особая точка. Если приэти функции эквивалентны, то несобственные интегралы

и

сходятся или расходятся одновременно.

В качестве эталонного интеграла 2-го рода берут интеграл вида

,

который сходится при , и расходится при .

Примеры. 1. .

При (0 – особая точка) . Кроме тогона. Т.к. интеграл

расходится, то и данный интеграл также расходится.

2. . Особая точка:.

Прежде всего, разложим подкоренное выражение на множители:

.

Теперь нетрудно получить при оценку

=.

Интеграл сходится как эталонный, следовательно сходится и данный интеграл.

Теорема 3 (признак абсолютной сходимости). Если сходится интеграл , то сходится и интеграл(такую его сходимость называ-ют абсолютной).

Пример 3. .

Рассмотрим модуль подынтегральной функции при :

.

Интеграл сходится как эталонный. Последовательно применяя 2-й и 1-й признаки сравнения, получим, чтосходится. Значит, и исходный интеграл сходится, причем абсолютно.

Пример 4. .

Если к этому интегралу применить (незаконно!) свойство линейности, то получим разность двух несобственных расходящихся интегралов. На самом же деле для подынтегральной функции нетрудно получить эквивалент-ность в особой точке. Действительно,

.

Значит, при, и исходный интеграл сходится вместе с эталонным.

§5. Замечания к теме

I Об интегралах смешанного типа

Если на бесконечном промежутке подынтегральная функция имеет особые точки, то интеграл разбивают на сумму отдельных интегралов, пользуясь свойством аддитивности. При этом необходимо, чтобы в каждом таком интеграле была бы одна особая точка, причем она являлась бы пределом интегрирования. Для простоты и бесконечно удаленную точку считаем особой.

Примеры. 1.. Здесь две особые точки:и. Разобьем интеграл на сумму двух:

.

При : , где. Поэтому интегралсходится вместе сдля любого. Если же, то, где. Значит, интегралсходится вместе слишь для. Окончательный вывод: данный интеграл сходится при.

2. Исследуйте самостоятельно интеграл , разбив его на сумму таким образом:

.