– 181–

Тема поверхностные интегралы

§1. Параметрическое задание поверхности

Линию на плоскости можно задавать явно (– парабола), неявно (– лемниската Бернулли) и параметрически – эллипс). Для поверхностей в пространстве мы знакомы с явным заданием– параболоид вращения) и неявным заданием– коническая поверхность). Осталось познакомиться ещё с одним способом – параметрическим.

Сразу заметим, что система трёх однопараметрических уравнений

задаёт в пространстве некоторую линию Для такого задания линии удобно использовать векторную форму записи, а именно: линиясостоит из тех точекрадиус-векторы которых имеют вид

(Подробнее об этом смотри «Математический анализ, ч.1», тема «Функции нескольких переменных»).

Для параметрического задания поверхности необходимы два параметра. Пусть на плоскости с декартовой прямоугольной системой координат в некоторой области заданы три функции Другими словами, каждой точке поставлена в соответствие тройка чисел , которые естественно понимать как координаты точки пространства Множество всех таких точек, и есть некоторая поверхность:

(1)

Здесь также удобна векторная форма записи: поверхность состоит из точек радиус-векторы которых задаются вектор-функцией двух переменных

.

Замечание 1. Исключая из параметрических уравнений оба параметра, можно получить неявное уравнение поверхности и тем самым идентифицировать поверхность.

Пример 1. Уравнения

(2)

определяют сферу .

Пример 2. Уравнения

определяют коническую поверхность

Пример 3. Пусть в плоскости дана окружностьс центром в точке, причёмПри вращении этой окружности вокруг осиполучается поверхность, называемая тором.

Выведем параметрические уравнения тора. Пусть – текущая точка тора. В качестве параметров возьмём два угла:– угол междуи плоскостью,– угол междуи осью, где

Обозначим

Тогда

а

кроме того

Окончательно имеем для тора:

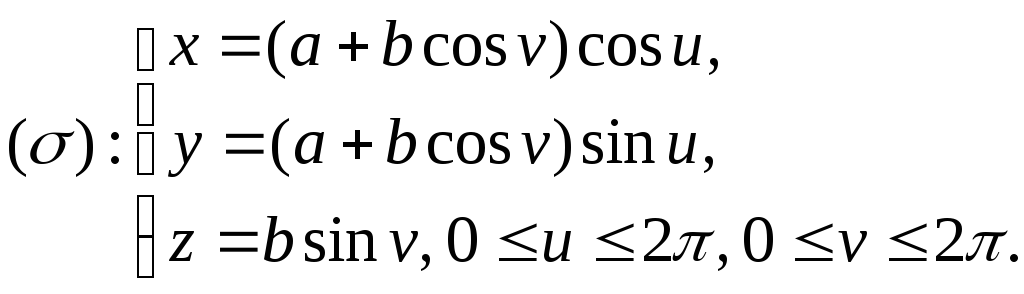
Пример 4. Уравнения

определяют т.н. геликоид (прямой), т.е. поверхность, описываемую прямой , которая вращается вокруг осии одновременно перемещается вдоль этой оси, причем, скорости вращения и перемещения постоянные, в начальный моментсовпадает с

Замечание 2. Явное задание поверхности является частным случаем параметрического:

В параметрических уравнениях (1) зафиксируем значение одного из параметров: пусть, например, Получим систему однопараметрических уравнений

определяющую некоторую линию , которая называется координатной линией. Меняя значение, получим целое семейство таких линий. Аналогично можно получить ещё одно семейство координатных линий:

Через каждую точку (за исключением некоторых точек, таких, как полюса сферы или вершина конуса) проходит по одной линии каждого семейства координатных линий. Соответствующие значения параметров называются криволинейными координатами точки поверхности.

Для сферы (2) координатные линии – это параллели () и меридианы ().

§2. Касательная плоскость к поверхности, заданной параметрически

Напомним, что направляющий вектор касательной к линии

имеет вид . Здесь – значение параметра, которое соответствует точке касания.

Далее, касательная линия к поверхности – это касательная к линии, лежащей на поверхности, а касательная плоскость – это плоскость, в которой лежат все касательные прямые (Подробно обо всём этом смотри «Математический анализ, ч.1», тема «Функции нескольких переменных», §8 и §9).

Что касается нормального вектора касательной плоскости к поверхности

можно рассуждать таким образом. Через точку проходят две координатные линии: и . Их векторные уравнения:

Направляющие векторы касательных к этим линиям и соответственно. Векторное произведение этих векторов

можно взять в качестве нормального вектора касательной плоскости. Зная точку касания , криволинейные координаты которой , и нормальный вектор , нетрудно написать уравнение касательной плоскости

Можно написать готовую формулу касательной плоскости (без вычисления вектора ), если воспользоваться общим приёмом. Берём текущую точку касательной плоскости и рассматриваем три вектора: , и . Они компланарны и, следовательно, их смешанное произведение равно нулю. Отсюда получаем уравнение касательной плоскости

Здесь производные функций вычисляются при значениях параметров и , которые соответствуют точке касания .

Пример. Составить уравнения касательной плоскости к винтовой поверхности

в токе , криволинейные координаты которой .

Решение. Находим частные производные функций и подставляем в соответствующую формулу:

.

Разлагаем определитель по 1^й строке:

.

Оставим в левой части уравнения только члены, содержащие текущие координаты и разделим обе части уравнения на :