
- •Лекция № 41
- •4.6. Лнду-2 с постоянными коэффициентами со специальной правой частью
- •Лекция № 42. Тема 5 : Линейные ду высших порядков
- •5.1. Линейные ду п-го порядка
- •5.2*. Понятие о краевой задаче
- •Лекция № 43. Тема 6 : Системы дифференциальных уравнений
- •6.1. Нормальные системы дифференциальных уравнений
- •6.2. Решение нормальных систем ду методом исключений
Лекция № 41
4.6. Лнду-2 с постоянными коэффициентами со специальной правой частью
Общий вид линейного неоднородного уравнения
![]() ,
(1)
,
(1)
где
![]() .
.
Как известно, общее
решение уравнения (1) имеет вид
![]() .
Рассмотрим, как можно определить частное
решение
.
Рассмотрим, как можно определить частное
решение
![]() в зависимости от вида правой части (1)
в некоторых случаях:
в зависимости от вида правой части (1)
в некоторых случаях:
1.
![]() ,
где
,
где
![]()
многочлен п-ой
степени.
многочлен п-ой
степени.
Зададим вид
частного решения в форме
![]() ,
где
,
где
![]()
многочлен п-ой степени с неопределёнными коэффициентами. Найдём его производные:
![]()
Подставим эти
выражения в уравнение (1) и сократим
на
![]()
![]() .
(2)
.
(2)
Здесь возможны случаи:
1.1. Число
![]() не является корнем характеристического
уравнения, т.е.
не является корнем характеристического
уравнения, т.е.
![]() .
Тогда слева и справа в выражении (2) стоят
многочлены п-ой
степени и, приравнивая коэффициенты
при одинаковых степенях, находим
неопределённые коэффициенты
.
Тогда слева и справа в выражении (2) стоят
многочлены п-ой
степени и, приравнивая коэффициенты
при одинаковых степенях, находим
неопределённые коэффициенты
![]() .
.
1.2. Число
![]() является простым корнем характеристического
уравнения, т.е.
является простым корнем характеристического
уравнения, т.е.
![]() ,
а из теоремы Виета следует
,
а из теоремы Виета следует
![]() .
Тогда слева в выражении (2) стоит многочлен
(п
1)-ой
степени, а справа п-ой
степени. Поэтому, для того чтобы
коэффициенты
.
Тогда слева в выражении (2) стоит многочлен
(п
1)-ой
степени, а справа п-ой
степени. Поэтому, для того чтобы
коэффициенты
![]() были определены, необходимо частное
решение искать в виде многочлена (п
+
1)-ой
степени, но без свободного члена, так
как он исчезает при дифференцировании,
т.е.
были определены, необходимо частное
решение искать в виде многочлена (п
+
1)-ой
степени, но без свободного члена, так
как он исчезает при дифференцировании,
т.е.
![]() .
.
1.3. Число
![]() является двукратным корнем
характеристического уравнения, т.е.
является двукратным корнем
характеристического уравнения, т.е.
![]() ,
а из теоремы Виета следует
,
а из теоремы Виета следует
![]() .
Тогда слева в выражении (2) стоит многочлен
(п
2)-ой
степени, а справа
(п
1)-ой
степени. Рассуждая аналогично, получаем
.
Тогда слева в выражении (2) стоит многочлен
(п
2)-ой
степени, а справа
(п
1)-ой
степени. Рассуждая аналогично, получаем
![]() .
.
Рассмотренные три случая можно объединить общим правилом
Правило 1.
Если правая часть уравнения (1) имеет
вид
![]() ,
то частное решение следует искать в
виде
,
то частное решение следует искать в
виде
![]() ,
где
,
где
![]()
многочлен п-ой
степени с неопределёнными коэффициентами,
а
многочлен п-ой
степени с неопределёнными коэффициентами,
а
![]()
кратность корня
кратность корня
![]() характеристического уравнения.
характеристического уравнения.
Пример 1.
Найти общее решение уравнения
![]()
На предыдущей лекции было найдено общее решение соответствующего однородного уравнения
![]() .
.
Частное решение
будем искать в виде
![]() (случай 1.3).
(случай 1.3).
Подставим это
выражение в наше уравнение и сократим
на
![]() :
:
![]()
или
![]() .
.
Тогда общее решение будет иметь вид
![]()
2.
![]() ,
где
,
где
![]() и
и
![]()
многочлены п-ой
и т-ой
степени соответственно.
многочлены п-ой
и т-ой
степени соответственно.
Частное решение будем искать в виде
![]() ,
,
где
![]() и
и
![]() многочлены с неопределёнными
коэффициентами, а
многочлены с неопределёнными
коэффициентами, а
![]() .
.
Найдём производные:
![]()
![]()
![]()
Если подставить
эти выражения в уравнение (1), сократить
на
![]() и приравнять коэффициенты при
и приравнять коэффициенты при
![]() и
и
![]() ,
то получим систему
,
то получим систему
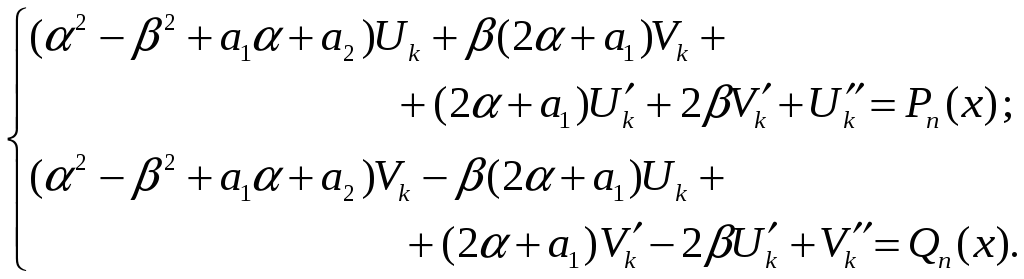 (3)
(3)
Если подставить
числа
![]() в характеристическое уравнение уравнения
(1), то получим
в характеристическое уравнение уравнения
(1), то получим
![]() и тогда возможны случаи:
и тогда возможны случаи:
2.1. Числа
![]() не являются корнями характеристического
уравнения, т.е.
не являются корнями характеристического
уравнения, т.е.
![]() .
.
Тогда слева в
уравнениях (3) стоят многочлены степени
![]() .
Поэтому можно приравнять коэффициенты
при одинаковых степенях х.
В результате получим систему для
определения коэффициентов многочленов
.
Поэтому можно приравнять коэффициенты
при одинаковых степенях х.
В результате получим систему для
определения коэффициентов многочленов
![]() и
и
![]() .
.
2.2. Числа
![]() - корни характеристического уравнения,
т.е.
- корни характеристического уравнения,
т.е.
![]() и
и
![]() .
.
Тогда слева в уравнениях (3) стоят многочлены степени на единицу меньшую, чем k и, рассуждая аналогично, как и ранее, частное решение ищем в виде
![]() .
.
Итак, получаем
Правило 2. Если правая часть уравнения (1) имеет вид
![]() ,
,
то частное решение следует искать в виде
![]() ,
,
если
![]() не
являются корнями характеристического
уравнения, и в виде
не
являются корнями характеристического
уравнения, и в виде
![]() ,
,
если
![]()
корни характеристического уравнения,
где
корни характеристического уравнения,
где
![]() и
и
![]() многочлены с неопределёнными
коэффициентами, а
многочлены с неопределёнными
коэффициентами, а
![]() .
.
Замечание 1.
Правило 2
справедливо и для случая
![]() .
Тогда
.
Тогда
![]()
и, если
![]() корень характеристического уравнения,
то
корень характеристического уравнения,
то
![]()
Замечание 2. Если правая часть уравнения (1) представляет собой сумму двух функций, относящихся к правилам 1-2, то частное решение в силу линейности уравнения ищется в виде суммы двух функций, которые определяются соответственно правилами 1-2.
Пример 2. Найти частное решение уравнения
![]() .
.
Здесь правая часть уравнения представляется в виде суммы двух функций:
![]() и
и
![]() .
.
Поэтому решение
ищем в виде
![]() ,
где
,
где
![]() является частным решением уравнением
является частным решением уравнением
![]() .
(4)
.
(4)
а
![]() является частным решением уравнения
является частным решением уравнения
![]() .
(5)
.
(5)
Для этого случая решение имеет вид (случай 2.1)
![]() .
.
Подставим это выражение в уравнение (4):
![]()
![]() .
.
Сократим на
![]() и приравняем коэффициенты при
и приравняем коэффициенты при
![]() и
и
![]() :
:
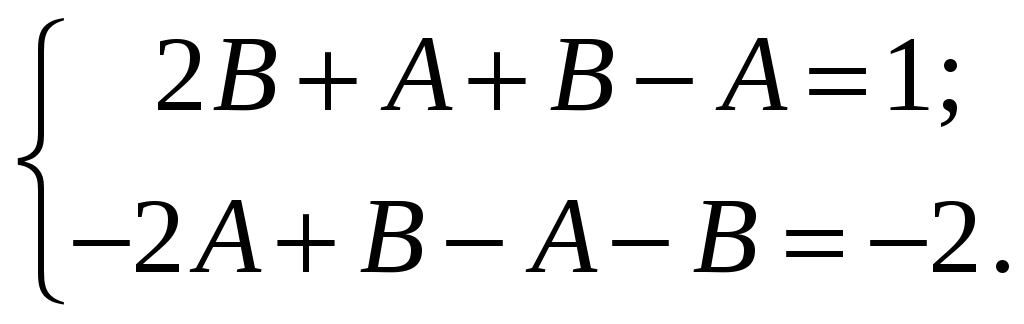
Из решения системы получаем
![]() .
.
Решение уравнения (5) ищем в виде (случай 1.1)
![]() .
.
Подставим это выражение в уравнение (5)
![]() .
.
Приравнивая
коэффициенты при
![]() ,
приходим к системе
,
приходим к системе
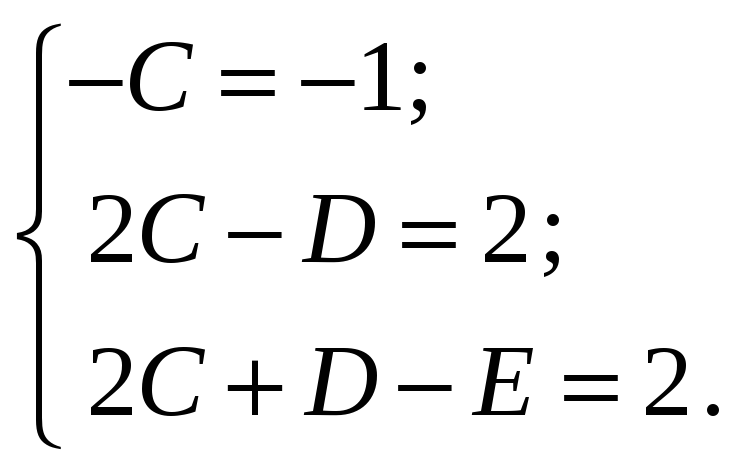
Из решения системы последовательно находим
![]() .
.
Окончательно получим
![]() .
.
