2.2. Основы термодинамики

Средняя кинетическая энергия поступательного движения, приходящаяся на одну степень свободы молекулы,

Средняя энергия молекулы

где i— сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы:

i = n_пост+n_вращ+ 2n_колеб.

Внутренняя энергия идеального газа

,

где v— количество вещества;m— масса газа; М- молярная масса газа;R— газовая постоянная.

Первое начало термодинамики

Q=U+A,

где Q— количество теплоты, сообщаемое системе или отданное ею; U— изменение ее внутренней энергии ; А-работа системы против внешних сил.

Первое начало термодинамики в дифференциальной форме

.

Связь между молярной С_m и удельной с теплоемкостями газа.

С_m=cM,

где М-молярная масса газа.

Молярные теплоемкости газа при постоянном объеме и постоянном давлении

С _v =

Уравнение Майера

С _р= С_v+R.

Изменение внутренней энергии идеального газа

.

Работа, совершаемая газом при изменении его объема,

А=PdV.

Полная работа при изменении объема газа

,

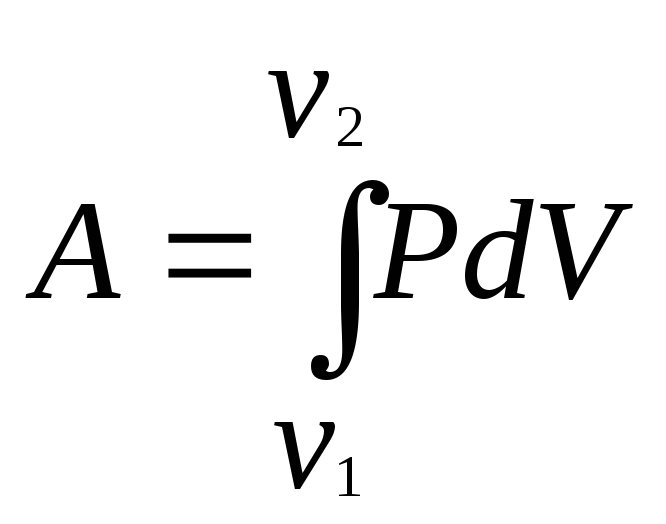где V₁иV₂ — соответственно начальный и конечный объемы газа.

Работа газа:

при изобарном процессе

А =Р(V₂–V₁), или А =;

при изотермическом процессе

А= или А=

Уравнение адиабатного процесса (уравнение Пуассона)

, , ,

где — показатель адиабаты.

Работа в случае адиабатного процесса

А=, или

А=,.

где Т ₁, Т₂иV_1,V₂ —cоответственно начальные и конечные температура и объем газа.

Термический коэффициент полезного действия (КПД) для кругового процесса (цикла)

где Q₁— количество теплоты, полученное системой;Q₂ количество теплоты, отданное системой; А — работа, совершаемая за цикл.

Термический коэффициент полезного действия цикла Карно

где Т₁— температура нагревателя; Т₂— температура холодильника.

Изменение энтропии при равновесном переходе системы из состояния 1 в состояние 2

.

2.3.Реальные газы

Уравнение состояния реального газа ( уравнение Ван-дер-Ваальса) для одного моля

,

где V_m— молярный объем; а иb— постоянные Ван-дер-Ваальса, различные для разных газов.

Уравнение Ван-дер-Ваальса для произвольной массы газа

, или

где =m/М — количество вещества.

Внутреннее давление, обусловленное силами взаимодействия молекул,

Критические параметры — объем V_k, давлениеP_k и температура Т_k— связаны с постоянными а иbВан-дер-Ваальса соотношениями:

V_k =3b,P_k =,T_k=.

Внутренняя энергия 1 моля реального газа

,

где С _м— молярная теплоемкость газа при постоянном объеме.

Примеры решения задач

Задача 1. Во сколько раз плотность воздуха р₁, заполняющего помещение зимой (t₁= 7° С), больше его плотности р₂летом (t₂= 37° С)? Давление газа считать постоянным.

Дано: Р=соnst;t₁=7⁰C;t₂=37⁰C

Определить .

Решение.

Согласно уравнению Менделеева- Клапейрона для первого состояния

(1),

для второго cостояния

(2).

Разделив (1) на (2), при

Р=соnstимеем , откуда,

где T₁=280К; Т₂=310К. Тогда₁/₂= 1,1.

Ответ ₁/₂= 1,1.

Задача 2.Какое число молекулNнаходится в комнате объемомV= 80 м³при температуреt=17°Cи давлении Р = 100 кПа?

Дано: V=80м³;t=17⁰C,T=290K;P=100кПа=10⁵Па.

Определить N.

Решение.

Число молекул N, находящихся в комнате, можно найти из соотношения:N=. Согласно уравнению Менделеева – Клапейрона РV=, откуда. Тогда

Проверим единицы измерения N.

Единиц измерения не имеет.

Подставив числовые значения и вычисляя , получим

N=

Ответ N=2.10²⁷.

Задача 3. Плотность некоторого газа= 0,06 кг/м³, средняя квадратичная скорость его молекул= 500 м/с. Найти давление Р, которое газ оказывает на стенки сосуда.

Дано: = 0,06 кг/м³;=500 м/с

Определить Р.

Решение.

Давление газа определяется основным уравнением молекулярно-кинетической теории (МКТ):

Р = (1),

где n— число молекул в единице объема,m₀— масса молекулы. Кроме того,nиm₀связаны соотношением

n=.

Тогда уравнение (1) можно записать следующим образом

.

Проверим единицы измерения Р.

Подставив числовые значения и вычисляя, получим

Р=.

Ответ Р=5кПа.

Задача 4.Найти внутреннюю энергиюWмассыm=20 г кислорода при температуреt=10° С. Какая часть этой энергии приходится на долю поступательного движения молекул и какая часть на долю вращательного движения?

Дано: m=20=0,02 кг ;t=10⁰C,Т=283К;M=32.10^-3 кг/моль; R=8,31Дж/моль.К

Решение.

Внутренняя энергия кислорода . Здесь число степеней свободы i = 5, из них i = З приходится на долю поступательного движения молекул и i = 2 -на долю вращатель-ного движения. Тогда , , .

Проверим единицы измерения W.

Подставив числовые значения и вычисляя , получим:

W==3,7(кДж);W_пост==2,2(кДж);

W_вращат==1,5( кДж).

Ответ: W=3,7 кДж ;W_пост=2,2 кДж ;W_вращат=1,5кДж.

Задача 5.Энергия поступательного движения молекул азота, находящегося в баллоне объем

V=20 л,W=5 кДж, а средняя квадратичная скорость его молекул=2.10³ м/с. Найти массуmазота в баллоне и давление Р, под которым он находится.

Решение.

Энергия поступательного движения молекул азота откудаm= 2,5 г. Согласно основному уравнениюMKT

— (1),

где n— число молекул в единице объема,m₀— масса одной молекулы. Очевидно, что произведениеnm₀ =— плотности азота. Тогда пm₀ V=V=m— массе всего азота, находящегося в баллоне. Умножив правую и левую части уравнения (1) наV, получим

РV=.

Но , следовательно,

m= 2W/. РV=, откуда Р =.

Проверим единицы измерения mиP.

Подставим числовые значения и вычисляя, получим:

m==2,5.10^-3(кг)

Р=!,67.10⁵=167 (кПа)

Ответ: m=2,5.10^-3кг; Р=167кПа.

Задача 6.Найти удельную теплоемкость с кислорода для: а)V=соnst; б)Р = соnst.

Дано: М=32.10 ^-3кг/моль,і=5,R=8,31Дж/моль.К

Определить: с _v и c_p.

Решение.

Молярная теплоемкость С и удельная теплоемкость с связаны соотношением С = Mс. Отсюда с =. а) ПриV= соnstС_v =. Для кислорода i =5, следовательно, С_v=. Тогда удельная теплоемкостькислорода при постоянном объеме с _v=;

б) При Р = соnstС_p= С_v+R= 7/2R.Отсюда с_p=

Проверим единицы измерения с

Подставив числовые значения и вычисляя, получим:

с _v==650(Дж/кг.К);

с _p==910(Дж/кг.К).

Ответ: с _v=650 Дж/кг.К; с_p=910Дж/кг.К

Задача 7. Найти удельную теплоемкостъ с_pгазовой смеси, состоящей из количестваv₁=3 кмоль аргона и количестваv₂ =3 кмоль азота.

Дано: v₁= v₂=3 кмоль=3.10³моль; М₁=40.10^-3кг/моль; М₂=28.10^-3кг/моль;R=8,31Дж/моль.К

Определить с_p.

Решение.

Количество тепла, необходимое для нагревания смеси газов на некоторую температуру Т

Q= с_p(m₁+m₂)T

или Q=(c_p1m₁+ с_p2m₂)Т. Тогда с_p(m₁+m₂)Т =( с_p1m₁+c_p2m₂)T,

отсюда

.

Т. к. аргон — газ одноатомный, то число степеней свободы i=3,aазот — двухатомный, поэтомуi= 5.

Т.к. ,

то и .

Тогда теплоемкость смеси при Р= cоnst:

Проверим единицы измерения с_p.

Подставив числовые значения и вычисляя, получим:

=733( Дж/кг.К.)

Ответ c_p =733 Дж/кг.К.

Задача 8. Какая часть молекул азота приt=150° С обладает скоростями от 300 до 325 м/с?

Дано: t=150° С, Т=423К;v₁=300 м/с ;v₂=325 м/с ; М=28.10^-3кг/моль;R=8,31 Дж/моль.К

Определить .

Решение.

Из закона Максвелла имеем

(1),

где относительная скорость

u=v₁/ v_в (2),

u=(3).

Здесь v_в=(4) — наиболее вероятная скорость молекул. Решая совместно уравнения (1) — (4), получим

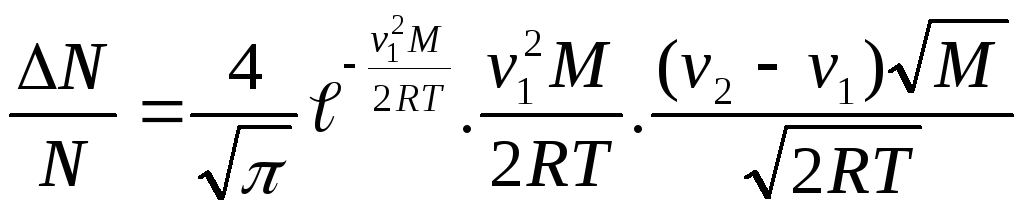
Подставив числовые значения и вычисляя, получим

=

2,8%.

Ответ =2,8%.

Задача 9.Какую массуmуглекислого газа можно нагреть при Р= соnstот температурыt₁= 20°С доt₂=100°С количеством теплотыQ= 222 Дж? На сколько при этом изменится кинетическая энергия одной молекулы?

Дано: Р=соnst;t₁=20⁰C, Т₁=293К ;t₂=100⁰C, Т₂=373К ;Q=222Дж.

Определить: m;W.

Решение.

Количество тепла Q=c_p mТ .

Теплоемкость при Р=соnst:

. Молярная масса М=М_с+2М_{о .} Т.к.СО₂-газ трехатомный,тоi=6.

Тогда Откуда

Значит, .

Кинетическая энергия поступательного движения молекул

, приi=6:W₁=3KT₁;W₂=3kT₂. ТогдаW=W₂-W₁=3k(T₂-T₁)

Проверим единицы измерения mиW.

Подставив числовые значения и вычисляя, получим:

m==3,67 .10^-3(кг) =3,67г.

W=3.1,38.10^-23(373-293)=3,31.10^-21(Дж).

Ответ: m=3,67г ;W=3,31.10^-21Дж.

Задача 10.На какой высотеhплотность газа вдвое меньше его плотности на уровне моря? Температуру газа считать постоянной и равнойt= 0° С. Задачу решить для воздуха.

Дано: t=0⁰ C,Т=273К; М=29.10^-3кг/моль;g=9,8м/с² ;R=8,31Дж/моль.К.

Решение.

Cогласно барометрической формуле. Из уравнения Менделеева –Клапейронаимеем. Следовательно плотность газа на уровне моря

и на высоте hсоответственно равны: и

По условию задачи илиПрологарифмируем полученное выраже-ние, отсюда.

Проверим единицы измерения h.

Подставив числовые значения и вычисляя, получим =5,53.10^-3( м) =5,53(км).

Ответ h=5,53 км.

Задача 11.Работа изотермического расширения массыm= IОг некоторого газа от объема

V₁ доV₂= 2V₁оказалась равной А = 575 Дж. Найти среднюю квадратичную скоростьv_кв

молекул газа при этой температуре.

Дано: m= I0г=0,01кг;V₂= 2V₁; А = 575 Дж.

Определить v_кв.

Решение.

Работа по расширению газа А=РdV, откуда А =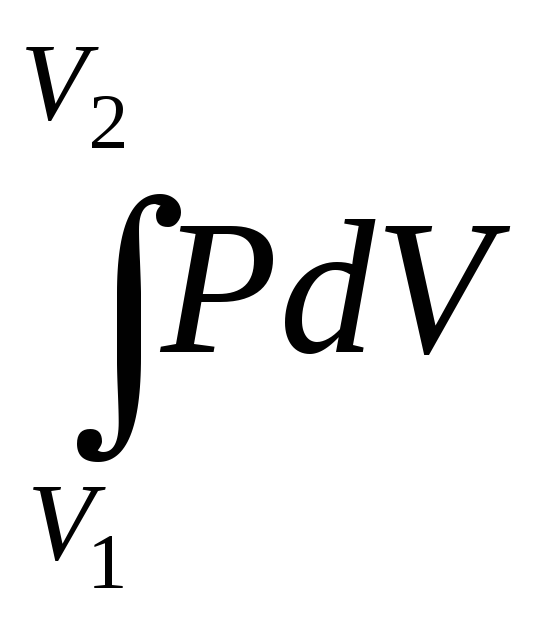. Согласно уравнению Менделеева — Клапейрона , следовательно, Р =. Тогда работа

А=.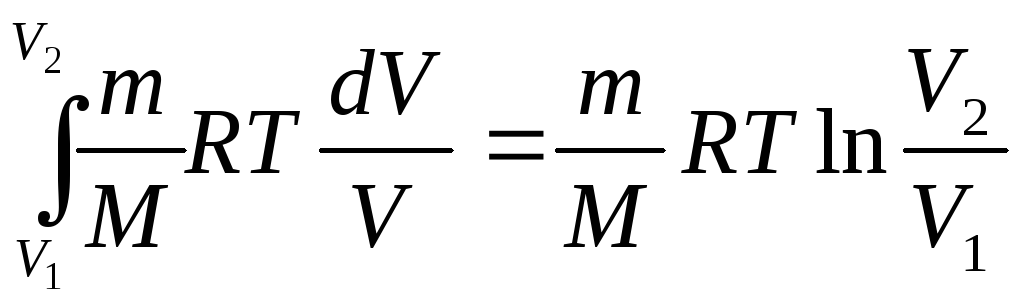

Откуда выразим температуру

T=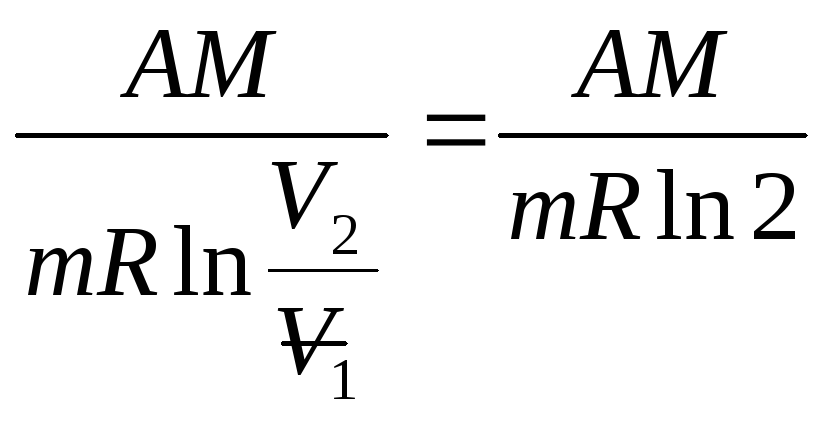(1).

Средняя квадратичная скорость молекул v_кв=. Из (1), тогда

v_кв=.

Проверим единицы измерения v_кв.

Подставив числовые значения и вычисляя , получим

Ответ v_кв=500м/с.

Задача12. Газ расширяется адиабатически так, что его давление падает от Р₁=2ООкПа до Р₂=I00кПа. Затем он нагревается при постоянном объеме до первоначальной температу-ры, причем его давление становится равным Р =122 кПа. Найти отношение с_p/c_vдля этого газа. Начертить график этого процесса.

Дано: Р₁=200кПа; Р₂=I00кПа; Р =122 кПа.

Определитьс_p/c_v.

Р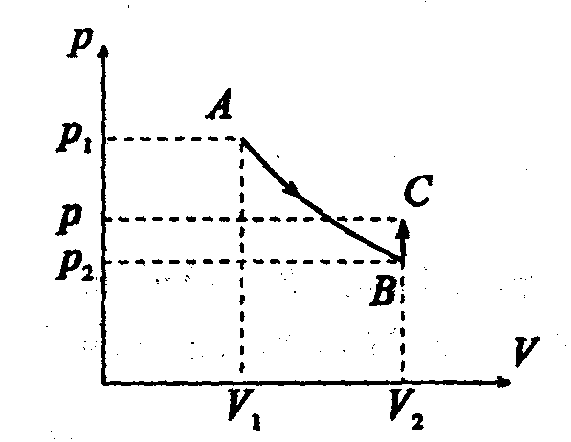ешение.

Из уравнения Пуассона

Т.к.V=const, тоили

. ТогдаРис.1.

Прологарифмируем полученное выражение

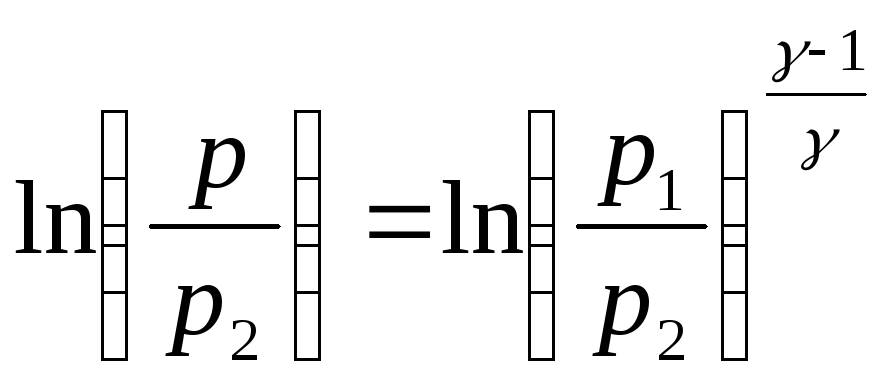или. Отсюдаили

. Окончательно получим

Подставив числовые значения и вычисляя, получим

График процесса представлен на рисунке 1, где АВ адиабата , ВС изохора.

Ответ 1,4.

Задача13. Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу А = 2,94 кДж и отдает за один цикл холодильнику количество теплотыQ₂=13,4 кДж. Найти КПДцикла.

Дано: А = 2,94 кДж=2,94.10 ³Дж ;Q₂=13,4кДж=1,34.10⁴Дж

Определить.

Решение.

КПД цикла Карно =(1),

где Q₁— количество тепла, подведенного к рабочему телу. Т. к. по условию машина является идеальной, то

==(2).

Сравнивая выражения (1) и (2), получим А = Q₁ - Q_{2 ,} откудаQ₁ =А+Q₂.Тогда=

Подставив числовые значения и вычисляя, получим

=

Ответ =18%.

Задача14. Найти изменениеSэнтропии при превращении массыm=10г льда

(t=-20⁰ C) в пар (t_п=100°С).

Дано: m=10г=0,01кг;t=-20⁰ C, Т=253К;t_п=100°С, Т=373К.

Определить S..

Решение.

Изменение энтропии при переходе вещества из состояния 1 в состояние 2

.

При переходе из одного агрегатного состояния в другое, общее изменение энтропии складывается из изменений ее в отдельных процессах. При нагревании льда от Т до Т₀

(Т ₀— температура плавления льда) .

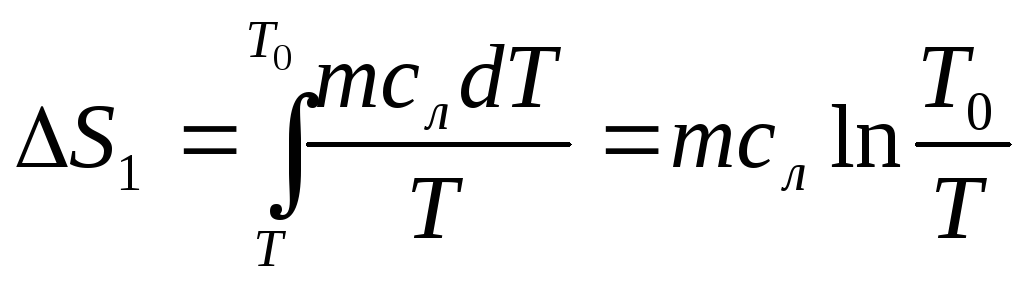, где с = 2,1кДж/(кг.К) —удельная теплоемкость льда.

При плавлении льда

, где-удельная теплота плавления.

При нагревании воды от Т₀ до Т_п

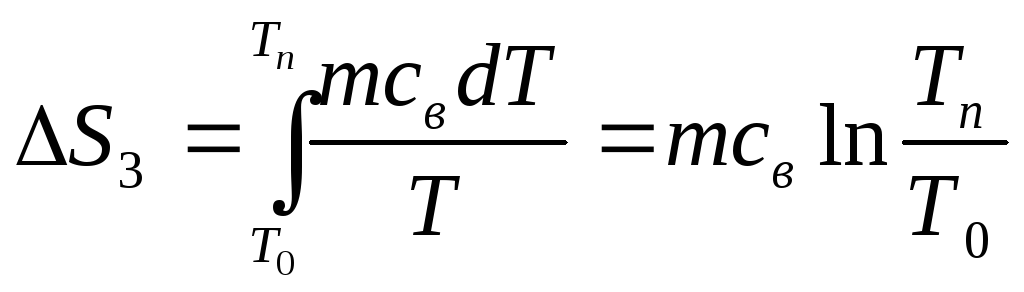, где с_в=4,19кДж/(кг.К) – удельная теплоемкость воды.

При испарении воды при температуре Т _п

_,гдеr=2,26MДж/кг -удельная теплота парообразования _.

Общее изменение энтропии

Проверим единицы измерения S.

Подставив числовые значения и вычисляя, получим

(Дж/К).

Ответ S=87,36Дж/К.

Задача 15. Массаm=10,5 г азота изотермически расширяется от объемаV₁=2 л до объема

V₂=5 л. Найти изменение Sэнтропии при этом процессе.

Дано: m=10,5 г=10,5.!0^-3кг;V₁=2 л=2.10^-3м³;V₂=5 л=5.10^-3м³; М=28.10^-3кг/моль.

Определить S.

Решение.

Изменение энтропии S=5, гдеQ= РdVпри изотермическом процессе. Из

уравнения Менделеева — Клапейрона РV=давление Р =, тогда

, а изменение энтропии

. Проверим единицы измеренияS.

Подставив числовые значения и вычисляя, получим

Ответ S= 2,85Дж/К.

Задача16.Некоторый газ (v= 1 кмоль) занимает объемV₁=1 м³. При расширении газа до объемаV₂= 1,5 м³была совершена работа А против сил межмолекулярного притяжения, равная 45,3 кДж. Определять поправкуа, входящую в уравнение Ван-дер-Ваальса.

Дано: v= 1 кмоль =10³моль,V₁= 1м³,V₂= 1,5 м3, А= 45,ЗкДж=4,53.10⁴Дж.

Определить а.

Решение.Работа, совершаемая против сил межмолекулярного притяжения,

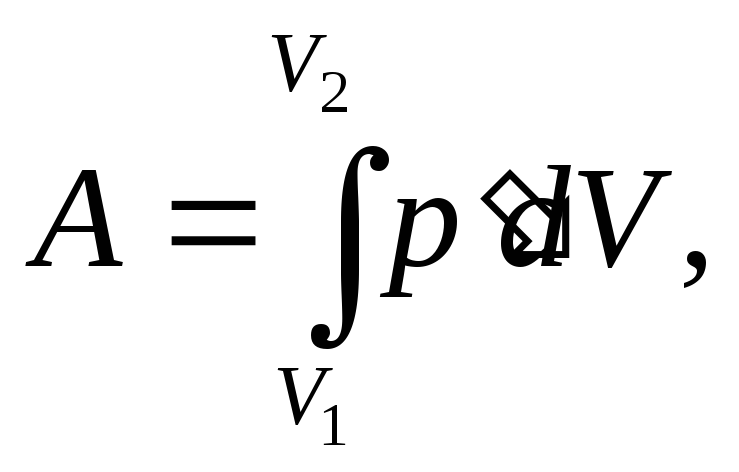
где - внутреннее давление, обусловленное силами взаимодействия молекул. Таким образом,

Откуда

Проверим единицы измеренияа.

Подставив числовые значения и вычисляя , получим

=0,136(Н.м⁴/моль²)

Ответ a=0,136Н.м⁴/моль²

Задачи

2.1. Подсчитать при постоянном давлении удельную теплоемкость газовой смеси, состоящей из 20 г водорода и 1 кг кислорода.

2.2. В закрытом сосуде емкостью 2 м³находится 1,2 кг азота и 2 кг гелия. Определить температуру газовой смеси и парциальное давление гелия, если парциальное давление азота равно 1,2. I0⁵ Па.

2.3. Вычислить удельную теплоемкость при постоянном объеме смеси состоящей из

0,2 кг аргона и 0,1 кг гелия.

2.4. Средняя квадратичная скорость молекул некоторого газа 200 м/с. Давление газа равно 2,5 10 ⁵Па. Найти плотность газа при этих условиях.

2.5. Чему равна энергия вращательного движения молекул, содержащихся в 0,2 кг водо-рода при температуре 400С.

2.6. Найти кинетическую энергию теплового движения молекул, находящихся в 0,05 кг воздуха при температуре 20⁰ С. Воздух считать однородным газом, масса 1 кгмоль кото-рого равна 29 кг/кмоль.

2.7. Чему равна энергия теплового движения молекул двухатомного газа, заключенного в сосуд объемом 0,02 м ³и находящийся под давлением 3.I0⁵Па?

2.8. Средняя квадратичная скорость молекул некоторого газа при нормальных условиях равна 450 м/с. Какое количество молекул содержится в 0,001 кг этого газа?

2.9. Найти отношение средних квадратичных скоростей молекул водорода и гелия при одинаковых температурах.

2.10. Плотность некоторого газа равна 5.I0 ^-2 кг/м³, средняя квадратичная скорость моле-кул этого газа равна 500 м/с. Найти давление, которое оказывает газ на стенки сосуда.

2.11. В баллоне находится газ (водород) под давлением 4.10 ⁵Па при температуре 20°С.

Вычислить плотность газа и концентрацию молекул.

2.12. Чему равна энергия теплового движения молекул двухатомного газа заключенного в сосуд объемом 2 м ³и находящегося под давлением б.I0⁵Па?

2.13. Какая часть молекул азота при 27°С обладает скоростями, находящимися в интер-вале от 50 до 60 м/с?.

2.14. Какая часть молекул водорода при 50°С обладает скоростями от 1000 до 1100м/с?

2.15. Наиболее вероятная скорость молекул кислорода при давлении 0,5.10 ⁵Па равна

200 м/с. Чему равно число молекул в единице объема?

2.16.Определить внутреннюю и кинетическую энергии вращательного движения молекул, содержащихся в 1 кг кислорода при температуре 57°С.

2.17. Вычислить кинетическую энергию поступательного, вращательного движения и полную кинетическую знергию молекул аргона, кислорода и паров воды при температуре 37°С, а также наиболее вероятные скорости.

2.18. В сосуде находится азот, молекулы которого движутся со средней квадратичной скоростью 200 м/с. Вычислить среднюю кинетическую энергию поступательного и вра-щательного движения молекул.

2.19. Баллон емкостью 0,02 м ³содержит 0,02 кг водорода и 0,01 кг гелия при температуре 17°С. Определить давление смеси газов.

2.20. Чему равны удельные теплоёмкости c_v некоторого двухатомного газа если плотность

этого газа при нормальных условиях равна 1,43 кг /м ³?

2.21. На какой высоте плотность газа составляет 50% от плотности его на уровне моря? Температуру считать постоянной и равной 0 ⁰С.Задачу решить для воздуха.

2.22. На какой высоте давление воздуха составляет 25% от давления на уровне моря ?

Температуру считать постоянной и равной 0 ⁰С

2.23. Найти коэффициент внутреннего трения азота при нормальных условиях, если козф-фицент диффузии для него при этих условиях равен 1,4. I0 ^-5м²/с.

2.24. Найти коэффициент теплопроводности азота при температуре 20 ⁰ С и давлении

2.10 ⁵Па. Диаметр молекулы принять равным 3.10^-10м.

2.25. Водород и азот находятся при одинаковых температуре и давлении. Найти для этих газов отношение: i) коэффициентов диффузии; 2) коэффициентов внутреннего трения;

3) коэффициентов теплопроводности d_азот= 3.10^-10 м;d_{водород}= 2,3.I0^-10м.

2.26. Водород при давлении 2.I0 ⁵Па имеет среднюю квадратичную скорость 200 м/с. Определить среднюю длину свободного пробега.

2.27. Молекулы азота обладают средней арифметической скоростью 1000 м/с при нор-мальном давлении. Определить число столкновений в 1 с.

2.28. Определить число столкновений между молекулами, которые произойдут в течение

I с в 1 см ³азота, имеющего при температуре 17°С давлеие 2. I0⁵Па.

2.29. Средняя длина свободного пробега молекул кислорода при нормальных условиях равна 6. 10 ^-6м. Вычислить среднюю арифметическую скорость молекул и число соуда-рений в 1 с.

2.30. При каком давлении средняя длина свободного пробега молекул кислорода равна 2,0 .I0 ^-2м, если температура 17⁰С ?

2.31. Какова плотность воздуха, если средняя длина свободного пробега молекул равна

0,3 м?

2.32. Найти среднюю длину свободного пробега молекул воздуха при температуре 27 ⁰С и давлении 2,0. 10⁵Па, если эффективный диаметр молекул воздуха равен 3.0 10^-10м.

2.33. Вычислить диаметр молекулы азота, если известно, что при температуре 0 ⁰ С и дав-лении 1 атм коэффициент внутреннего трения равен 1,66.10^-5кг.м^-1с^-1.

2.34. Во сколько раз коэффициент теплопроводности водорода больше , чем кислорода при той же температуре и давлении?

2.35. Водород при давлении 1,5. I0 ⁵Па имеет среднюю квадратичную скорость 500 м/с. Определить среднюю длину свободного пробега молекул.

2 36. Аргон находится в сосуде при температуре I 7 ⁰ С и давлении 1,1 10⁵Па. Вычислить среднюю длину свободного пробега молекул.

2.37. 2 кгмоль аргона нагревают при изобарическом процессе на 57°С. Определить изме-нение внутренней энергии газа.

2.38. 1 кг водорода при температуре 27°С изотермически расширили до двойного объема, а затем изохорически охладили, уменьшив давление в 5 раз. Дать схему кривых в системе координат Р и V. Подсчитать изменение внутренней энергии и внешнюю работу газа.

2.39 1 кг кислорода охлаждают от 75 до 25°С при постоянном давлении. Определить изме-нение внутренней энергии, внешнюю работу газа и количество выделенного тепла.

2.40. 5.I0 ^-3м³воздуха, содержащиеся в сосуде при нормальных условиях, расширяют при постоянном давлении до двойного объема, а затем адиабатически расширяют так, что дав-ление становится в 4 раза меньше, чем первоначальное. Вычислить работу расширения га-за при этих условиях.

2.41. Кгмоль азота при температуре 20 ⁰ С и давлении 2.I0⁵Па расширяют в первом слу-чае изотермически, а во втором случае адиабатически, конечное давление равно 1.10⁵Па. Найти работу расширения газа при изотермическом и адиабатическом процессе.

2.42. Аргон при давлении 2. 10 ⁵Па изменил объем с 2 м³до 4 м³. Как изменится вели-чина внутренней энергии, если расширение проводилось адиабатически?

2.43. Метан, занимавший объем 10 ^-2 м³и находящийся под давлением 15. 10⁵Па, был

нагрет от 10 до 27⁰С при постоянном давлении. Определить работу расширения газа и изменение его внутренней энергии.

2.44. При постоянном давлении 1 кмоль азота был нагрет на 150 ⁰С. Определить коли-чество теплоты, переданной газу, работу расширения и изменение внутренней энергии газа.

2.45. При адиабатическом расширении 0,2 кг азота при температуре 27°С, объем газа уве-личился в 10 раз. Определить конечную температуру газа и работу расширения.

2.46. Какая работа затрачивается при изотермическом сжатии 0,50 кг воздуха, взятого при температуре 17⁰С, если объем газа уменьшается в 5 раз?

2.47. Сколько теплоты поглощается при изотермическом расширении 10 ^-2м³газа, находя-щегося под давлением 10⁵Па до объема I,5.10^-2м³?

2.48. После адиабатического сжатия 7 кг азота, имеющего температуру-13°С и объем

0,2 м ³, его температура стала 227°С. Каково давление азота после сжатия? Какая работа была затрачена при сжатии газа?

2.49. При изотермическом расширении 0,1 кг азота, находящегося при температуре 17 ⁰С, была совершена работа, равная 860 Дж. Во сколько раз изменилось давление азота при расширении?

2.50. Работа изотермического расширения 0,1 кг некоторого газа от объема V₁до объемаV₂= 2V₁, равна 575 Дж. Найти среднюю квадратичную скорость молекул газа при этой температуре.

2.51. При изтермическом расширении 2 м ³газа давление его меняется от Р₁= 5 атм до

Р₂= 4 атм. I атм = I.10⁵Па. Найти совершенную при этом работу.

2.52. Газ расширяется адиабатически так, что его давление падает от 2.10 ⁵Па до 1.I0⁵Па. Затем он нагреваетса при постоянном объеме до первоначальной температуры, причем его давление возрастает до 1,22. I0⁵Па. Определить отношение С_р/ С_Vдля этого газа. Начер-тить график этого процесса.

2.53. При адиабатическом сжатии 1 кмоль двухатомного газа была совершена работа в

46 кДж. На сколько увеличилась температура газа.

2.54. 7.10 ^-3кг углекислого газа было нагрето на 100 в условиях свободного расширения. Найти работу расширения газа и изменение его внутренней энергии.

2.55. Газ, занимающий объем 5.10 ^-3м³ и находящийся под давлением 2.10 ⁵Па при тем-пературе 17⁰ С был нагрет и расширялся изобарически. Работа расширения газа при

этом оказалась равной 200 Дж. На сколько нагрели газ?

2.56. Считая азот идеальным газом, определить его удельную теплоемкость: 1) для

изобарного процесса; 2) для изохорного процесса.

2.57. Определить удельные теплоемкости c_vи с_p, некоторого газа, если известно, что его удельный объем при нормальных условияхV= 0,7 м³/кг. Что это за газ?

2.58. Определить удельные теплоемкости с _v, и с_p, смеси углекислого газа массойm₁= 3 г и азота массойm₂=4 г.

2.59. Определить показатель адиабаты у смеси газов, содержащей гелий массой m₁=8 г и водород массойm₂=2 г.

2.60. Применяя первое начало термодинамики и уравнение состояния идеального газа, показать , что разность удельных теплоемкостей с_p - с_v =R/M.

2.61. Кислород массой 32 г находится в закрытом сосуде под давлением 0,1 МПа при

температуре. 290 К. После нагревания давление в сосуде повысилось в 4 раза. Опреде-лить: 1) объем сосуда; 2) температуру, до которой газ нагрели; 3) количество теплоты, сообщенное газу.

2.62.Определить количество теплоты, сообщенное газу, если в процессе изохорного нагревания кислорода объемом V=20 л его давление изменилось нар = 100 кПа.

2.63. Двухатомный идеальный газ (v=2 моль) нагревают при постоянном объеме до температуры Т₁= 289 К. Определить количество теплоты, которое необходимо сооб-

щить газу ,чтобы увеличить его давление в n=3 раза?

2.64. При изобарном нагревании некоторого идеального газа (v=2 моль) на Т =90 К ему было сообщено количество теплоты 5,25 кДж. Определить: 1) работу, совершаемую газом; 2) изменение внутренней энергии газа; З) величинуС_p/С_v.

2.65. Азот массой m= 280 г расширяется в результате изобарного процесса при давления

Р = 1 МПа. Определить: 1) работу расширения А; 2) конечный объем V₂газа, если на расширение затрачена теплотаQ=5 кДж, а начальная температура азота Т₁= 290 К.

2.66. Кислород объемом 1 л находится под давлением 1 МПа. Определить, какое коли-чество теплоты необходимо сообщить газу, чтобы: 1) увеличить его объем вдвое в ре-зультате изобарного процесса; 2) увеличить его давление вдвое в результате изохорного процесса.

2.67. Некоторый газ массой m=5 г расширяется изотермически от объемаV₁до объема

V₂= 2V₁. Работа расширения А = 1 кДж. Определить среднюю квадратичную скорость молекул газа.

2.б8 Азот массой m=14 г сжимают изотермически при температуре Т₁=300 К от дав-ления Р₁= 100 кПа до давления Р₂= 500 кПа. Определить: 1) изменение внутренней энергии газа; 2) работу сжатия; З) количество выделившейся теплоты.

2.69. Работа расширения некоторого двухатомного идеального газа составляет А =2 кДж.

Определить количество подведенной к газу теплоты, если процесс протекал: 1) изотер-мически; 2) изобарно.

2.70. При адиабатном расширении кислорода ( v=2 моль), находящегося при нормальных условиях, его объем увеличился вn= З раза. Определить: 1) изменение внутренней энер-гии газа; 2) работу расширения газа.

2.71. Азот массой m= 1 кг занимаёт при температуре Т₁= 300 К объемV₁= 0,5 м³. В

результате адиабатного сжатия давление газа увеличилось в З раза. Определить: 1)конеч-ный объем газа; 2) его конечную температуру; З) изменение внутренней энергии газа.

2.72. Азот, находившийся при температуре 400 К, подвергли адиабатному расширению, в результате которого его объем увеличился в n= 5 раз, а внутренняя энергия уменьшилась на 4 кДж. Определить массу азота.

2.73. Идеальная тепловая машина работает по циклу Карно. Определить КПД цикла, если известно, что за один цикл была произведена работа, равная 3.10 ⁴Дж, и холодильнику было передано 13.10⁴Дж.

.

2.74. Идеальная тепловая машина, работающая по циклу Карно, совершает за один цикл работу 7,35.10⁴ Дж. Температура нагревателя 100°С, температура холодильника 0°С. Найти: 1) КПД машины; 2) количество тепла, получаемого машиной за один цикл от нагревателя; 3) количество тепла, отдаваемого за один цикл холодильнику.

2.75. Идеальная тепловая машина, работающая по циклу Карно, получает за каждый цикл от нагревателя 2500 Дж. Температура нагревателя 400 К, температура холодильника

300 К. Найти работу, совершаемую машиной за один цикл, и количество тепла, отдавае-мого холодильнику за один цикл.

2.76. Идеальный газ, совершающий цикл Карно,70% количества теплоты, полученной от нагревателя, отдает холодильнику. Количество теплоты, получаемое от нагревателя, равно 5 кДж. Определить: 1) термический КПД цикла; 2) работу, совершенную при полном цик-ле.

2.77. Идеальный газ совершает цикл Карно. Газ получил от нагревателя количество теплоты 5,5 кДж и совершил работу 1,1 кДж. Определить: 1) термический КПД цикла;

2) отношение температур нагревателя и холодильника.

2.78. Идеальный газ совершает цикл Карно, термический КПД которого равен 0,4. Опре-делить работу изотермического сжатия газа, если работа изотермического расширения составляет 400 Дж.

2.79. Идеальный газ совершает цикл Карно. Температура нагревателя Т₁= 500 К, холо-дильника Т₂=300 К. Работа изотермического расширения газа составляет 2 кДж. Опре-делить: 1) термический КПД цикла; 2) количество теплоты, отданное газом холодильнику при изотермическом сжатии.

2.80. Многоатомный идеальный газ совершает цикл Карно, при этом в процессе адиабат-ного расширения объем газа увеличивается в n= 4 раза. Определитmтермический КПД цикла.

2.81. Идеальная тепловая машина работает по циклу Карно, при этом 80% тепла, полу-чаемого от нагревателя, передается холодильнику. Количество тепла, получаемого от нагревателя, равно 6,28 кДж. Найти:1) КПД цикла; 2) работу, совершенную при полном цикле.

2.82. КПД идеальной машины, работающей по циклу Карно, равен 0,25.Температура холодильника 7⁰С. Какова температура нагревателя? Как изменить температуру нагревателя, чтобы КПД увеличился в 2 раза?

2.83. Подсчитать работу, которую производит тепловая машина, работающая по циклу

Карно, за один цикл, если температура нагревателя 417°С, а холодильника 17 ⁰С и машина отдает холодильнику 400 Дж тепла.

2.84. Паровая машина мощностью в 14,7 кВт потребляет за 1 ч работы 8,1 кг угля с теплотворной способностью 3,3.10 ⁷Дж/кг. Температура котла 200⁰С.Температура холодильника 58⁰С. Найти фактический КПД машины() и сравнить с КПД ()

идеальной тепловой машины, работающей по циклу Карно, между теми же темпе-ратурами.

2.85. Найти изменение энтропии при переходе 8.10 ^-3кг кислорода от объема в 10 л при температуре 80⁰С к объему 40 л при температуре 300⁰С.

2.86. 6,6.10^-3кг водорода расширяются изобарически до удвоения объема. Найти изменение энтропии при этом расширении.

2.87. Найти изменение энтропии при изотермическом расширении 6.10 ^-3кг водорода от

I0 ⁵до 0,5. I0⁵Па.

2.88. 10,5.I0^-3кг азота изотермически расширяются от объемаV₁ =2.10^-3 м³до объема

V₂= 5.I0^-5м³. Найти изменение энтропии при атом процессе.

2.89. Во сколько раз необходимо увеличить объем v= 5 моль идеального газа при изотер-мическом расширении, если его энтропия увеличилась на 57,6 Дж/К?

2.90. При нагревании двухатомного идеального газа (v= 2 моль) его термодинамическая температура увеличилась вn= 2 раза. Определить изменение энтропии, если нагревание

происходит: 1)изохорно; 2)изобарно.

2.91. Идеальный газ (v= 2 моль) сначала изобарно нагрели, так что объем газа увеличил-ся вn₁= 2 раза, а затем изохорно охладили, так что давление его уменьшилось вn= 2 раза. Определить приращение энтропии в ходе указанных процессов.

2.92. Азот массой 28 г адиабатно расширили в n= 2 раза, а затем изобарно сжали до пер-воначального объема. Определить изменение энтропии газа в ходе указанных процесссов.

2.93. В сосуде емкостью 2,5.10 ^-3м³ находится 0,46 кг газа при температуре 27⁰С. Вычис-лить давление газа по уравнению Менделеева-Клапейрона и по уравнению Ва-дер-Ваальса, если для углекислого газаа= 3,03.10⁵Н м³/кмоль²ив= 0,043 м³/кмоль.

2.94. Кислород (v= 10 моль) находится в сосуде объемомV= 5 л. Определить: 1)внутрен-нее давление газа; 2) собственный объем молекул. Поправкиaиbпринять равными соот-ветственно 0,136 Н. м⁴/моль²и 3,17 .10^-5м³/моль.

2.95. Углекислый газ массой 6,6 кг при давлении 0,1 МПа занимает объем 3,75 м ³. Опре-делить температуру газа, если: 1) газ реальный; 2) газ идеальный. Поправкиaиbпринять равными соответственно 0,361 Н.м⁴/моль²и 4,28 .10^-5м³/моль.

2.96. Углекислый газ массой 2,2 кг находится при температуре 290 К в сосуде вмести-мостью 30 л. Определить давление газа, если: 1) газ реальный; 2) газ идеальный. Поправкиa иbпринять равными соответственно 0,361 Н. м⁴/моль²и 4,28.10^-5м³/моль

2.97. Плотность азота = 140 кг/м³, его давление Р = 10 МПа. Определить температуру газа, если: 1) газ реальный; 2) газ идеальный. Поправкиаиbпринять равными соответ-ственно 0,13 5 Н.м⁴/моль²и 3,86.10м³/моль.

2.98. Анализируя уравнение состояния реальных газов, определить значения поправок aиbдля азота. Критические давление и температура азота соответственно равны 3,39 МПа и 126 К.

2.99. В каких единицах СИ выражаются постоянные a и b, входящие в уравнение Ван-дер-Ваальса?

2.100. Анализируя уравнение состояния реальных газов, определить значения поправок aиbдля аргона. Критические давление и температура аргона соответственно равны 4,87 МПа и 151 К.

ПРИЛОЖЕНИЯ

Единицы тепловых величин

Наименование величин	Единица
	Определяющее уравнение	обозначение	Наименование и определение
Количество теплоты,внут- ренняя энер-гия		Дж	Джоульравен количеству теплоты ,экви- валентному работе 1 Дж
Тепловой по-ток (тепловая Мощность)		Вт	Ватт равен тепловому потоку, эквива- лентному механической мощности 1 Вт
Градиент температуры		К/м	Кельвин на метррамен температурному градиенту поля , в котором на участке длиной 1 м в направлении градиента температура изменяется на 1 К
Теплопровод-ность			Ватт на метр-кельвин рамен теплопро-водности вещества ,в котором при стационарном режиме с поверхностной плотностью потока 1 Вт/м 2устанавли-вается температурный градиент 1К/м
Теплоёмкость системы	С=	Дж/К	Джоуль на кельвинравен теплоёмкости системы , температура которой повы-шается на 1К при подведении к системе количества теплоты 1 Дж
Удельная теплоёмкость	С=		Джоуль на килограмм-кельвинрамен удельной теплоёмкости вещества, имеющего при массе 1 кг теплоёмкость 1 Дж/К
Молярная теплоёмкость	С m=		Джоуль на моль-кельвинравен молярной теплоёмкости вещества, имеющего при количестве вещества 1 моль теплоём-кость 1 Дж/К
Энтропия		Дж/К	Джоуль на кельвинравен изменению энтропии системы , которой при темпе-ратуре nК в изотермическом процессе сообщается количество теплотыnДж

Фундаментальные физические постоянные

Абсолютный 0 температурыt= - 273,15⁰C

Молярная газовая постоянная R=8,31 Дж/(моль.К)

Молярный объём идеального газа V₀ =22,41.10^-3м³/моль

при нормальных условиях

Нормальные условия:

атмосферное давление Р₀=101325 Н/м²

температура Т=273 К

Постоянная Авогадро N_A=6,022.10²³моль^-1

Постоянная Больцмана k=1,381.10^-23Дж/К