
- •Интегральное исчисление Лекция № 24. Тема 1: Неопределённый интеграл
- •1.1. Первообразная и неопределённый интеграл
- •1.2. Основные свойства неопределённого интеграла
- •1.3. Таблица неопределённых интегралов
- •1.4. Интегрирование методом замены переменной (способ подстановки)
- •Лекция № 25
- •1.5. Интегрирование некоторых функций, содержащих квадратный трёхчлен
- •1.6. Интегрирование по частям
- •1.7. Многочлены и рациональные дроби
- •Лекция № 26
- •1.8. Интегрирование рациональных дробей
- •1.9. Интегрирование тригонометрических функций
- •Лекция № 27
- •1.10. Интегрирование некоторых иррациональных функций
- •1.11. Понятие о неберущихся интегралах
Лекция № 25
1.5. Интегрирование некоторых функций, содержащих квадратный трёхчлен
Рассмотрим
интегралы вида
![]() .
Они с помощью замены
.
Они с помощью замены![]() приводятся к известным интегралам.
приводятся к известным интегралам.
Пример 1.
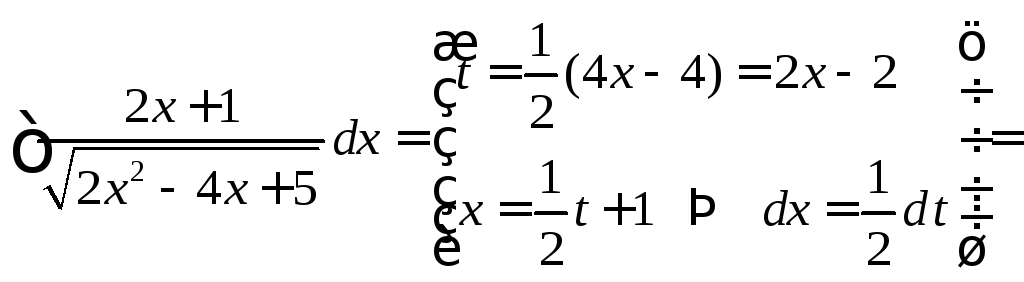
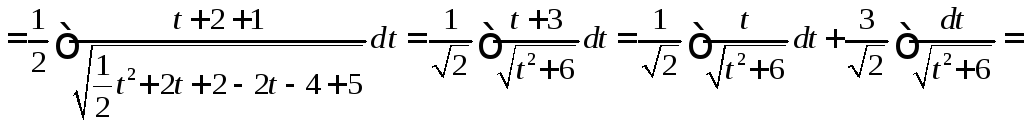

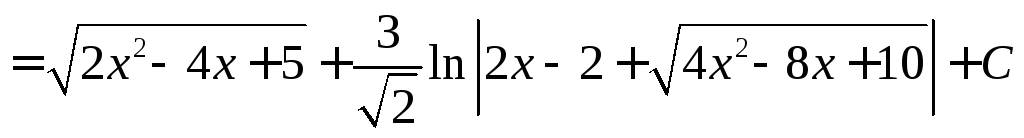 .
.
Замечание 1. Если для первого из рассмотренных интегралов квадрат-ный трёхчлен имеет действительные корни, то более целесообразно преобразовать подынтегральную функцию, представив её как сумму алгебраических дробей со знаменателями–множителями в разложении квадратного трёхчлена. Более подробно об этом будет рассмотрено в следующей лекции.
Пример 2.
Найти интеграл
![]() .
.
Преобразуем подынтегральную функцию:
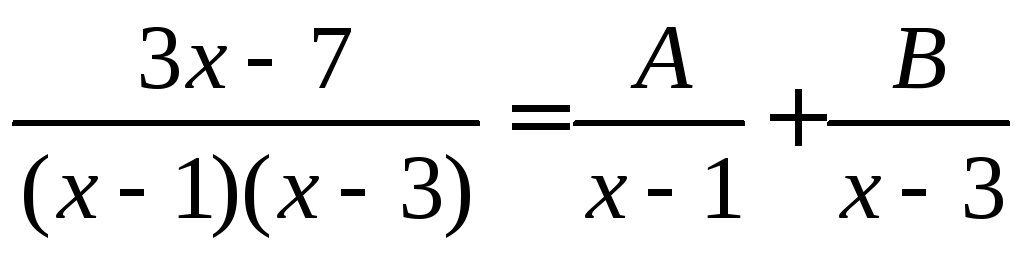 .
.
Определим коэффициенты А и В, выполнив сложение дробей и приравняв числители дробей правой и левой частей равенства:
![]() .
.
Приравнивая коэффициенты при х и свободные члены, получим
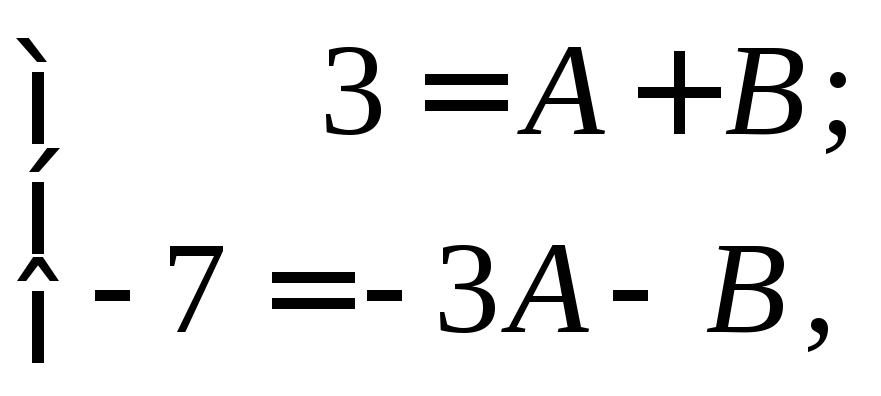
откуда
![]() .
.
Тогда имеем
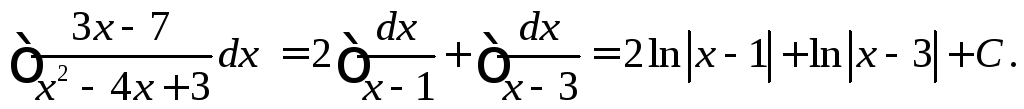
1.6. Интегрирование по частям
Пусть u и v дифференцируемые функции. Тогда справедлива формула
![]() .
(1)
.
(1)
Проинтегрировав выражение (1), получаем формулу интегрирования по частям
![]() .
(2)
.
(2)
Формула (2) применяется при нахождении интегралов от функций вида:
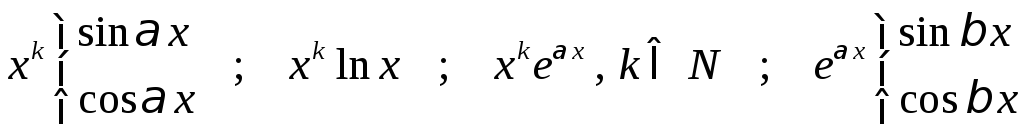
и некоторых других.
Пример 3.
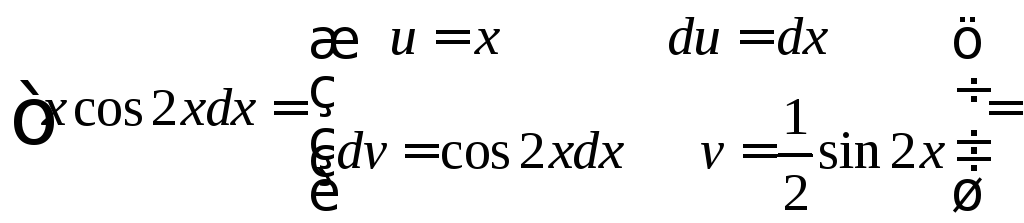
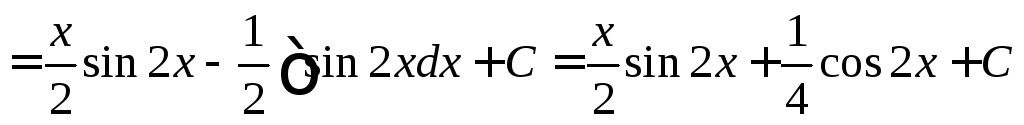 .
.
Пример 4.
Найти интеграл
![]() .
Воспользуемся формулой (2) дважды.
.
Воспользуемся формулой (2) дважды.
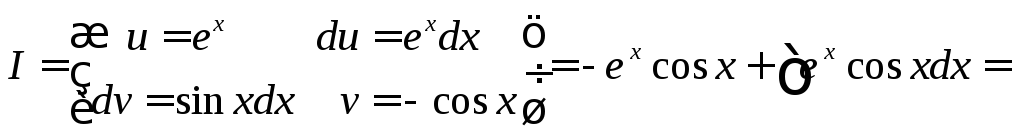
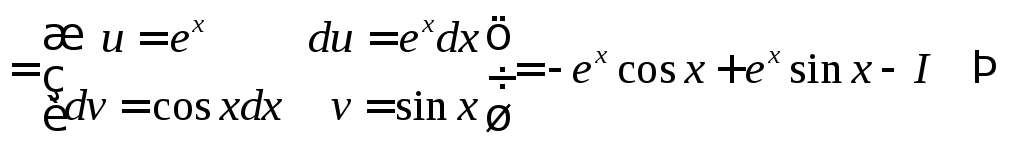

1.7. Многочлены и рациональные дроби
Вначале напомним некоторые положения из алгебры.
Рассмотрим многочлен
п-ой
степени
![]() с действительными коэффициентами. Если
с действительными коэффициентами. Если![]() ,
то
,
то![]() называется корнем многочлена. Согласно
основной теоремы алгебры любой такой
многочлен можно представить в виде
называется корнем многочлена. Согласно
основной теоремы алгебры любой такой
многочлен можно представить в виде
![]() (3)
(3)
где
![]() действительные корни кратности
действительные корни кратности![]() ,
квадратичные множители в формуле (3)
действительных корней не имеют и
,
квадратичные множители в формуле (3)
действительных корней не имеют и![]() .
.
Пример 5.
Представить в виде (3) многочлен
![]() .
.
![]()
![]()
Здесь
![]() и
и![]() .
.
Определение 1. Рациональной функцией или дробью называется функция вида
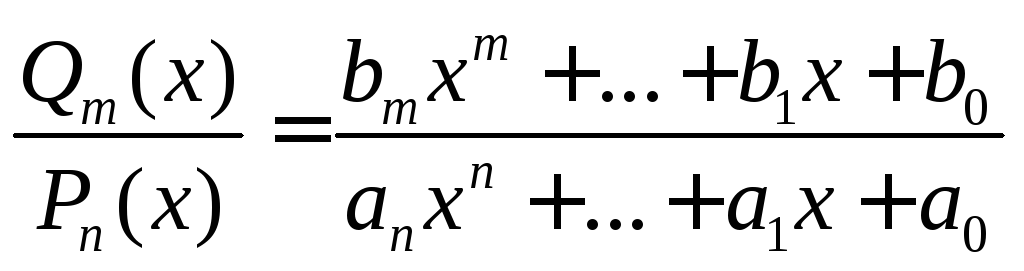 .
(4)
.
(4)
При этом будем
считать, что
![]() (это всегда можно сделать путём деления
числителя и знаменателя на
(это всегда можно сделать путём деления
числителя и знаменателя на![]() )
и
)
и![]() .
Такая рациональная дробь называется
правильной
рациональной дробью.
.
Такая рациональная дробь называется
правильной
рациональной дробью.
В противном случае, нужно выделить целую часть, разделив числитель на знаменатель, т.е. представить дробь в виде
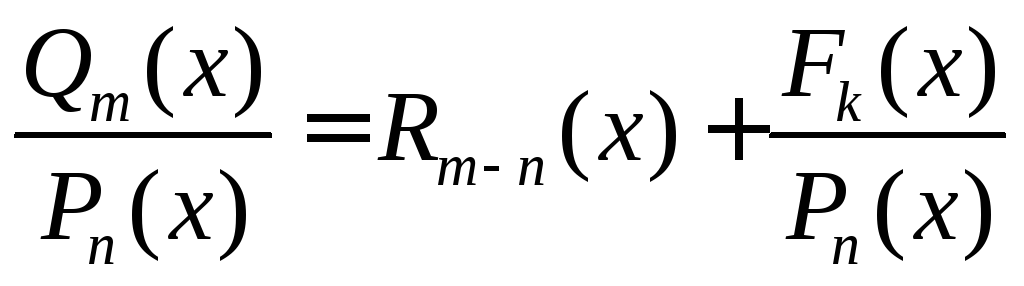 ,
,
где
![]()
многочлен степени
многочлен степени
![]() ,
а
,
а![]()
многочлен степени меньше
многочлен степени меньше
![]() .
.
Пример 6. Выделить целую часть неправильной рациональной дроби
![]() .
.
Выполним деление
многочленов
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, дробь можно представить в виде
 .
.
Определение 2. Рациональные дроби вида
1.
![]() ;2.
;2.
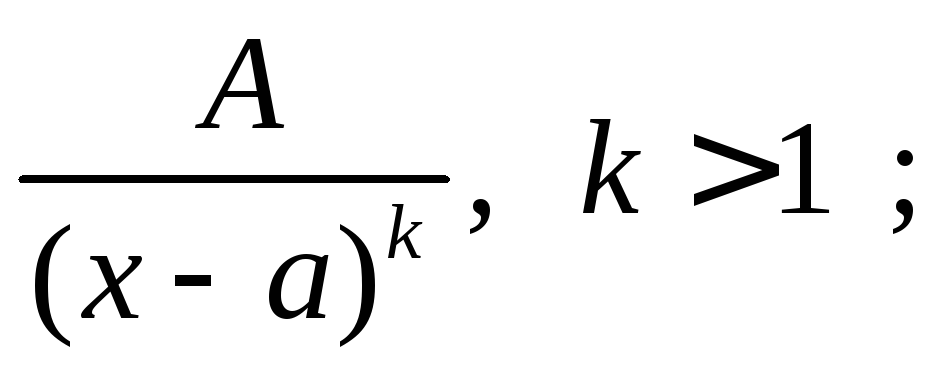 3.
3.
![]() 4.
4.
![]()
называются простейшими дробями.
Интегралы от дробей
1-2
являются табличными. Интеграл от дроби
3
был уже рассмотрен в пункте 1.5. Интеграл
от последней дроби путём замены
![]() приводится к известному интегралу и
интегралу вида
приводится к известному интегралу и
интегралу вида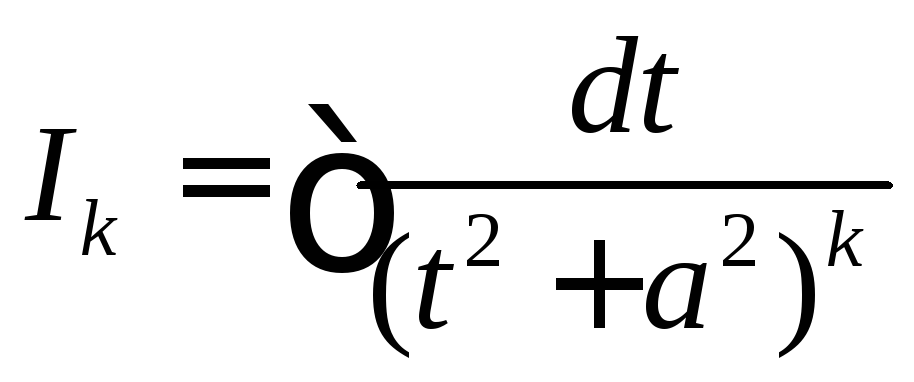 ,
для вычисления которого с помощью
формулы интегри-рования по частям
можно получить рекуррентную формулу
,
для вычисления которого с помощью
формулы интегри-рования по частям
можно получить рекуррентную формулу
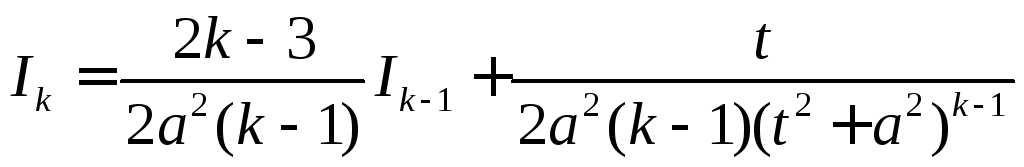 .
.
Например, если
![]() ,
то имеем
,
то имеем
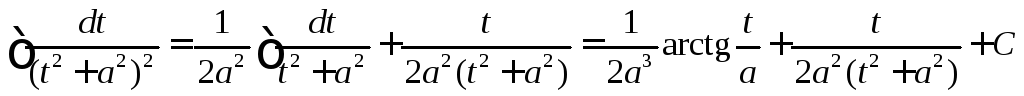 .
.
Таким образом, нахождение интегралов от простейших дробей не представляет принципиальных трудностей.
В алгебре доказывается следующая теорема.
Теорема. Если в правильной рациональной дроби знаменатель можно представить разложением (3), то её можно разложить на сумму простейших дробей, т.е.
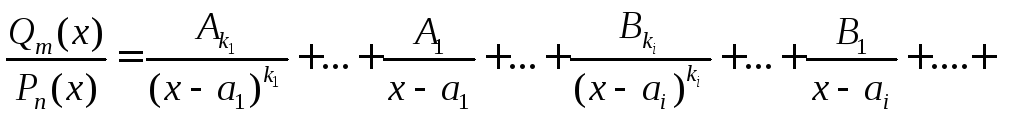
 .
.
С использованием этой теоремы преобразуется подынтегральная рациональная функция и нахождение интеграла приводится к интегрированию простейших дробей. Коэффициенты в числителях этих дробей вычисляются методом неопределённых коэффициентов.
Пример 7. Для выражения, полученного в примере 6, имеем
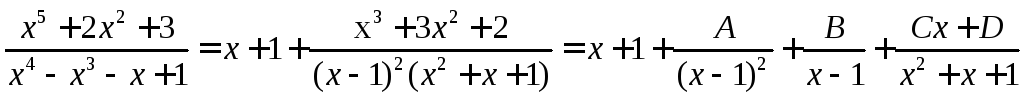 .
.
Коэффициенты
![]() определим методом неопределённых
коэф-фициентов.
Выполним сложение дробей и приравняем
числители правильной дроби
в левой части
и результата сложения дробей (числителя)
в правой части
определим методом неопределённых
коэф-фициентов.
Выполним сложение дробей и приравняем
числители правильной дроби
в левой части
и результата сложения дробей (числителя)
в правой части
![]() .
.
Приравняв коэффициенты при одинаковых степенях х, получаем систему линейных уравнений
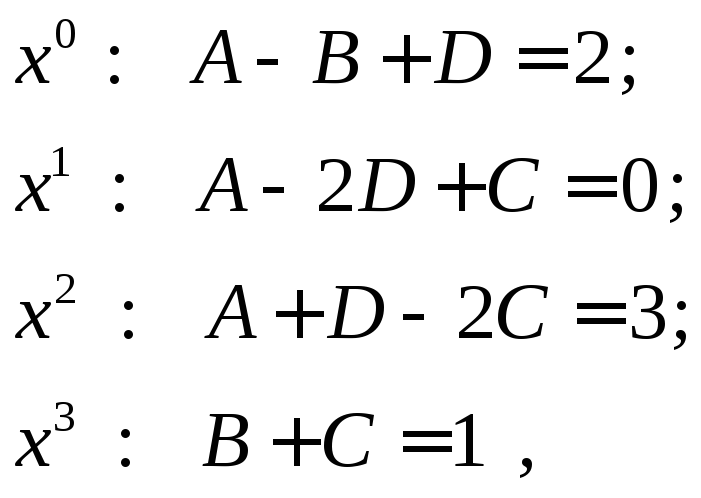
из которой следует
![]() .
Окончательно получим
.
Окончательно получим
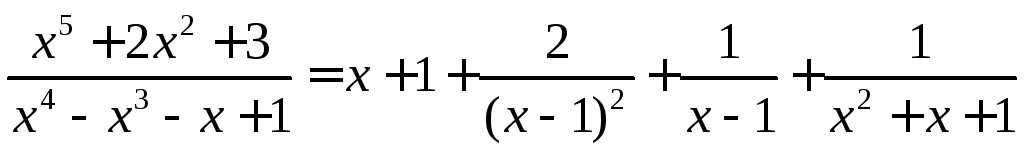 .
.
