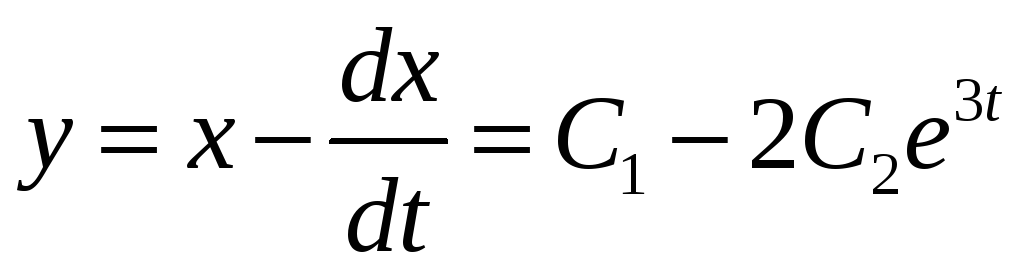6.2. Решение нормальных систем ду методом исключений
Решение системы
(2) сводится к решению ДУ-п
методом исключений.
Продифференцируем
по х
первое уравнение системы (2)
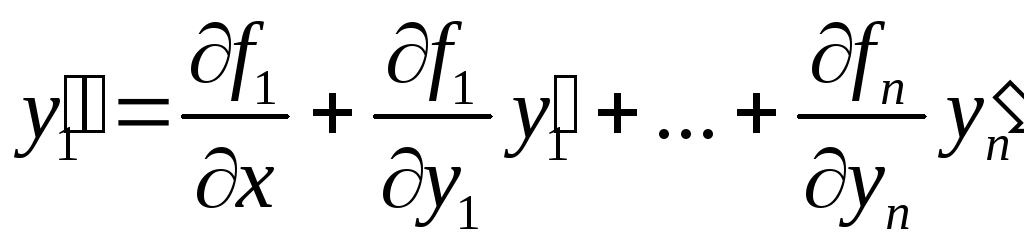 .
.
С учетом остальных
уравнений системы это выражение
примет вид
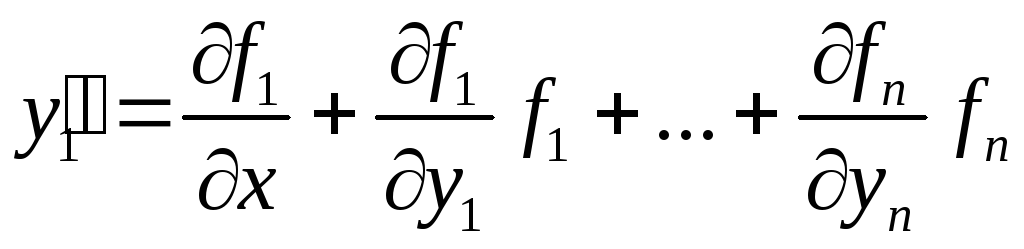 или
или
 .
.
Аналогично, ещё
раз продифференцировав, получаем

и т. д., пока не
найдём п-ю
производную

Таким образом,
получаем систему п
уравнений
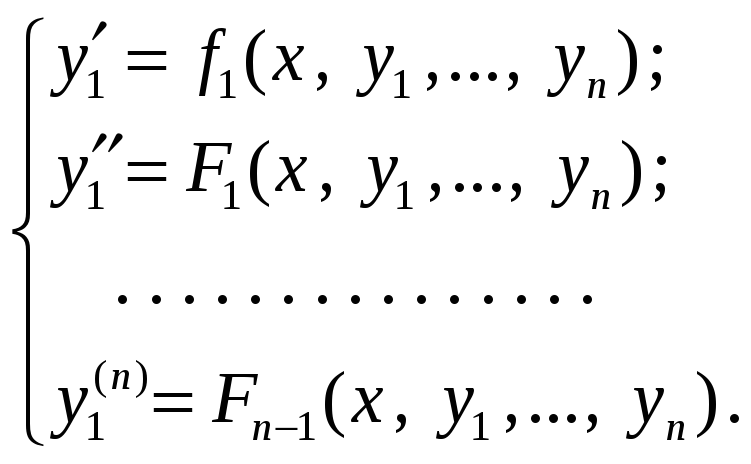 (4)
(4)
Из первых п
1
уравнений системы (4) выразим
 через переменные
через переменные
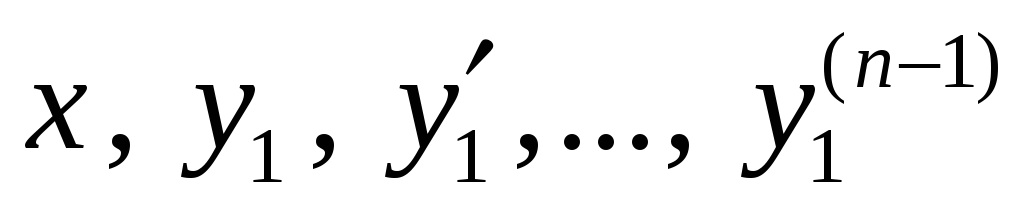 .
Подставляя их значения в последнее
урав-нение системы (4), имеем
.
Подставляя их значения в последнее
урав-нение системы (4), имеем
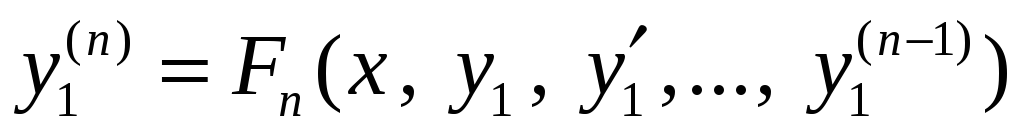 .
(5)
.
(5)
Решая уравнение
(5), находим
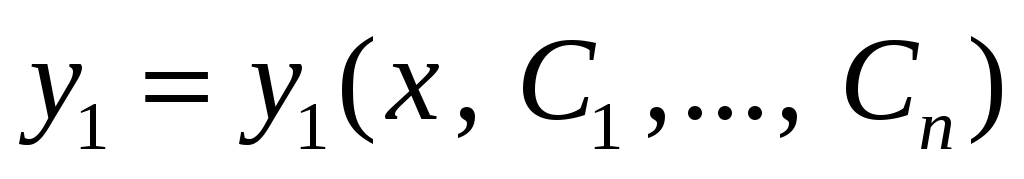 ,
а с помощью выражений для
,
а с помощью выражений для
 определяем и эти функции.
определяем и эти функции.
Замечание 1.
Из приведённых выше рассуждений видна
структура общего решения системы ДУ
(2).
Замечание 2.
Часто систему уравнений можно сразу
сводить к уравнению (5), минуя систему
(4). В частности, это относится к линейным
системам ДУ.
Пример 2.
Найти общее решение системы
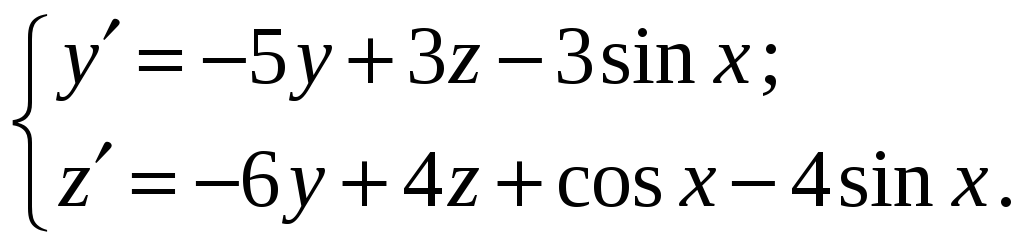
Из первого
уравнения найдем

и подставим во
второе уравнение
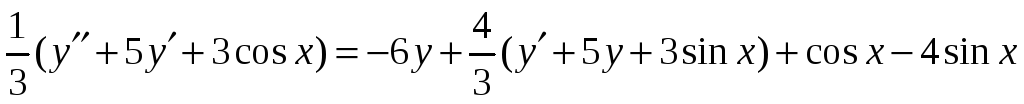 .
.
Умножим на 3
и приведём подобные члены
 .
.
Составим
характеристическое уравнение
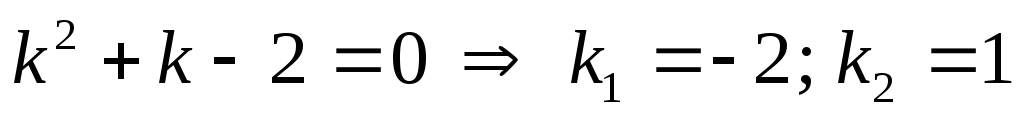 .
.
Имеем
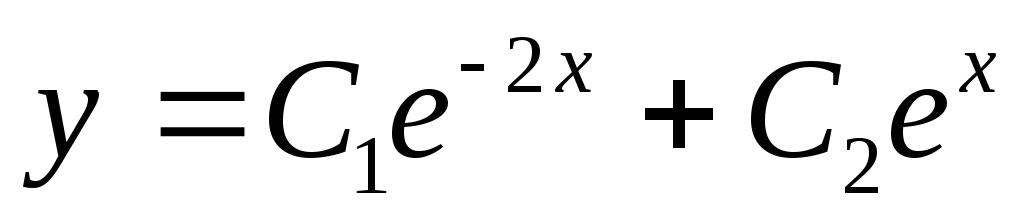 .
.
Тогда, с учетом
выражения для z,
получаем
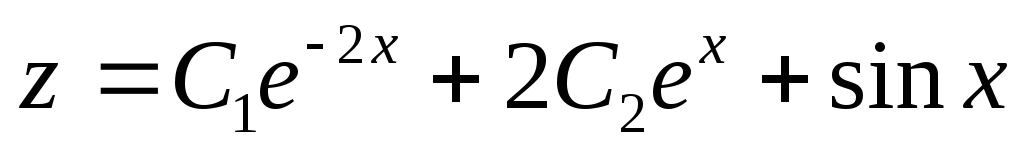 .
.
Пример 3.
Решить задачу Коши
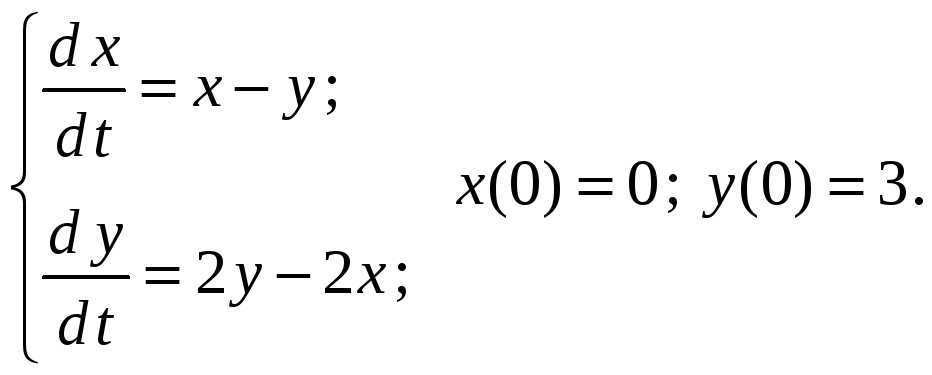
Из первого
уравнения находим

и подставляем во
второе уравнение

Составим
характеристическое уравнение
 .
.
Тогда
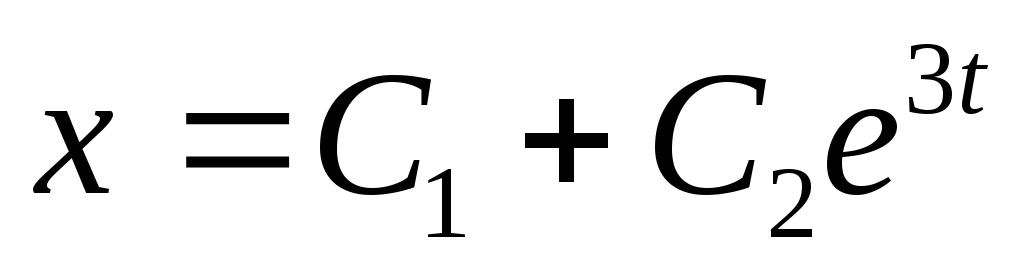
и
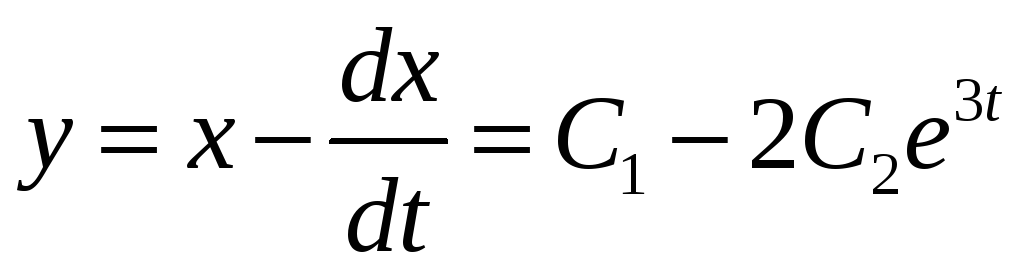
Из начальных
условий получаем систему для нахождения
 и
и

Окончательно
имеем
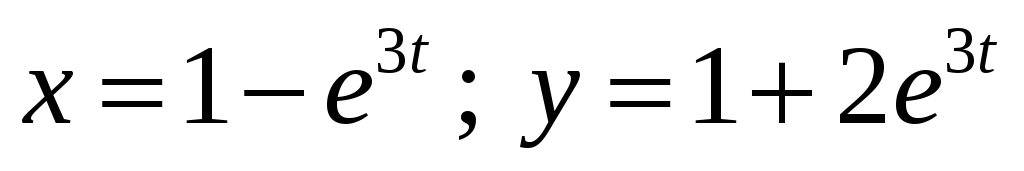 .
.


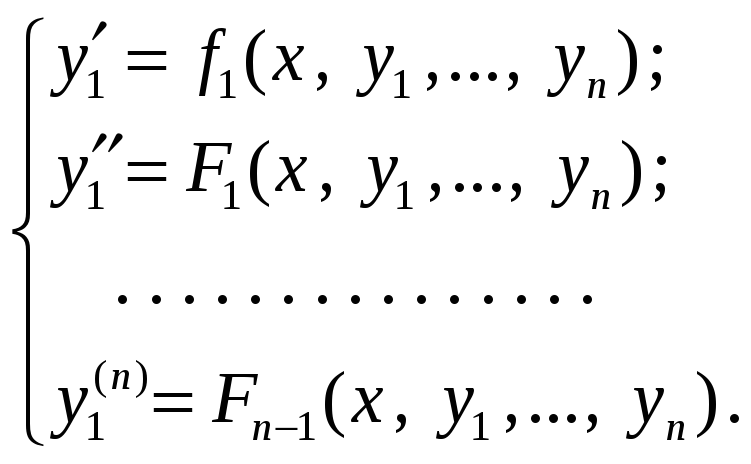 (4)
(4)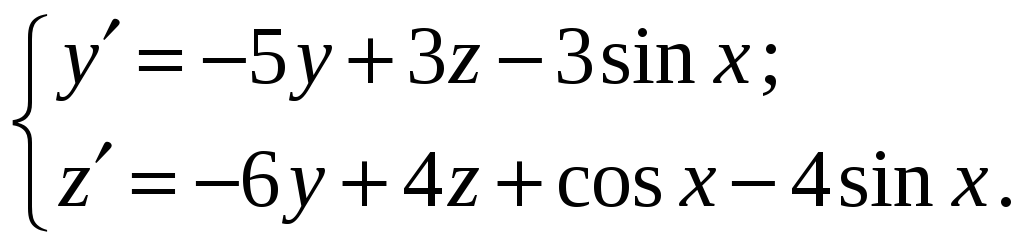

 .
.