
- •Логические операции
- •Логические функции.
- •Функцией алгебры логики
- •Элементарные функции алгебры логики
- •Свойства конъюнкции, дизъюнкции и отрицания
- •Пример 3:
- •Свойства функций сложения по модулю 2, импликации, штриха Шеффера и стрелки Пирса (функции Вебба)
- •Основные классы фал
- •Известно, что любая булева функция, отличная от нуля, может быть представлена совершенной днф.
- •2. Операции поглощения, которая состоит в замене выражения на,
- •Минимальные формы
- •Многомерный куб
- •Карты Карно
- •Карты Карно для 4-х переменных.
- •Понятие двоичного сигнала. Способы его кодирования.
- •Понятие логической системы. Типы логических систем.
- •Задачи анализа и синтеза комбинационных схем.
- •Построение комбинационных схем (кс) по минимальным нормальным формам в различных базисах.
- •Задача факторизации (факторного преобразования) булевой функции.
- •Построение одновыходных схем. Декомпозиция булевых функций.
Функцией алгебры логики
ФАЛ называется функция, дающая однозначное отображение Х в Y.
Число различных
ФАЛ, зависящих от n аргументов, конечно
и равно
![]() .
.
-
x1, x2, …, xn-1, xn
f (x1, x2, …, xn-1, xn)
0 0 … 0 0
α1
0 0 … 0 1
α2
… … … … …
… … …… … … …
1 1 … 1 0
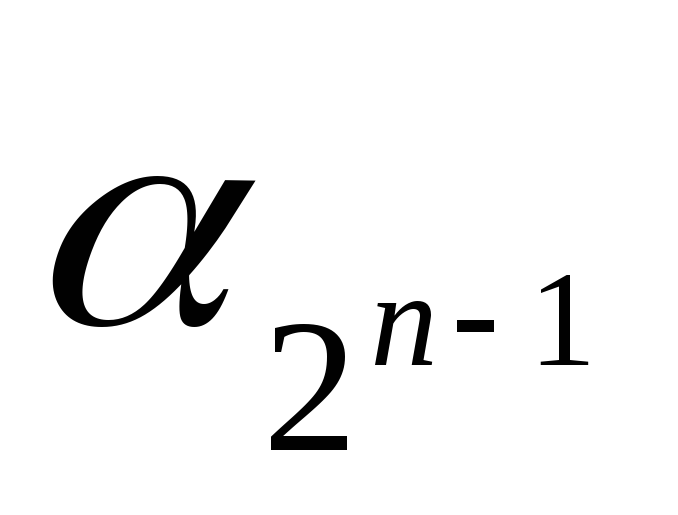
1 1 … 1 1
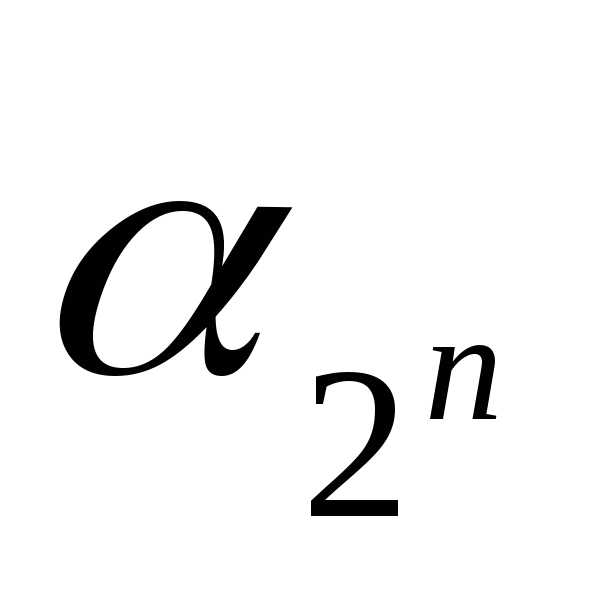
Формы задания Булевой функции:
1. Аналитическая (в виде логического выражения)
2. Табличная (в виде таблицы истинности)
3. Геометрическая
4. Таблично-графическая (в виде карты Карно)
5. Числовая
6. Символическая форма
1) Аналитическая:
![]()
2) Табличная:
![]()
|
x1 |
x2 |
x3 |
|
y |
|
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
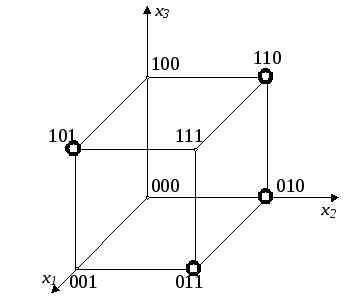
Если наборам
значений аргументов ФАЛ сопоставляет
точки n- мерного пространства, то множество
![]() наборов
определяет множество вершин n- мерного
единичного куба. Таким образом, областью
определения ФАЛ, зависящей от n аргументов,
является множество вершин такого куба.
наборов
определяет множество вершин n- мерного
единичного куба. Таким образом, областью
определения ФАЛ, зависящей от n аргументов,
является множество вершин такого куба.
Пример.
ФАЛ f(x1, x2, x3) может быть задана геометрически .
f(101, 110, 010, 011)=1
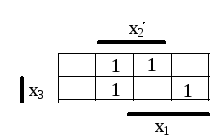
Или на картах Карно или на картах Вейча

Значения ФАЛ могут быть заданы не на всех возможных наборах аргументов. На некоторых значения функции могут быть не определены. Такие функции называют не полностью определенными.
Элементарные функции алгебры логики
Рассмотрим множество
элементарных ФАЛ. Начнем со случая,
когда длина слова n=0. По формуле,
определяющей число функций логики,
вычисляем, что при n=0
![]() =
2.
=
2.
f1=0; f2=1.
Эти две функции совпадают с константами.
В случае n=1 мы имеем две функции, существенно зависящие от аргумента x, эти две функции определяются таблицей
-
x1
f 3
f 4
0
0
1
1
1
0
Эти две функции также относят к элементарным, и они записываются следующим образом
f 3=x;f 4=![]() (читается
«неx»).
(читается
«неx»).
Функцию f 4 называют функцией отрицания.
В случае n=2 имеем десять различных функций, существенно зависящих отаргументовx1 иx2.
|
|
|
x1 x2 |
x1& x2 |
x1 ~ x2 |
x1x2 |
x1 x2 |
x1/x2 |
x1 |
|
x 1 |
x 2 |
f 5 |
f 6 |
f 7 |
f 8 |
f 9 |
f 10 |
f 11 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
Функция f5(x1,x2) =x1x2(дизъюнкция).
Функция f6(x1,x2) =x1&x2(конъюнкция).
Вместо символов & часто применяют символ умножения «•» или вообще опускают также, как и в обычной алгебре.
Функция f7носит название функции эквивалентности или функции равнозначности
f7(x1,x2) = x1~x2
иf7(x1,x2) =x1x2.
Функция f8носит название импликацииx1вx2. Она обозначаетсяf8(x1,x2) =x1x2.
Функция f9 носит название функции Вебба (или ее называют еще стрелкой Пирса) и обозначается
f 9(x1,x2) = x1vx2.
Функция f9называется функцией (штрихом) Шеффера и обозначается следующим образомf 10(x1,x2) =x1 x2.
Функция f 11обычно называется функцией сложения по модулю2.
f
11(x1,x2)
= x1![]() x2.
x2.
Рассмотрение одиннадцати функций позволяют строить новые функции двумя основными способами:
путем перенумерации аргументов;
путем подстановки в функцию новых функций вместо аргументов.
Функцию, полученную из функций f 1, f 2, f 3, …, f k путем применения этих правил будем называть суперпозицией функцииf 1, f 2, f 3, …, f k.
Имея, например, элементарные функции отрицания, дизъюнкции, эквивалентности и импликации, можно составить следующие новые функции ФАЛ.
Используя таблицы, определяющие элементарные функции, можно задать любую функцию ФАЛ, являющуюся суперпозицией этих функций.
Пример. Пусть требуется представить в виде таблицы следующую функцию
f (x1,x2,x3)={[(![]() ~x2)
(x1
x2)] (x1
~x2)
(x1
x2)] (x1![]() x2)}x3.
x2)}x3.
Будем строить ФАЛ последовательно.
|
x1 |
x2 |
x3 |
|
|
x1x2 |
[ ] |
x1x2 |
{ } |
f (x1,x2,x3) |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
ВЫРАЖЕНИЕ ОДНИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ ЧЕРЕЗ ДРУГИЕ
Функция f 8(x1,x2) =x1x2(импликацияx1вx2) может быть записана посредством функций дизъюнкции и отрицания
x1>x2=![]() x
2.
x
2.
Доказательство осуществляется посредством таблиц истинности.
|
x
1 x
2 x1x2 0 0 1 0 1 1 1 0 0 1 1 1 |
x1 x2 0 0 1 1 0 1 1 1 1 0 1 0 1 1 1 1 |
Функцию эквивалентности f7(x1,x2)=x1~x2 =x1x2выразим посредством других функцийx1~x2= (
 x2)&(x
1
x2)&(x
1
 )
)
|
x 1 |
x 2 |
x1~x2 |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
|
x 1 |
x 2 |
|
|
|
x1 |
( |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
f 11(x1,x2) = x1
 x2=
x2=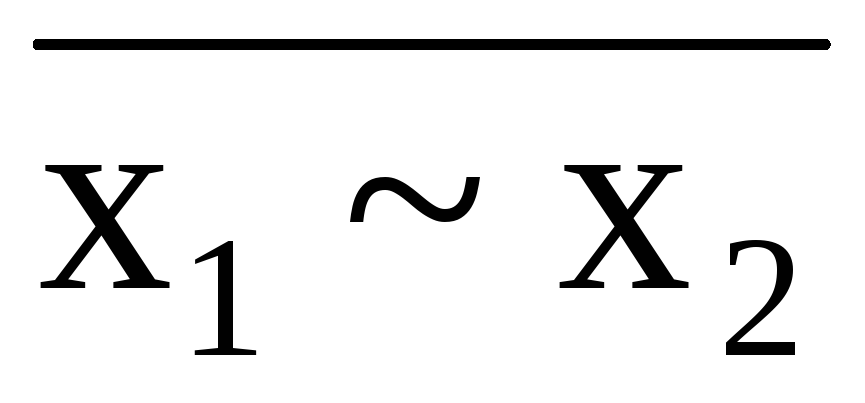
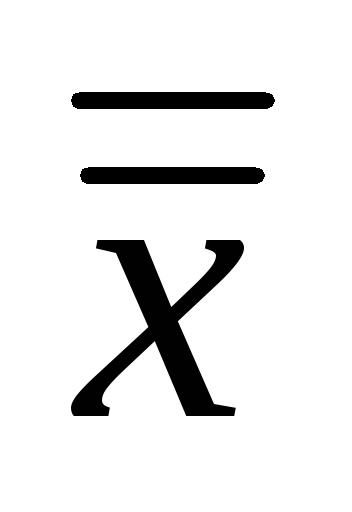 = x
= x
|
x |
|
|
|
0 |
1 |
0 |
|
1 |
0 |
1 |
x1& x2=
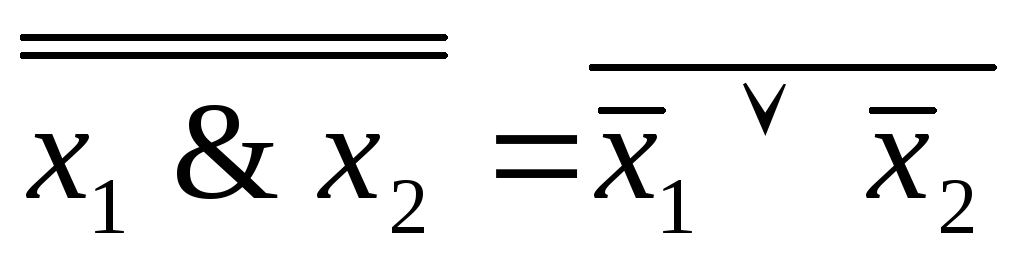
6. x1![]() x2=
x2=![]()
