Лекция 1 _Комплексные числа / Комплексные числа

23

Введение

(это введение является дополнением к введению из папки 1.1.0_...)

Математические методы исследования всегда играли и играют огромную роль в «природоведческой науке». Сами эти методы непрерывно развиваются и находят новые области своего применения. А новые и новейшие их приложения зачастую требуют либо усовершенствования самих методов исследования, либо даже развития новых направлений математики.

Математика – это точная наука, изучающая изначально «количественные соотношения и пространственные формы реального (окружающего нас) мира». Для применения ее методов исследования необходима формулировка системы аксиом, обобщающей основные закономерности конкретной исследуемой области в форме математической модели. Последующие строгие логичные рассуждения позволяют устанавливать следствия из этих аксиом. Естественно, что полученные в результате новые знания о свойствах этой математической модели тоже формулируются в строгой логической форме.

Математика – это абстрактная наука. Системы аксиом формируют логические модели, которые затем и являются объектами изучения. Сами модели строятся вначале для описания и исследования того или иного конкретного (наблюдаемого) явления. Но в силу своей абстрактности часто оказывается, что одна и та же математическая (логическая) модель может описывать математические свойства, то есть количественные соотношения, присущие очень далеким друг от друга и по своему содержанию, и даже по предметной области реальным процессам. Например, решением квадратного уравнения является и время свободного падения тела с высоты , и, возможно, значение =Р(А) - вероятности появления наблюдаемого события в отдельном испытании, если для независимых испытаний значение дисперсии, например, биномиального распределения, σ² = , где , известно. В этом проявляется сила математики, универсальность и общность её методов.

Для математики важна не природа объектов рассматриваемой «логической модели», а определенные «соотношения», существующие между ними.

С появлением быстродействующих вычислительных машин произошел большой качественный скачок в использовании математических методов исследования. Математика стала завоевывать те области знания, где совсем недавно применялась мало, либо ее применение даже не представлялось возможным: медицина, экология, экономика, лингвистика, социология и т. д.

Поэтому современный инженер должен хорошо владеть и классическими, и современными, связанными с расчётами на ЭВМ, математическими методами исследования, которые применимы в его предметной области. Ему обязательно необходимо знать границы и условия применимости известной или новой математической модели, либо уметь их определять.

При решении конкретной задачи правильный выбор модели и методов решения уравнений, получаемых для нее – это залог успеха. Более того, часто, это залог того, что в результате будет получено больше полезной информации об изучаемом предмете (явлении), чем можно было заранее предвидеть. Формулы могут оказаться «умнее» применяющего их!... Это связано с тем, что математический аппарат таит в себе много скрытой информации: «богатств, накопленных в течение веков».

Свободное владение математическими методами приобретается, накапливается и развивается в процессе систематических занятий, длительной и настойчивой работы. Тому, кто последовательно приобретает «твердые» и точные знания математических фактов, легче и проще двигаться дальше. Усвоив одно, он усваивает и последующее. Для успешного обучения важно выучить (!) основные математические понятия: определения, аксиомы, точные формулировки лемм и теорем. Составление о них лишь приближенного, расплывчатого представления только вредит обучению (!). Неточные знания не позволяют понять взаимосвязи между условием и решением, между аксиомами и следствиями из них, дающими новые знания.

Развитие умения логически мыслить при планомерном овладении математическим аппаратом, включающем изучение доказательств лемм и теорем, поиск ответов на дополнительные вопросы и решение контрольных заданий, позволяют правильно использовать математические методы, что даёт «большую экономию мышления».

§ 1. Числа натуральные, целые, рациональные и иррациональные.

Знакомство с количественными соотношениями начинается с прямого счета: 1, 2, 3, 4, 5, … . Им пользуются при определении количества однородных предметов: тетрадей, книг, CD дисков и т. д. Результат достигается сложением положительных целых чисел. Например, следующее за числом число получается прибавлением единицы к . Все такие числа образуют совокупность (множество) натуральных чисел, которое обозначается заглавной буквой латинского алфавита:

(1)

В фигурных скобках указаны элементы этого множества.

Определение–пояснение: множеством называют совокупность однородных элементов, объединенных общим свойством или признаком.

Обратный счет встречается при решении задач связанных с вычитанием из одного натурального числа второго. Например, вычитая из числа единицу, получим число . Вычитая единицу раз, подряд, из числа , получим число «0», обозначающее отсутствие перечисляемых предметов, их количество равно нулю. Дальнейшее вычитание приводит к отрицательным числам: , ≡ и т. д. Вычитание обратно сложению. Так равенству отвечает число , получаемое вычитанием большего числа 5 из меньшего числа 3. Натуральные числа, число «0» и отрицательные целые числа образуют множество целых чисел. Это множество обозначают заглавной буквой латинского алфавита:

(2)

Арифметическая операция «умножение» является сокращенной записью сложения одинаковых чисел. Так запись , не зависящая от порядка множителей, обозначает равные количества, получаемые сложением или четырех чисел 3, или трех чисел 4: .

Операция «деление» появляется, как операция обратная умножению. Уравнение обращается в тождество для значения . Но не всегда уравнение , где и , имеет решением число . Когда не делится без остатка на , получаем нецелое число

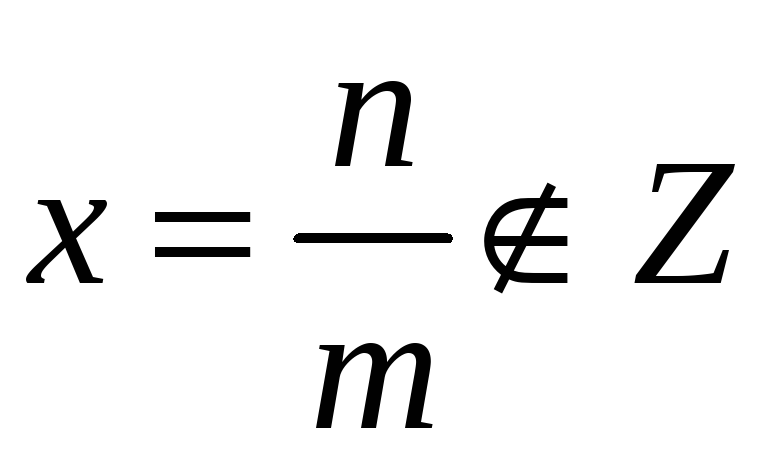(3)

“Довиетовские” алгебраисты ограничивались заявлением, что «такое деление не возможно». Сейчас это рациональные числа.

Несократимые (положительные и отрицательные) дроби , где , , дают множество рациональных чисел, которое обозначают заглавной буквой латинского алфавита, 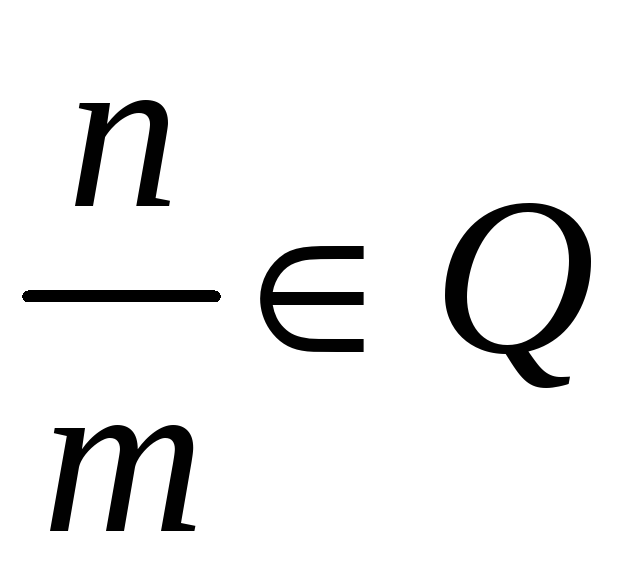. Все рациональные числа представляются периодическими десятичными дробями. Так, 2/3=0,66666…= 0,(6).

Степень числа – это сокращённая запись умножения нескольких одинаковых чисел. Так, при определении, например, общей длины приставленных друг к другу трех одинаковых стержней, по 3см каждый, мы получим . Для математики не существенны единицы измерения складываемых однородных величин, то есть величин одинаковой размерности. Важны только количественные соотношения. Тогда в нашем случае , и говорят: «три в степени 2 равно 9». В общем случае произведение одинаковых чисел «» записывают сокращенно, как «» в степени , то есть , где «» – основание и – степень.

Для операции «возведение в степень» обратной будет операция «извлечение корня». Так, для извлечённым корнем будет: . Говорят: «корень -ой степени из числа ». Операция «извлечение корня» записывает решение уравнение . Замечание: когда – четное число, тогда , так как проверка даёт .

В отличие от уравнения с решениями , для которых , решениями уравнения являются числа . Они уже не принадлежат ни множеству целых, ни множеству рациональных чисел, . Знак «» обозначает объединение множеств и . Такие числа, как: , ,… число «», число «» и др. представляются бесконечными непериодическими дробями. Их объединяют в множество иррациональных чисел, обозначаемое заглавной буквой латинского алфавита.

Иррациональное число появляются, например, когда несколько отрезков «несоизмеримы». Для них нельзя найти отрезок конечной длины, укладывающийся целое число раз в каждом из измеряемых отрезков. Так, иррациональность числа связана с несоизмеримостью катетов равнобедренного прямоугольного треугольника с его гипотенузой; – иррациональное число, так как ребра куба несоизмеримы с его объемной диагональю; число – иррациональное число вследствие несоизмеримости длины окружности с ее диаметром. Число тоже иррациональное число, так как оно по определению равно бесконечной сумме убывающих рациональных чисел:

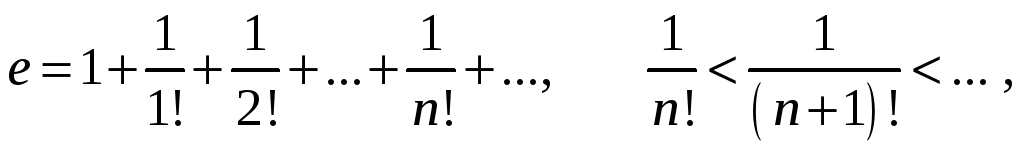, (4)

где , читают «число эн факториал». «Эн факториал» равен произведению всех натуральных чисел от 1 до . По определению 0! ≡ 1.

Объединённая совокупность целых, рациональных и иррациональных чисел образуют множество действительных чисел. Его обозначают заглавной буквой латинского алфавита:

. (5)

Важно, что действительные числа «сплошь» заполняют числовую ось. То есть между любыми двумя сколь угодно близкими числами можно вставить бесконечное число действительных чисел. Аналогичным свойством обладают и рациональные числа: «между двумя не равными рациональными числами всегда можно вставить тоже рациональное число». Это свойство действительных (и рациональных) чисел играет «важную» роль в теории пределов, изучаемой в первом семестре. Но вычисления на ЭВМ нарушают это свойство действительных чисел. Дело в том, что машинное представление числа с конечной мантиссой и порядком всегда содержит только конечное число чисел. А множества чисел, которыми мы обычно пользуемся, бесконечные. Это может привести к ошибочному результату при решении на ЭВМ и нелинейных уравнений, и систем линейных уравнений, и дифференциальных уравнений. Об этом, по крайней мере, нужно знать. Поэтому, по возможности, нужно проверять полученное на ЭВМ решение на «здравый смысл», а в определенных, частных, случаях проверять его совпадение с уже имеющимися очевидными и проверенными результатами.

Стоит отметить, что расширение числового «множества» от натуральных чисел до действительных чисел не является произвольным. В общем, ожидаемое появление «более сложных» множеств чисел при включении в рассмотрение новых типов задач и новых уравнений, например, степенных, показательных и т. д., оказывается, также должно быть закономерным…

«В природе» имеется некий механизм (схема) расширения числового множества (числового поля). Фундаментальная идея, дающая такую общую схему, сформулирована немецким математиком Германом Хенкелем в 1867 г. Её элементы ранее рассматривал Уильям Гамильтон. Её называют «принципом перманентности». Согласно этой схеме:

1. Среди элементов расширенного числового множества содержится последовательность натуральных чисел.

2. Есть критерий, устанавливающий равенство или неравенство всех элементов числового множества, а в случае, когда элементы являются натуральными числами, этот критерий превращается в известное правило сравнения натуральных чисел.

3. Для любых двух элементов множества задаётся схема сложения и умножения, подчиняющаяся перестановочному, сочетательному и распределительному законам. Она обязательно превращается в схему действия над натуральными числами, когда элементы множества являются таковыми.

§ 2. Комплексные числа.

Дальнейшее расширение числового «множества» связано с рассмотрением задач, которые на множестве действительных чисел не имеют решения. Например, уже простейшее квадратное уравнение

, (6)

не имеет решения на множестве действительных чисел. Ясно, что квадрат любого действительного числа не может быть числом отрицательным. В сум­ме с положительным числом 1 оно дает число большее нуля, ? Выход заключается в том, чтобы в формальном решение уравнения (6) считать, по определению, новыми числами – «мнимой единицей». Обозначают это число буквой и связывают с решением со знаком « +»: . Тогда естественно вторым корнем будет . Это позже будет подтверждено общей формулой для корней из произвольного числа.

Тогда, согласно (6), основное свойство числа :

. (7)

Решением аналогичного уравнения теперь будет . Проверку результата даёт тождество: .

Определение функции , где читают «модуль числа »:

Модуль любого действительного числа, , всегда имеет неотрицательное значение, получаемое согласно следующему «предписанию»:

. (8)

Усложним задачу. Решим теперь квадратное уравнение

, (9)

Для любых . Известно, что оно имеет действительное решение

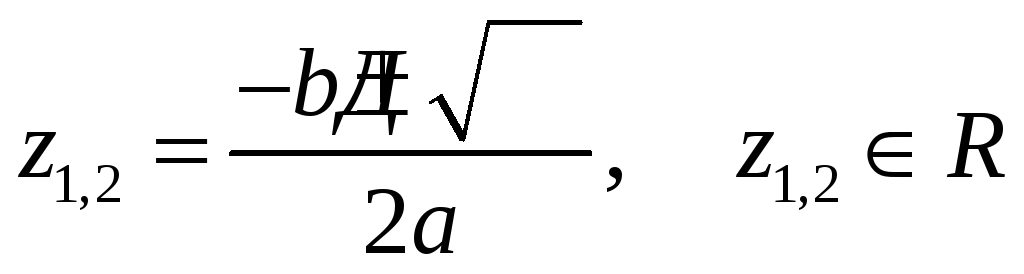, (10)

если дискриминант уравнения , и такого решения нет, если . Но применение в таком случае мнимой единицы со свойством (7) позволяет явно записать и получить явные решения уравнения (9) в виде двух новых, комплексных, чисел с мнимой единицей:

; (10´)

В комплексных числах и обозначают их действительную часть, записывая также: . Далее, – мнимая часть числа и – мнимая часть числа , записывая также: . Числа и в (10´) вещественные, и .

Числа и называют комплексно сопряженными. Обозначают комплексное сопряжение или «*» справа вверху от числа, или чертой над ним

, . (11)

Операция комплексного сопряжения меняет только знак мнимой части комплексного числа z на противоположный знак (см. равенства (10´)).

Каждую формулу (10´) надо считать, как единую запись комплексного числа в координатной форме. Это одно число, состоящее из двух частей:

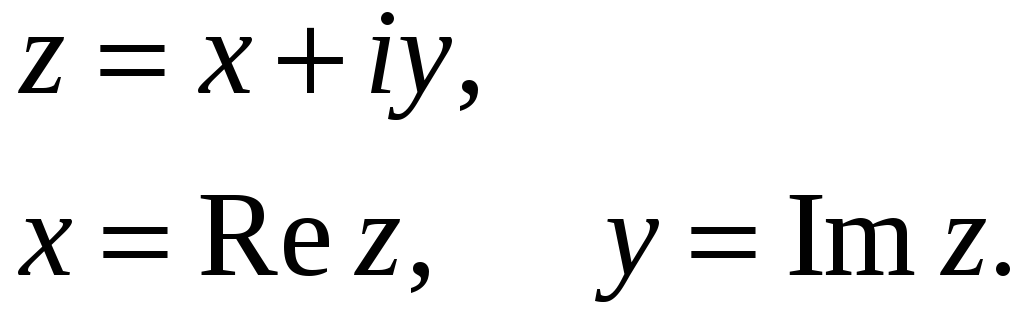. (12)

Комплексное число , у которого отлична от нуля мнимая часть, =, называют существенно комплексным числом.

Модулем комплексного числа (12) называют неотрицательное значение

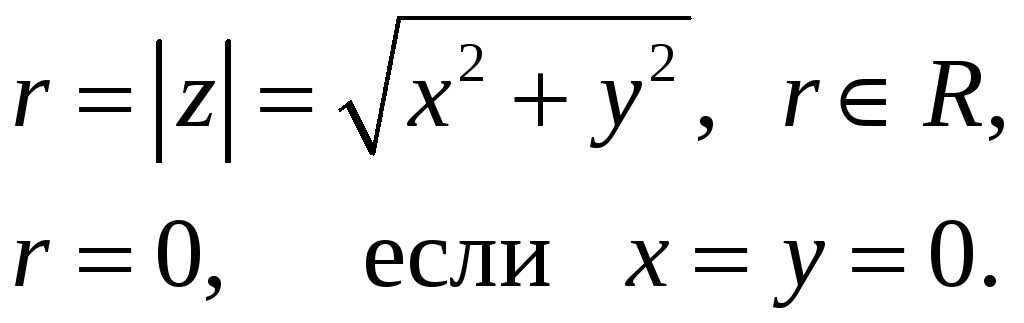(13)

Каждому комплексному числу, записанному в форме (12), соответствует упорядоченная пара вещественных чисел: . Её можно рассматривать и, как координаты точки на ортогональной декартовой плоскости , и, как декартовые координаты вектора , проведенного из начала ортогональной системы в точку . Наоборот каждой точке и, соответственно, вектору равенство (12) ставит в соответствие комплексное число , . Горизонтальную ось Ох «комплексной плоскости» обозначают , а мнимую ось Оу обозначают .

Угол , который радиус-вектор образует с положительной осью Ох, называют аргументом комплексного числа и обозначают . Поворот радиус вектора на угол даёт то же значение (12) комплексного числа. Поэтому значение для комплексного числа определяется с точностью до целочисленного значения , . Если значение аргумента комплексного числа такое, что , его обозначают . Ясно, что

, (14)

Поскольку период функции равен , что меньше 2 в (14), в применениях функции 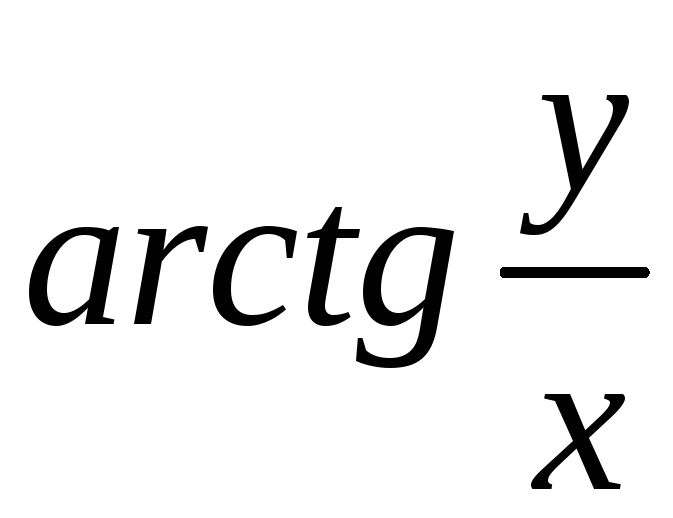для определения учитывается неоднозначность обратной тригонометрической функции :

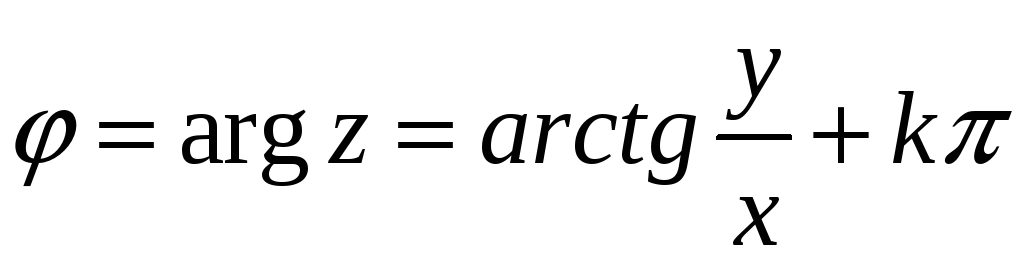, (15)

где , если точка находится в 1-ой и 4-ой четвертях, , если точка из второй четверти, и , когда точка находится в 3-ей четверти.

Для прямоугольного треугольника (см. ниже Рис. 1) можно записать очевидные тождества с тригонометрическими функциями и ,

, (16)

Их применение в (12) даёт тригонометрическую форму комплексного числа:

. (17)

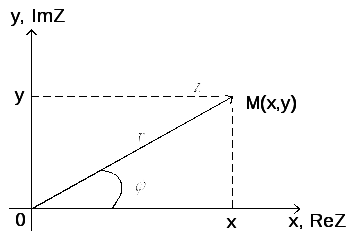
Рисунок 1.

Замена в (17) на , где , вследствие периодичности тригонометрических функций не изменяет значение числа .

Определение: Два комплексных числа равны, если, соответственно, равны их действительные и мнимые части.

После применения в (17) формулы Эйлера