
Лекция 1 _Комплексные числа / Комплексные числа
.doc
![]() ,
(18)
,
(18)
получим экспоненциальную, показательную, форму комплексного числа
![]() .
(19)
.
(19)
Формула (18) доказывается в теории рядов Тейлора. Она следует из равенства рядов, представляющих левую и правую части этого тождества. (Числовые и функциональные ряды изучаются во втором семестре).
Связь между
комплексными числами и векторами на
плоскости (с их проекциями на координатные
оси) становится полной после определения
операции сложения комплексных чисел,
![]() и
и
![]() :
:
![]() . (20)
. (20)
Разность комплексных
чисел определяется, как операция обратная
сложению:
![]() ,
где знак «
,
где знак «![]() »
обозначает «равносильность» равенств.
Отсюда
»
обозначает «равносильность» равенств.
Отсюда
![]() ,
,
![]() .
Решение этих уравнений даёт
.
Решение этих уравнений даёт
![]() (21)
(21)
Равенства (20) и (21) полностью совпадают с равенствами для проекций суммы и разности двух векторов, что иллюстрируют рисунки 2 и 3.
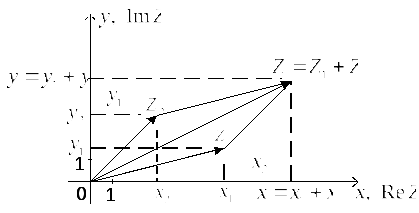
Рисунок 2.

Рисунок 3.
На рисунке 3 в точку
![]() направлен вектор
направлен вектор
![]() ,
который однозначно соответствует
разности комплексных чисел
,
который однозначно соответствует
разности комплексных чисел
![]() ,
определяемой по формуле (21). Взаимное
соответствие между комплексными числами
и векторами на плоскости, с точностью
до их сложения и вычитания, называют
изоморфизмом
множеств комплексных чисел и векторов
на плоскости.
,
определяемой по формуле (21). Взаимное
соответствие между комплексными числами
и векторами на плоскости, с точностью
до их сложения и вычитания, называют
изоморфизмом
множеств комплексных чисел и векторов
на плоскости.
Этот изоморфизм используется, например, в электротехнике. Расчеты сложных электрических цепей с равным успехом проводят и «методом векторных диаграмм», и «методом комплексных амплитуд». Результат тот же.
Произведение двух
комплексных чисел определяется как
алгебраическая операция умножения
двучлена
![]() на двучлен
на двучлен
![]() .
После учёта
.
После учёта
![]() и приведения подобных отдельно для
величин, не содержащих множителем мнимую
единицу
и приведения подобных отдельно для
величин, не содержащих множителем мнимую
единицу
![]() ,
и величин, содержащих её, получаем
,
и величин, содержащих её, получаем
![]() . (22)
. (22)
Применение
тригонометрической или показательной
форм записи чисел:
![]() ,
,
![]() подтверждает правило (22). Действительно,
для их произведения имеем
подтверждает правило (22). Действительно,
для их произведения имеем
 (23)
(23)
В (23) модуль числа
![]() равен произведению модулей перемножаемых
комплексных чисел,
равен произведению модулей перемножаемых
комплексных чисел,
![]() ,
а его аргумент φ
– сумме
аргументов,
,
а его аргумент φ
– сумме
аргументов,
![]() .
.
По правилу умножения
комплексных чисел (23) можем записать
m-ую
степень для комплексного числа
![]() :
:
![]() . (24)
. (24)
При
![]() из (24) следует известная формула Муавра:
из (24) следует известная формула Муавра:
![]() , (24′)
, (24′)
для любого целого
показателя степени
![]() .
.
Операция деления комплексных чисел
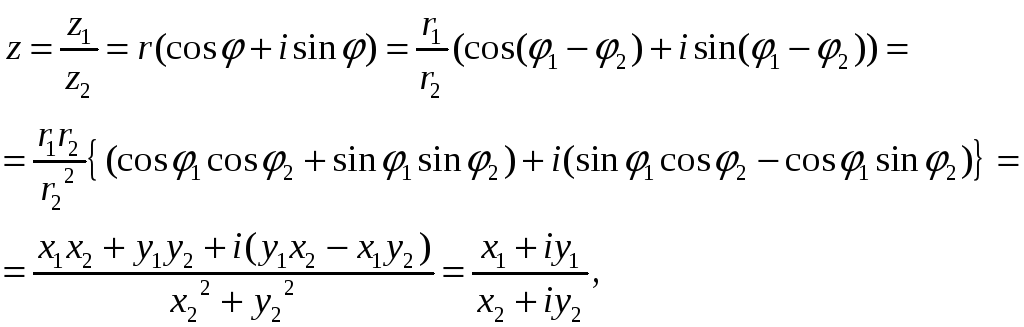 (25)
(25)
определяется
здесь, как операция обратная операции
умножения. Равенство
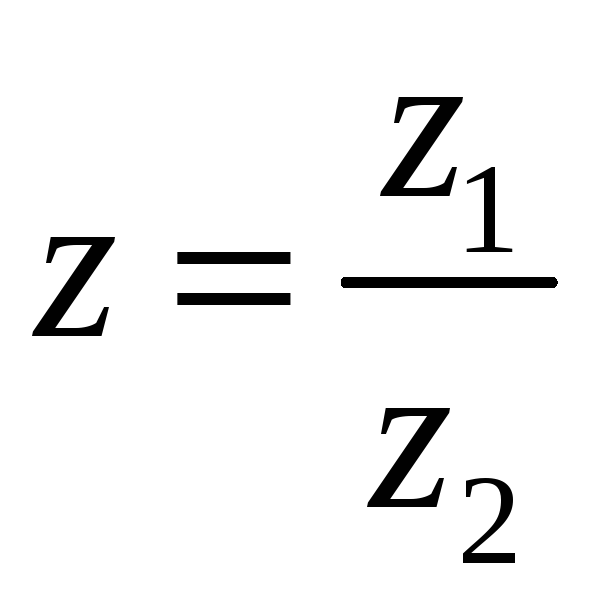 равносильно равенству
равносильно равенству
![]() .
Тогда
.
Тогда
![]() и
и
![]() .
Отсюда следует, что
.
Отсюда следует, что
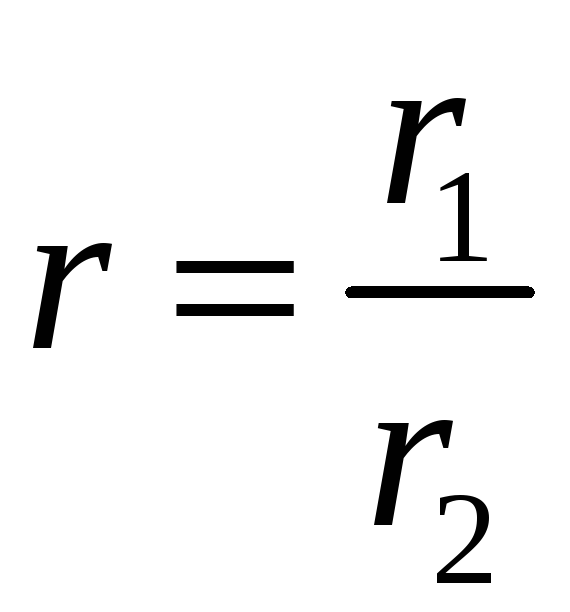 ,
,
![]() .
Поэтому для частного
.
Поэтому для частного
![]() комплексных чисел можем провести
преобразования (25).
комплексных чисел можем провести
преобразования (25).
При переходе к
координатной записи для результатов
деления (25) и умножения (23) комплексных
чисел применены равенства:
![]() ,
,
![]() ,
,
![]() и
и
![]() .
.
Операция «извлечение
корня» – это операция обратная «степени
числа». Но для комплексных чисел
извлечение корня любой степени является
не однозначной операцией.
То, что число
![]() является корнем
является корнем
![]() -ой
степени
-ой
степени
![]() из комплексного числа
из комплексного числа
![]() ,
равносильно
,
равносильно
![]() .
Отсюда для их модулей и аргументов
(сравни (18) и (24)) верны равенства:
.
Отсюда для их модулей и аргументов
(сравни (18) и (24)) верны равенства:
![]() ,
,
![]() . (26)
. (26)
Вследствие
неоднозначности
![]() и
и
![]() (см. (14)) тождество для аргументов в (26)
следует рассматривать, как равенство
множеств:
(см. (14)) тождество для аргументов в (26)
следует рассматривать, как равенство
множеств:
![]() ,
,
![]() . (27)
. (27)
Поэтому из первого уравнения (26) получаем одно значение модуля
![]() . (26′)
. (26′)
А из равенств (27)
имеем
![]() значений аргумента корня,
значений аргумента корня,
![]() ,
интервал изменения которого не превышает
,
интервал изменения которого не превышает
![]() .
Разные
.
Разные
![]() различает индекс
различает индекс
![]() :
:
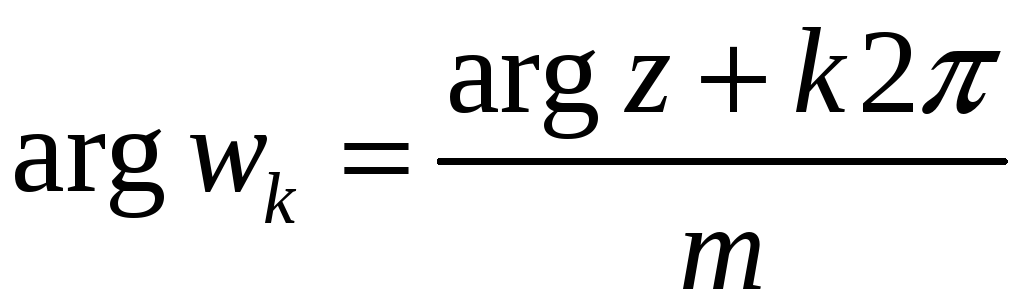 ,
,
![]() ,
где
,
где
![]() .
(27′)
.
(27′)
Общая формула для
![]() различных значений корня из комплексного
числа:
различных значений корня из комплексного
числа:
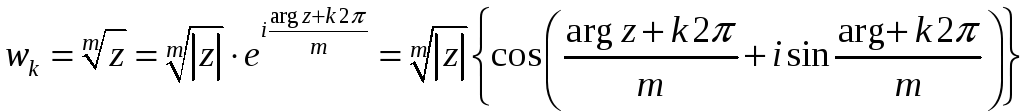 .
(28)
.
(28)
В ней
![]() .
Возведение каждого корня (28) в
.
Возведение каждого корня (28) в
![]() -ую
степень даёт
-ую
степень даёт
![]() .
Соединив начало координат плоскости
.
Соединив начало координат плоскости
![]() ,
где
,
где
![]() и
и
![]() ,
с точками
,
с точками
![]() ,
изображающими комплексные числа
,
изображающими комплексные числа
![]() (28), получим
(28), получим
![]() -конечную
звезду (см., например, ниже Рис. 4). Её лучи
равны, потому что у всех
-конечную
звезду (см., например, ниже Рис. 4). Её лучи
равны, потому что у всех
![]() одинаковые значения модуля
одинаковые значения модуля
![]() .
.
ПРИМЕРЫ:
Пример 1.
Для комплексного числа
 найти модуль и аргумент, записать его
в тригонометрическом и экспоненциальном
виде. Определить все корни 5-ой степени
из этого комплексного числа.
найти модуль и аргумент, записать его
в тригонометрическом и экспоненциальном
виде. Определить все корни 5-ой степени
из этого комплексного числа.
Решение.
Модуль числа равен:
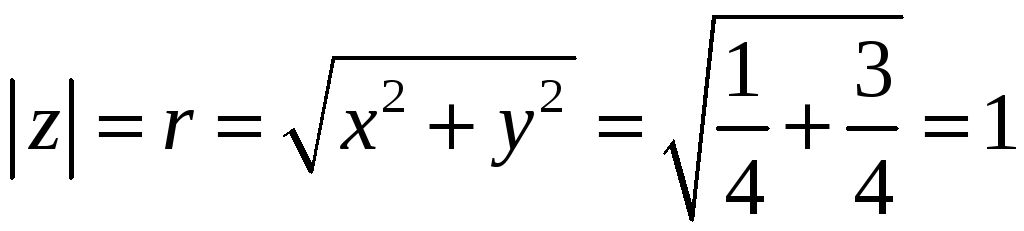
Так как
 ,
,
 и поэтому точка
и поэтому точка
![]() лежит в первой четверти, то в формуле
(15)
лежит в первой четверти, то в формуле
(15)
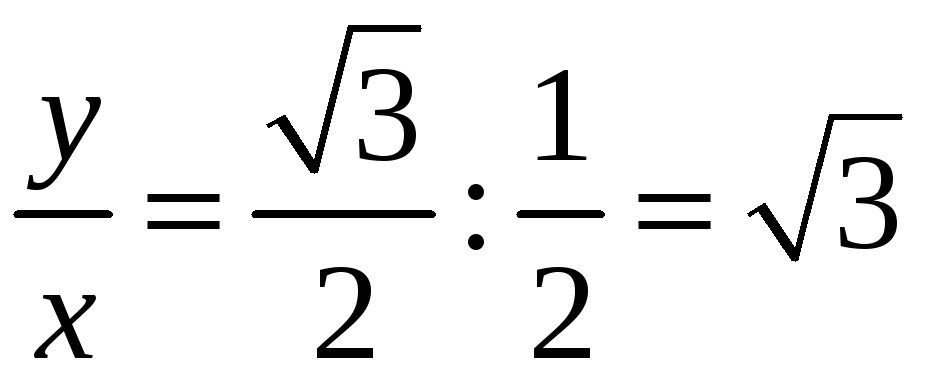 и
и
![]() :
:
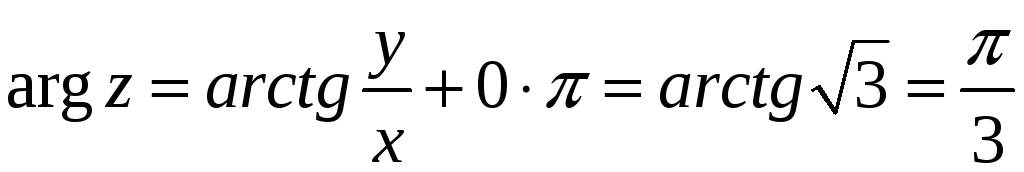 .
.
Запишем это число в тригонометрическом и экспоненциальном виде:
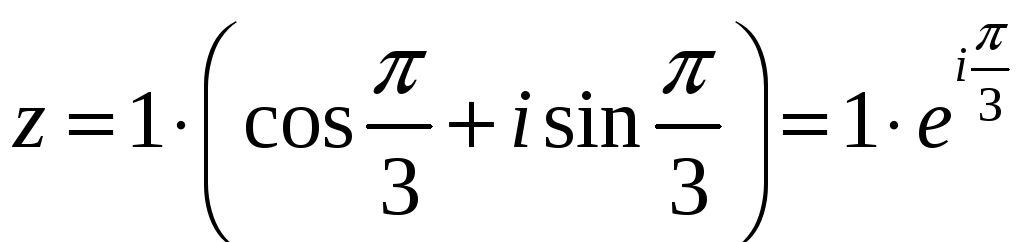 .
.
Вычислим модуль
для корня 5-ой степени из числа
![]() по формуле (26′)
по формуле (26′)
![]() .
.
По формуле (27′) мы
получим пять различных значений
аргумента, разность между которыми не
превышает
![]() ,
,
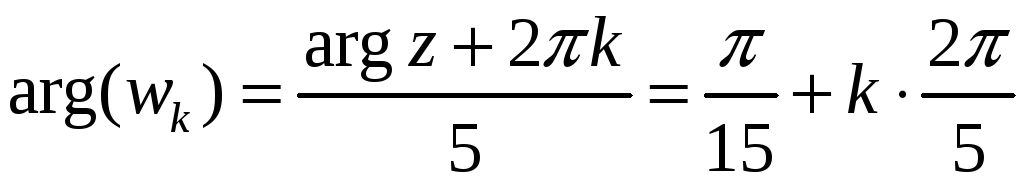 ,
,
![]() .
.
Из-за
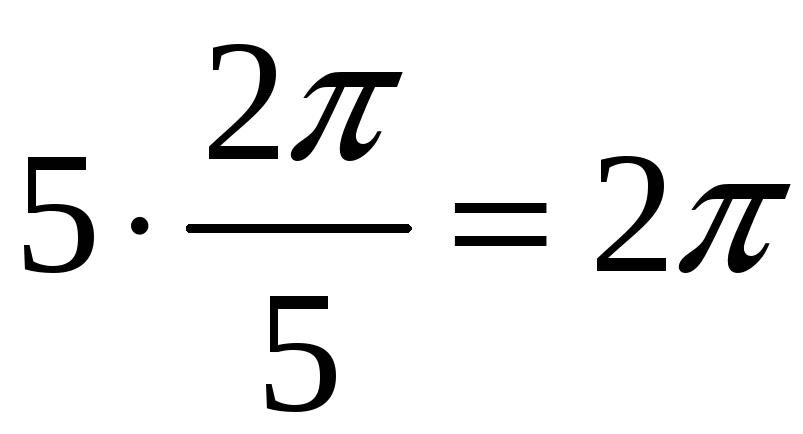 ,
значение корня с
,
значение корня с
![]() повторяет его значение с
повторяет его значение с
![]() :
:
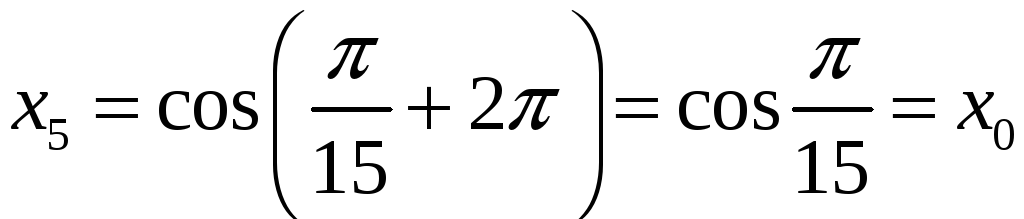 и
и
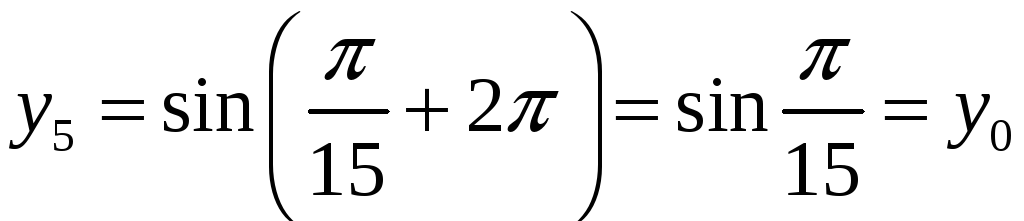 .
Равна и следующая пара корней. Поэтому
только 5 различных значений корня:
.
Равна и следующая пара корней. Поэтому
только 5 различных значений корня:
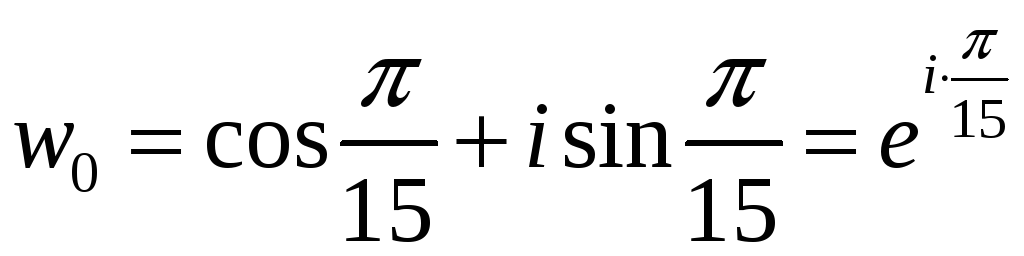 ,
,
 ,
,
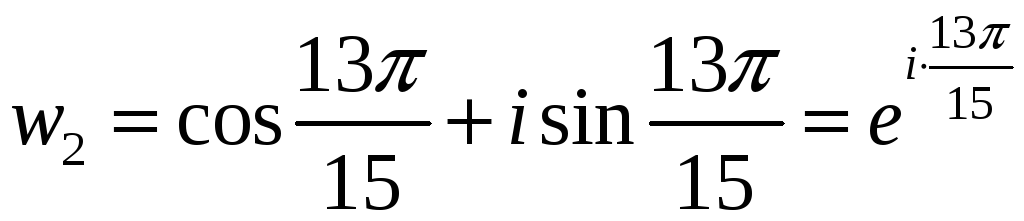 ,
,
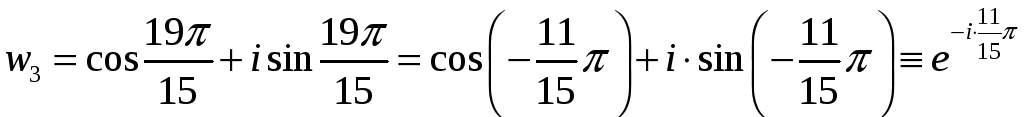 ,
,
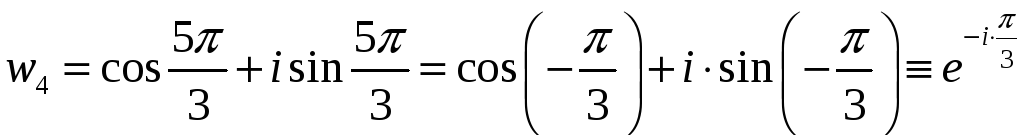 .
.
В записанных
формулах значения
![]() приведены к стандартному интервалу:
приведены к стандартному интервалу:
![]() ,
,
![]() .
Точки
.
Точки
![]() комплексной плоскости, соответствующие
комплексным числам
комплексной плоскости, соответствующие
комплексным числам
![]() ,
делят окружность радиуса
,
делят окружность радиуса
![]() с центром в начале координат на пять
равных дуг (см. Рис. 4).
с центром в начале координат на пять
равных дуг (см. Рис. 4).
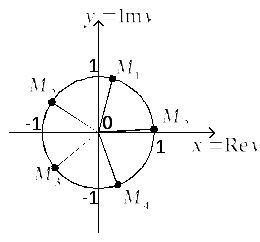
Рисунок 4.
Задача решена.
Операция комплексного
сопряжения (11) связана с заменой
![]() на
на
![]() .
Такой операции отвечает отражение
вектора
.
Такой операции отвечает отражение
вектора
![]() на Рис. 5 относительно оси
на Рис. 5 относительно оси
![]() .
После отражения он совпадает с вектором
.
После отражения он совпадает с вектором
![]() .
.
Комплексное
сопряжение над результатом каждого
арифметического действия равносильно
замене всех комплексных чисел, участвующих
в нём, на комплексно сопряженные числа.
Соответствующее отражение всех векторов
относительно оси
![]() для операции сложения проиллюстрировано
на Рис. 5. Отражение всех сторон
параллелограмма относительно оси Ох
приводит к отражению относительно этой
оси и всего параллелограмма (Рис. 5).
для операции сложения проиллюстрировано
на Рис. 5. Отражение всех сторон
параллелограмма относительно оси Ох
приводит к отражению относительно этой
оси и всего параллелограмма (Рис. 5).
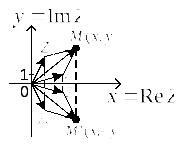
Рисунок 5.
Ниже приведены все тождества для арифметических операций, связанные с операцией комплексного сопряжения:
1)
![]() ,
,
2)
![]() ,
,
3)
![]() ,
,
4)
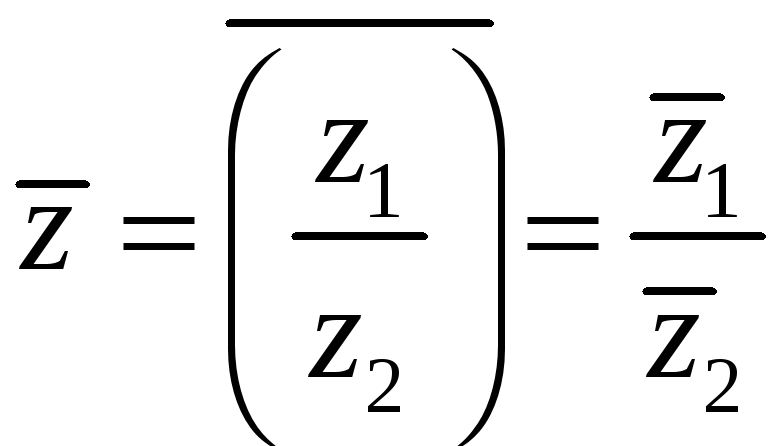 , (29)
, (29)
5)
![]() ,
,
6)
![]() ,
,
7)
![]() .
.
Тождество 1) и аналогично тождество 2) легко доказать геометрически, что и проиллюстрирует рисунок 5.
Тождества 3), 4), 5) и 6), 7) легко доказываются с помощью тригонометрической записи комплексного числа. Например,
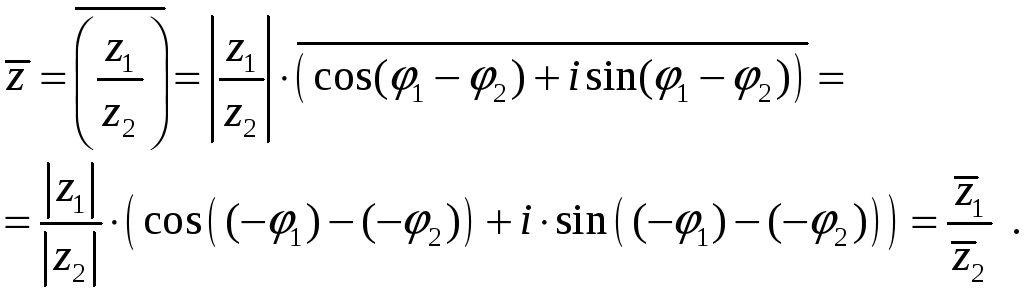
Другие функции комплексного аргумента будут рассмотрены позже.
Замечание:
При выполнении операций сложения и
вычитания удобнее применять координатную
запись комплексного числа,
![]() ,
а при умножении, делении, возведении в
степень или при извлечении корня из
комплексного числа удобнее применять
тригонометрическую или показательную
запись комплексного числа,
,
а при умножении, делении, возведении в
степень или при извлечении корня из
комплексного числа удобнее применять
тригонометрическую или показательную
запись комплексного числа,
![]() .
.
Равенство комплексных
чисел,
![]() ,
как и векторов,
,
как и векторов,
![]() ,
связано с равенством их координат:
,
связано с равенством их координат:
![]() и
и
![]() .
Равносильные им равенства:
.
Равносильные им равенства:
![]() и
и
![]() ,
,
![]() .
Изоморфные этим комплексным числам
вектора также равны, если равны их длины
и направления.
.
Изоморфные этим комплексным числам
вектора также равны, если равны их длины
и направления.
Замечание:
Из изоморфизма комплексных чисел и
векторов на плоскости следует, что
комплексные числа можно сравнивать
только по модулю. То есть можно проверить
выполнение неравенства
![]() или
или
![]() ,
но неравенства
,
но неравенства
![]() и
и
![]() не имеют
смысла. Это
нужно учитывать при решении уравнений
или неравенств, содержащих комплексные
числа.
не имеют
смысла. Это
нужно учитывать при решении уравнений
или неравенств, содержащих комплексные
числа.
«Принцип
перманентности»
Германа Хенкеля выполняется для множества
комплексных чисел. Поэтому оно является
допустимым расширением множества
вещественных чисел. Проверим это. Во
первых, множество комплексных чисел
содержит последовательность натуральных
чисел с у
= 0 и х
=
![]() :
:
![]() ,
,
![]() ,
.... Во вторых, для множества таких чисел,
из
,
.... Во вторых, для множества таких чисел,
из
![]() следует
следует
![]() ,
и
,
и
![]() верно при
верно при
![]() .
В третьих, схемы их сложения (20) и умножения
(22) переходят в схемы умножения
.
В третьих, схемы их сложения (20) и умножения
(22) переходят в схемы умножения
![]() и схемы сложения
и схемы сложения
![]() натуральных чисел, подчиняющиеся
перестановочному, сочетательному и
распределительному законам.
натуральных чисел, подчиняющиеся
перестановочному, сочетательному и
распределительному законам.
Пример 2.
Вычислить:
![]() ,
если
,
если
![]() .
.
Решение:
Для
![]() и
и
![]() число
число
![]() принадлежит четвертой четверти
комплексной плоскости и поэтому в
формуле (15)
принадлежит четвертой четверти
комплексной плоскости и поэтому в
формуле (15)
![]() :
:
 .
.
По определению (13):
![]() .
.
Теперь запишем
![]() в показательной и тригонометрической
форме:
в показательной и тригонометрической
форме:
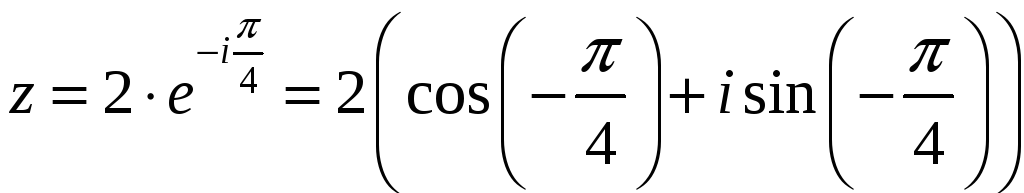 .
.
По правилу (24) вычислим так же степень комплексного числа:
![]()
Задача решена.
Пример 3.
Решить уравнение:
![]() .
.
Решение:
Пусть
![]() ,
тогда квадратное уравнение
,
тогда квадратное уравнение
![]() имеет дискриминант
имеет дискриминант
![]() .
.
Поэтому для него получим два комплексно сопряженных решения:
![]() ;
;
![]() ,
где
,
где
![]() .
.
Учитывая обозначение
![]() и формулу (28) для корня комплексного
числа получим три значения
и формулу (28) для корня комплексного
числа получим три значения
![]() ,
,
![]() и
и
![]() для кубического корня из
для кубического корня из
![]() и три значения
и три значения
![]() ,
,
![]() ,
,
![]() для кубического корня из комплексного
числа
для кубического корня из комплексного
числа
![]() .
.
Для
![]() :
:
![]() ,
,
![]() -ой
четверти, в формуле (13)
-ой
четверти, в формуле (13)
![]() и поэтому
и поэтому
 .
.
По формулам (28) получаем:
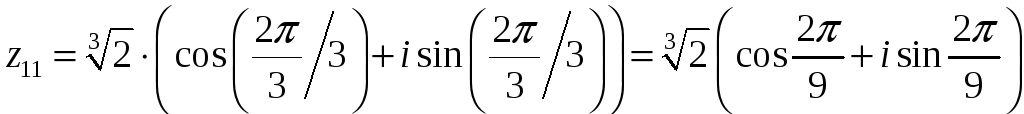 ,
,
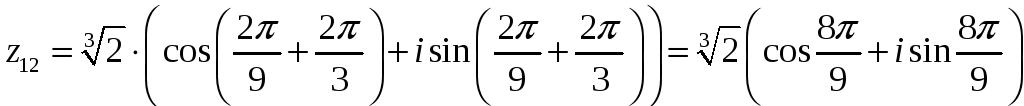 ,
,
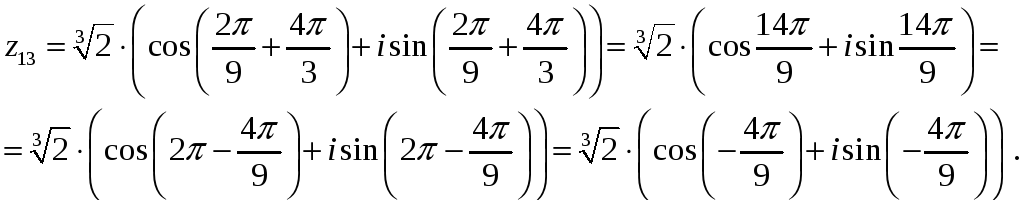 Здесь
учтено стандартное ограничение на
допустимые значения
Здесь
учтено стандартное ограничение на
допустимые значения
![]() :
:
![]() .
.
Решая аналогичное
уравнение
![]() ,
получаем что
,
получаем что
![]() ,
,
![]() -ей
четверти, в (13)
-ей
четверти, в (13)
![]() и
и
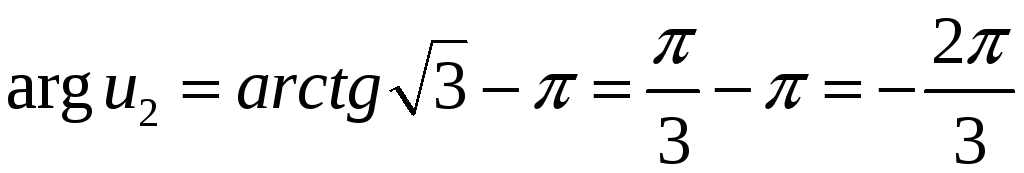 .
.
В этом случае из формул (28) следует:
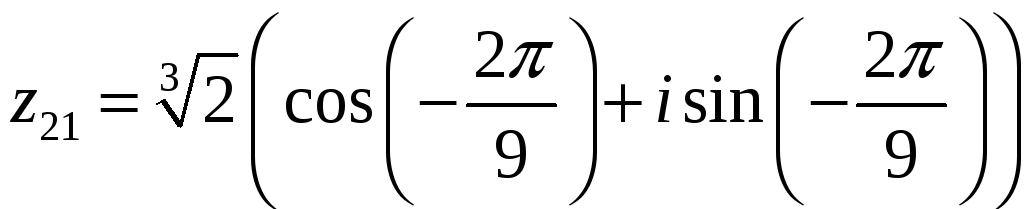 ,
,
 ,
,
 .
.
Всем решениям
уравнения отвечают точки, лежащие на
круге радиуса
![]() с центром в начале координат комплексной
плоскости (см. Рис. 6).
с центром в начале координат комплексной
плоскости (см. Рис. 6).
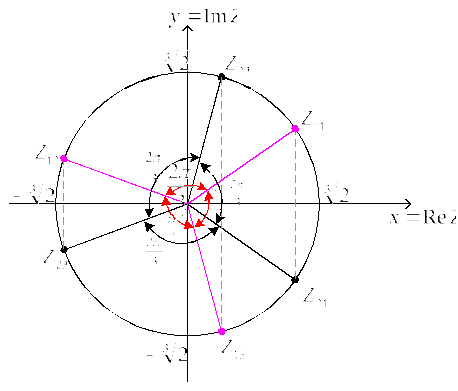
Рисунок 6.
Задача решена.
Пример 4. Решить
неравенство:
![]() .
.
Решение:
Такое неравенство имеет смысл, если его можно свести к неравенству для модуля комплексного числа.
Учитывая, что
согласно (10)
![]() и
и
![]() ,
получим неравенство
,
получим неравенство
![]() .
Оно не содержит мнимой единицы и
превращается в неравенство только для
вещественных координат точек плоскости,
которое ограничивает их допустимые
значения:
.
Оно не содержит мнимой единицы и
превращается в неравенство только для
вещественных координат точек плоскости,
которое ограничивает их допустимые
значения:
![]() .
.
Выделяя полные квадраты, получим эквивалентное неравенство
![]() , (*)
, (*)
Оно эквивалентно
неравенству
![]() для модуля комплексного числа
для модуля комплексного числа
![]() ,
поэтому неравенство (*) имеет решение.
,
поэтому неравенство (*) имеет решение.
В случае равенства в (*) из него следует уравнение окружности
![]() (**)
(**)
радиуса
![]() с координатами её центра:
с координатами её центра:
![]() ,
,
![]() .
Отсюда ясно, что неравенству (*)
удовлетворяют все точки круга,
ограниченного окружностью (**), включая
его границу (см. ниже Рис. 7).
.
Отсюда ясно, что неравенству (*)
удовлетворяют все точки круга,
ограниченного окружностью (**), включая
его границу (см. ниже Рис. 7).
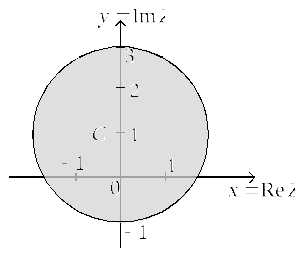
Рисунок 7.
Задача решена.
