Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Mat_modeli_OSA_lab_rab

.pdf

Скачиваний:

Добавлен:

03.03.2016

Размер:

1.01 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Таблица 2.1. Исходные данные

№

Исходное нелинейное уравнение

y(t)

+ 5(y(t))3 = 3(u(t))2 +

du(t)

dt2

y(t)

dy(t)

u(t)

+ 3

= 4 u(t) +

y(t)

dt2

0,5

dy(t)

0,5

= 4

u(t)

du(t)

y2 (t)

u(t)

y(t)

+ 1,5

dy(t)

0,1

u(t)

+ 3

u(t)

du(t)

dt3

y4 (t)

dt2

u3 (t)

y(t)

+ y4 (t) =

u(t)

+ 3

du(t)

dt3

dt2

3 (t)

dy(t)

0,5

u3 (t)

du(t)

d 2 y(t)

y(t)

u(t)

dt2

y(t)

+ 0,5

dy(t)

(y(t))

= 4(u(t))3 +

du(t)

dt2

2u(t)

y(t)

dy(t)

du(t)

= u(t) +

ey(t)

dt2

1,5

y(t)

+ 3

dy(t)

u(t)

+ 4

du(t)

dt2

y3 (t)

2 u(t)

y(t)

u(t)

y(t)

du(t)

+ 0,5

= 3

dt3

dt2

u2 (t)

dt2

y3 (t)

0,8

dy(t)

y2 (t)

u3 (t)

+ 1,8

du(t)

d 2 y(t)

u(t)

y(t)

0,9

y(t)

dy(t)

y(t)

+ 2

du(t)

3eu(t)

dt2

u(t)

dy(t)

3u(t)

= 4

y(t)

du(t)

+ 5

y(t)

y2 (t)

lnu(t)

dt2

Окончание таблицы 2.1

2,5

y(t)

+ 1,5

dy(t)

u(t)

+ 3

du(t)

dt2

u(t)

(y(t))2

y(t)

+ 3,5

dy(t)

(y(t))

= 5ln(u(t))3 +

du(t)

+ 3

u(t)

dt2

2u(t)

y(t)

dy(t)

+ 3y(t)eu(t)

du(t)

u(t)

1,6

= ln

u(t) + 2

+ 0,5

dt2

2 d

y(t)

+1,5 dy(t) +

u(t)

= y(t)u(t) + d

u(t)

dt2

y(t)

dt2

y(t)

du(t)

+ u(t)(y(t))2 = 2 u(t) +

dt2

y(t)

dy(t)

+ u(t)ln y(t) = 3eu(t)

du(t)

dt2

0,5

y(t)

+ 4

dy(t)

lnu(t)

= eu(t) (y(t))2 + 2

du(t)

dt2

3y(t)

Л А Б О Р А Т О Р Н А Я Р А Б О Т А 3

ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ОБЪЕКТОВ АВТОМАТИЗАЦИИ

Ц Е Л Ь Р А Б О Т Ы - исследование временных характеристик линейных систем автоматического управления.

3.1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

Дифференциальное уравнение является самой общей формой описания элемента и не дает наглядного представления о передаточных свойствах элемента. Наглядное представление об этих свойствах дает функция y(t), являющаяся решением дифференциального уравнения. Но одно и тоже дифференциальное уравнение может иметь множество решений, конкретный вид которых зависит от начальных условий и от характера функции x(t), т.е. от начального состояния элемента и вида внешнего воздействия. Поэтому

динамические свойства элементов и систем принято характеризовать решением дифференциального уравнения, которое соответствует нулевым начальным условиям и одному из типовых воздействий.

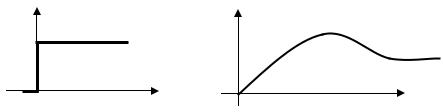
Наиболее наглядное представление о динамических свойствах элемента дает его переходная функция (характеристика).

Переходной функцией h(t) называют изменение выходной величины y(t) во времени, возникающее после подачи на вход единичного ступенчатого воздействия при нулевых начальных условиях.

x(t)

y(t)

1(t)

h(t)

0
	0

Переходная функция может быть задана графически или аналитически. Формульное выражение функции h(t) для конкретного элемента можно найти,

решая его дифференциальное уравнение при

x(t) = 1(t) и y(-0) = y’(-0) = y”(-0)… = y(n-1)(-0) = 0

Это условие означает, что выходная величина y(t) и ее производные до (n-1)-го порядка непосредственно перед подачей ступенчатого воздействия равен нулю.

Переходная функция h(t) имеет две составляющие: вынужденную hв(t) и свободную составляющую hс(t).

Вынужденная составляющая hв(t) переходного процесса представляет собой частное решение исходного уравнения. При ступенчатом воздействии

вынужденная составляющая равна установившемуся значению выходной величины, которое может быть определено из дифференциального уравнения:

hв (t) = y(∞ ) = bm . an

Свободная составляющая hс(t) может быть найдена как решение соответствующего однородного дифференциального уравнения в виде:

	n	C		p t
h (t) = å		C		e k
c	k=1		k
	k=1		k

где pk - корни характеристического уравнения

Ck – постоянные интегрирования, зависящие от начальных условий

Характеристическое уравнение данного дифференциального уравнения представляет собой алгебраическое уравнение, степень и коэффициенты

которого совпадают с порядком и коэффициентами левой части этого дифференциального уравнения. Для дифференциального уравнения (2) характеристическое уравнение имеет вид:

a0 pn + a1 pn −1 + ...+ an = 0

Для линейных систем справедливо следующее общее правило: реакция y(t) на неединичное ступенчатое воздействие a*1(t) равна произведению переходной функции h(t) на величину множителя a, т.е. y(t) = ah(t).

Импульсной переходной функцией w(t) называют изменение выходной величины y(t), возникающее после передачи на вход дельта-функции, при нулевых начальных условиях.

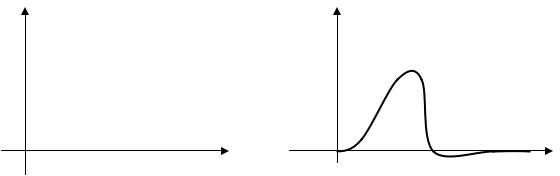
x(t) y(t)


	σ (t) = x(t)			w(t)
	σ (t) = x(t)
					t
		t

0			0

Если входное воздействие представляет собой неединичный импульс aσ (t), то ординаты функции выходной величины y(t) , будут в a раз больше ординат функции w(t), т.е. y(t) = aw(t).

Связь между переходной и импульсной переходной функциями h(t) и w(t) существует следующая взаимосвязь:

	dh(t)		t
w(t) =		,	h(t) = ò w(τ )dτ .
	dt
			0

При помощи импульсной переходной функции элемента можно определить ее реакцию на входное воздействие произвольного вида. Связь

между изменениями входной и выходной величин во времени устанавливается интегралом свертки:

	y (t ) =	∞	x (τ ) w (t - τ ) w (τ ) d τ =		∞	x (t - τ ) w (τ ) d τ .
	y (t ) =	ò	x (τ ) w (t - τ ) w (τ ) d τ =		ò	x (t - τ ) w (τ ) d τ .
		0			0
Второе	распространенное			название		функции	w(t) – весовая.

Действительно, эта функция определяет вес (долю), с которым каждый входной импульс, полученный при разложении сигнала x(t), участвует в формировании результирующего выходного сигнала y(t).

В данной работе, используя моделирование, получают переходную h(t) и весовую w(t) функции объектов управления различного порядка и структуры.

Экспериментальные исследования заключаются в следующем. На вход САУ подается сигнал в виде единичной ступенчатой функции. На выходе системы регистрируется ее реакция на данное входное воздействие. При подаче на вход САУ d – функции, на ее выходе регистрируется весовая функция. По

полученным графикам переходной и весовой функций можно определить параметры данного объекта управления, а также оценить эффективность управления в САУ.

3.2. МОДЕЛИРОВАНИЕ ВРЕМЕННЫХ ХАРАКТЕРИСТИК С ИСПОЛЬЗОВАНИЕМ SIMULINK

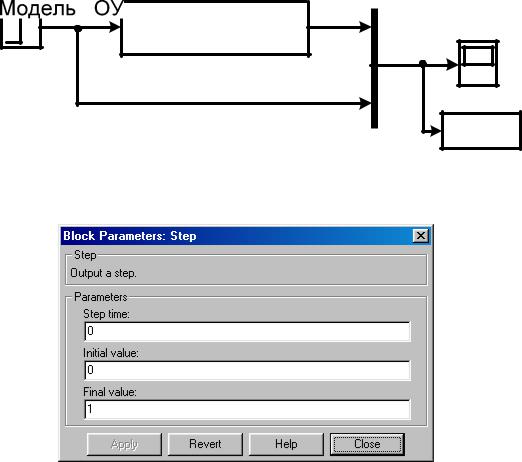
На рис. 3.1 представлена схема моделирования для получения переходных характеристик типовых звеньев с использованием пакета simulink.

Рисунок 3.1. Схема получения переходных характеристик.

Рисунок 3.2. Установка параметров входного ступенчатого воздействия

Для получения переходной характеристики на вход модели объекта подается ступенчатое воздействие, параметры которого задаются в блоке Step (рис. 3.2).

Вместо блока «модель ОУ» (рис. 3.1) в схему моделирования вставляется

модель исследуемой системы, структурные схемы которых приведены ниже

(рис.)

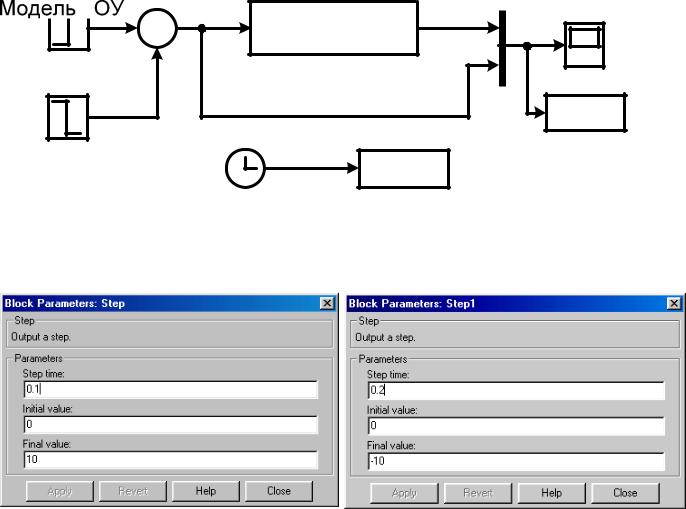
На рис. 3.3 представлена схема моделирования для получения импульсных переходных характеристик с использованием пакета simulink.

Особенность данной схемы заключается в формировании единичного импульса, для получения которого применяются три блока: два блока Step и один блок суммирования - Sum (рис. 3.3). Параметры блоков Step и Step1 задаются согласно рис. 3.4.

Рисунок 3.3. Схема получения импульсных переходных характеристик

Рисунок 3.4. Установка параметров единичного импульсного воздействия

3.3. СОСТАВЛЕНИЕ МОДЕЛИ ПО ЗАДАННОМУ

ДИФФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ ОБЪЕКТА

Составление модели рассмотрим на примере системы 3-го порядка, которая описывается следующим дифференциальным уравнением:

d 3 y(t)

+ a

d 2 y(t)

+ a

dy(t)

+ a

y(t) = b

d 3u(t)

+ b

d 2u(t)

+ b

du(t)

+ b u(t) .

dt3

2 dt

dt3

dt2

1 dt2

или

a0 y′′′(t) + a1 y′′(t) + a2 y′(t) + a3 y(t) = b0u′′′(t) + b1u′′(t) + b2u′(t) + b3u(t) .

(*)

Перенесем слагаемые с производными влево, а без производных – вправо:

a0 y′′′(t) + a1 y′′(t) + a2 y′(t) − b0u′′′(t) − b1u′′(t) − b2u′(t) = b3u(t) − a3 y(t) .

В левой части вынесем знак дифференцирования и введем

промежуточную переменную x1(t) :

(a0 y′′(t) + a1 y′(t) + a2 y(t) − b0u′′(t) − b1u′(t) − b2u(t)) = b3u(t) − a3 y(t) .

(3.1)

x1(t)

x1′(t)

x1′ (t) = b3 u(t) − a3 y(t) .

(3.2)

Из уравнения (3.1):

a0 y′′(t) + a1 y′(t) + a2 y(t) − b0u′′(t) − b1u′(t) − b2u(t) = x1(t) .

Перенесем слагаемые с производными влево, а без производных – вправо: a0 y′′(t) + a1 y′(t) − b0u′′(t) − b1u′(t) = x1(t) − a2 y(t) + b2u(t) .

В левой части вынесем знак дифференцирования и введем

промежуточную переменную x2 (t) :
	d	(a0 y′(t) + a1 y(t) − b0u′(t) − b1u(t)) = x1(t) − a2 y(t) + b2u(t).	(3.3)
	dt		(3.3)
		x2 (t)
		′
		x2 (t)
	′	(t) = x1 (t) − a2 y(t) + b2u(t) .	(3.4)
	x2	(t) = x1 (t) − a2 y(t) + b2u(t) .	(3.4)

Из уравнения (3.3):

a0 y′(t) + a1 y(t) − b0u′(t) − b1u(t) = x2 (t) .

Перенесем слагаемые с производными влево, а без производных – вправо: a0 y′(t) − b0u′(t) = x2 (t) − a1 y(t) + b1u(t)

В левой части вынесем знак дифференцирования и введем

промежуточную переменную x3 (t) :

y(t) - b u(t)) = x

(t) - a y(t) + b u(t) .

(3.5)

x3 (t)

′

(t)

′

(t)

= x2 (t) − a1 y(t) + b1u(t)

(3.6)

Из уравнения (3.6):

a0 y(t) − b0u(t) = x3 (t)

Из последнего уравнения выразим y(t):

y(t) =

x3 (t) +

u(t)

(3.7)

Уравнение (3.7) связывает выходную переменную y(t) с входной u(t) и промежуточной переменной x3 (t) .

Подставим уравнение (3.7) в (3.2), (3.4), (3.6) и получим следующую

систему уравнений:

ì	a3
ïx1¢(t) = -	a3		x3 (t) + (b3
ïx1¢(t) = -			x3 (t) + (b3
ï	a0
ï				a2
íx2¢ (t) = x1		(t) -		a2		x3 (t)
íx2¢ (t) = x1		(t) -				x3 (t)
ï				a0
ï					a1
ïx3¢ (t) = x2		(t) -			a1	x3 (t)
ïx3¢ (t) = x2		(t) -				x3 (t)
î					a0

- a3 b0 )u(t) a0

+ (b	- a			b0		)u(t)	(3.8)

2		2 a0
+ (b - a			b0		)u(t)

1	1 a0

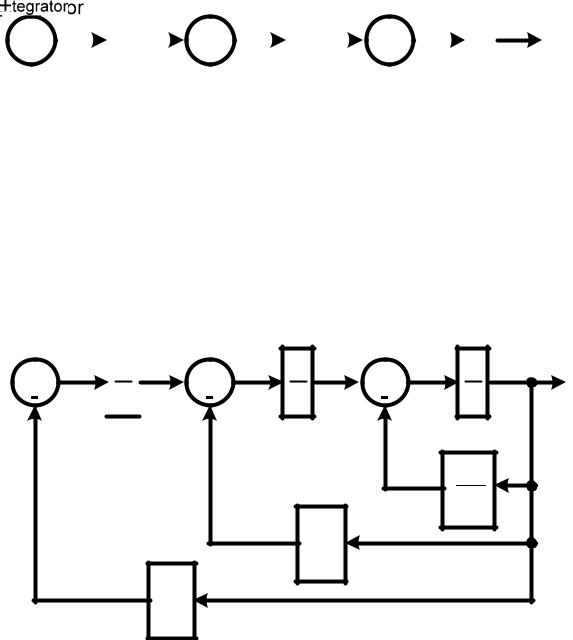
Система (3.8) и уравнение (3.7) позволяют построить структуру модели исходного дифференциального уравнения. Прямая цепь модели состоит из трех интеграторов, к входу каждого из которых подключен выход сумматора (согласно системе (3.8)) (рис.3.5). На выходе каждого сумматора получается

соответствующая промежуточная переменная x1(t) ,

x2 (t) , x3 (t) .

′

Рисунок 3.5. Первый этап формирования модели.

		Согласно уравнениям системы (3.8) формируем связь через
соответствующие				коэффициенты между переменной x3 (t) и производными
′	(t) ,	′	′	(рис.3.6).
x1		x2 (t) ,	x3 (t)

x1′

a3 a0

x′	′
x′	x3
2
	a1
	a0
	a2
	a0

Рисунок 3.6. Второй этап формирования модели.

		Согласно уравнениям системы (3.8) формируем связь через
соответствующие				коэффициенты между переменной u(t)		и производными
′	(t) ,	′	′	(рис.	3.7).
x1		x2 (t) ,	x3 (t)
		Последний		этап	формирования модели - согласно	уравнению (3.8)

формируем связь через соответствующие коэффициенты между переменной y(t) и переменными u(t) и x3(t) (рис. 3.8).

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.03.20164.5 Mб276Manual_Maxwell_render.pdf
#
03.03.20161.44 Mб17matem_2_chast.pdf
#
03.03.2016626.51 Кб24MathCad_Metoda_Lab.pdf
#
03.03.20168.37 Mб25Mathematics of Economics and Business.pdf
#
03.03.20162.72 Mб17Mat_modeli_OSA_konspekt_lektsiy.pdf
#
03.03.20161.01 Mб20Mat_modeli_OSA_lab_rab.pdf
#
03.03.20166.75 Mб13Metodicheskie_ukazania.doc
#
03.03.20161.58 Mб11Metodicheskie_ukazania_ind.doc
#
03.03.20161.54 Mб3Metodicheskie_ukazania_prakt.doc
#
03.03.20161.46 Mб30Metodichka-TAiFYa.doc
#
03.03.201614.77 Mб51Metodichka.doc