- •6.050903 «Телекомунікаційні системи та мережі»
- •Цель, задача и виды расчетов надежности электронных устройств
- •Лабораторная работа №1
- •Расчет ремонтопригодности устройства
- •Расчет зип (запас инструментов и принадлежностей)
- •Задание на проведение лабораторной работы
- •Лабораторная работа №2
- •Задание на проведение лабораторной работы
- •Лабораторная работа №3 Расчет показателей надежности системы с учетом графа состояний
- •Задание на проведение лабораторной работы
- •Рекомендуемая литература
Лабораторная работа №3 Расчет показателей надежности системы с учетом графа состояний
В качестве примера, проведемрасчет показателей надежности для микропроцессорной системы контроля(МПС) и управления работой азотного компрессора.
Согласно техническомузаданиюМПС контроля должна иметь следующие показатели надежности:
средняя наработка на отказ - не менее 10000 ч;
вероятность безотказной работы - 0,95;
среднее время восстановления - не более 1,5 ч.
Устройство в процессе эксплуатации может находиться в трех состояниях:
1 – полностью трудоспособное состояние (происходит определение значения технологических параметров газа, работает система вычисления погрешности и работает блок индикации);
2 – частичная трудоспособность (происходит процесс контроля, но цепь индикации не работает);
 3
– состояние отказа (основная функция
не выполняется). При переходе системы
из первого состояния в состояние 2 или
3 вырабатывается восстановление полной
трудоспособности. Граф переходов системы
контроля и управления с одного состояния
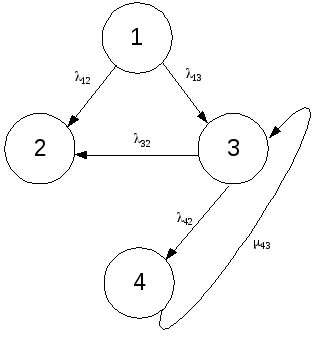
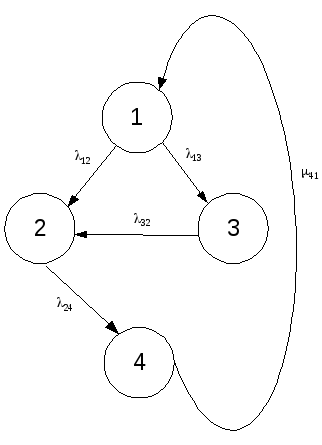
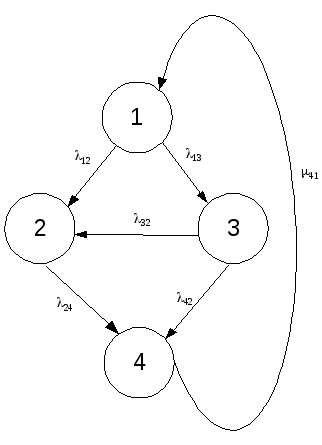
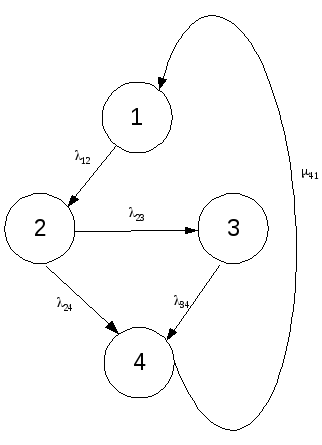
в другое показан на рисунке 1.
3
– состояние отказа (основная функция
не выполняется). При переходе системы
из первого состояния в состояние 2 или
3 вырабатывается восстановление полной
трудоспособности. Граф переходов системы
контроля и управления с одного состояния
в другое показан на рисунке 1.
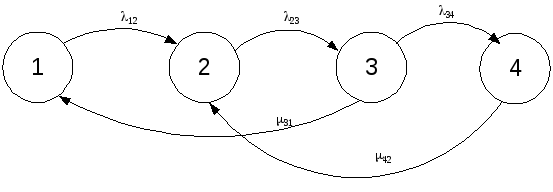
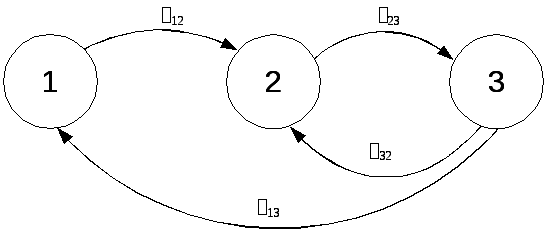
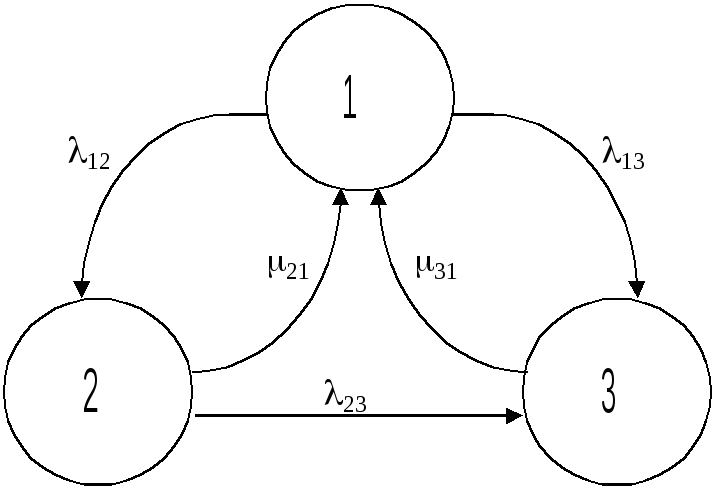
Рисунок 1 – Граф состояний МПС
12 – интенсивность отказов блока индикации;
13 – интенсивность отказов МПС;
23 – интенсивность отказов системы контроля после отказа блока индикации;
31 – плотность вероятности восстановления первостепенной функции;
21 – интенсивность восстановления блока индикации.
Для описания графа состояний установки системой дифференциальных уравнений (ДУ), используем правило Колмогорова. Получим следующее:
 (16)
(16)
В тех случаях, если во время расчета учитываются процессы восстановления, потоки отказов являются марковскими стационарными. В этом случае вероятность пребывания устройства в том, или ином состоянии не зависит от времени. Уравнения системы (16) зависимые, поэтому третье уравнение заменено на выражение Р1+Р2+Р3=1, тогда система (16) принимает вид:
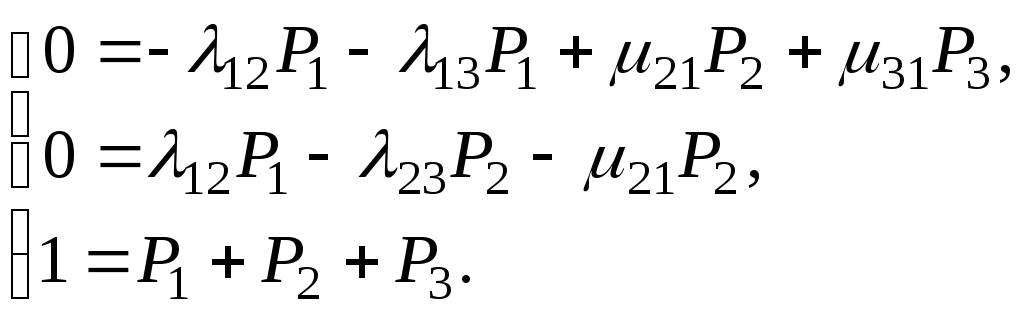 (17)
(17)
Полученную систему можно решить относительно Рi.
Решив систему относительно Рі, найдем вероятности пребывания системы в каждом из состояний:
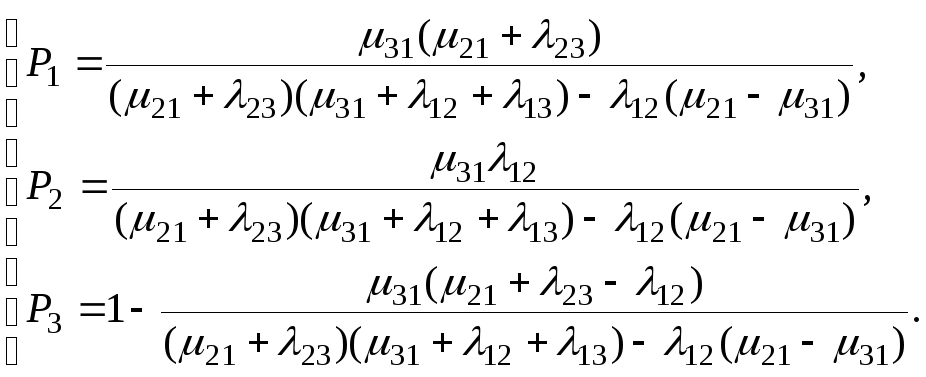 (18)
(18)
Для определения времени пребывание системы в одном из состояний, в (16) члены, связанные с третьим состоянием, исключены; сделана замена Рi(t) = Ti, в результате чего получаем систему:
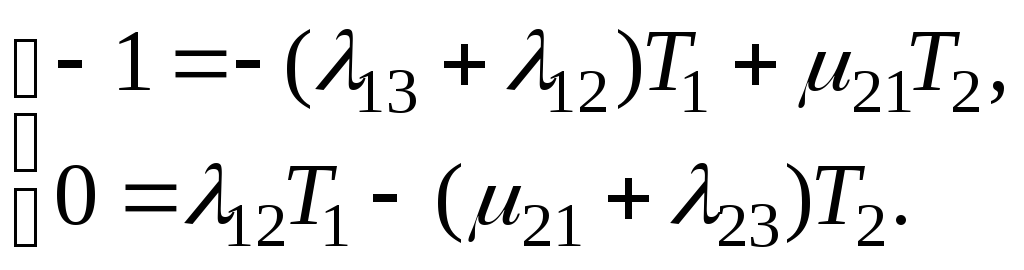 (19)
(19)
Решив полученную систему относительно Т1 и Т2, найдем:
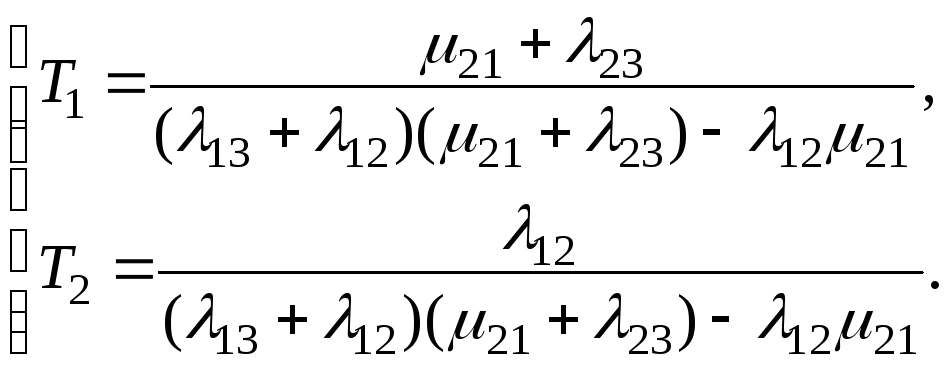 (20)
(20)
Для нахождения значений Р1, Р2, Р3, Т1, Т2 выполняется расчет значений 12, 13, 23, 21, 31 приближенным или уточненным методом. Однако в рамках данной лабораторной работы указанные параметры будут заданы.
Задание на проведение лабораторной работы
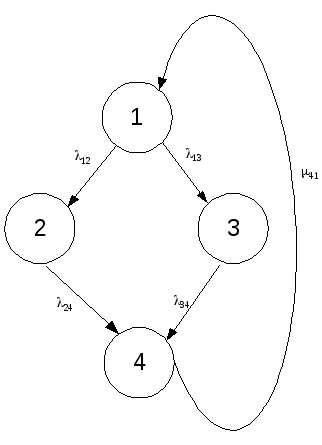
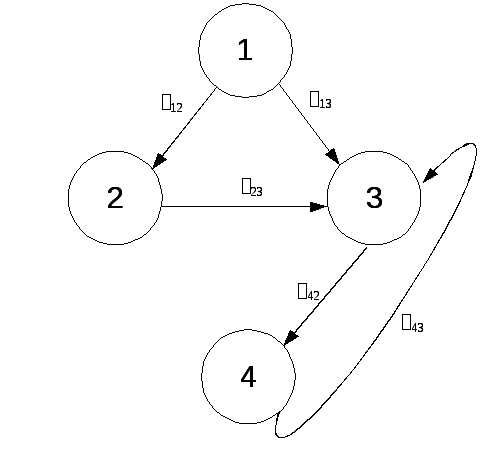
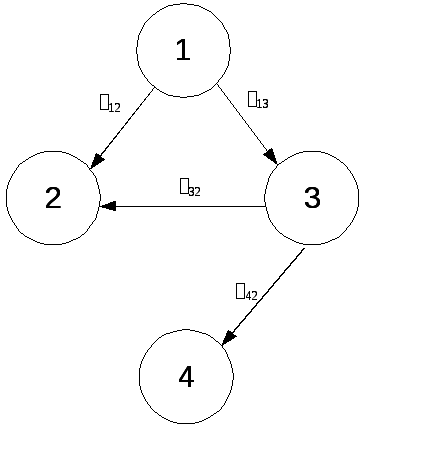
Определить вероятность безотказной работы за 2000 часов и среднюю наработку объекта на отказ для предложенного графа с заданными интенсивностями:
|
Вариант 1
|
Вариант 2
Вариант 3
|
Вариант 4
Вариант 5
|
Вариант 6
Вариант 7
|
Вариант 8
Вариант 9
|
Вариант 10
Вариант 11
|
Вариант 12
|
|
12=1·10-3 1/ч 13=1·10-4 1/ч 23=1·10-5 1/ч 24=5·10-3 1/ч 34=1·10-3 1/ч 32=5·10-4 1/ч 21= 0,5 1/ч 31= 0,7 1/ч 41= 0,1 1/ч 32= 0,5 1/ч 43= 0,2 1/ч
|
Вариант 13
|
|
12=5·10-4 1/ч 13=1·10-3 1/ч 23=1·10-2 1/ч 24=1·10-4 1/ч 34=5·10-3 1/ч 32=5·10-4 1/ч 21= 0,9 1/ч 31= 0,5 1/ч 41= 0,5 1/ч 32= 0,7 1/ч 43= 0,1 1/ч
|
Вариант 14
Вариант 15
|