
Лекции СТАТИСТИКА
.pdf
ПОСТРОЕНИЕ РЯДОВ РАСПРЕДЕЛЕНИЯ
Ряд распределения – это упорядоченное распределение выборки на группы по определенному варьирующему признаку. Ряд распределения принято оформлять в виде таблиц.
АТРИБУТИВНЫЕ РЯДЫ РАСПРЕДЕЛЕНИЯ
Это ряды распределения, построенные по номинальным признакам. В качестве примера рассмотрим распределение респондентов согласно их семейномуположению (Табл. 2).
Табл. 2. Распределение респондентов по семейному положению (чел.).
№ п/п |
Категория занятости работника |
Количество респондентов |
1 |
Полная занятость |
747 |
2 |
Частичная занятость |
161 |
3 |
Безработный |
32 |
4 |
Временно не работает |
51 |
5 |
Пенсионер(ка) |
231 |
6 |
Учащийся |
42 |
7 |
Домохозяйка(ин) |
200 |
8 |
Нет ответа |
36 |
|
Всего |
1500 |
Графически атрибутивные ряды распределения можно представить в виде столбчатой или круговой диаграммы (Рис. 2, Рис. 3).
Частота
800
600
400
200
0
Полная занятость |
Частичная занятость |
Безработный |
Временно не работает |
Пенсионер (ка) |
Учащийся |
Домохозяйка (ин) |
Домохозяйка (ин)
Учащийся
Пенсионер (ка)
Полная занятость
Временно не работает
Безработный
Частичная занятость
Рис. 2. Столбчатый график |
Рис. 3. Круговая диаграмма |
ВАРИАЦИОННЫЕ РЯДЫ РАСПРЕДЕЛЕНИЯ
Это ряды распределения, построенные по порядковым и количественным признакам. Такой ряд представляет собой характеристикувариантов признака их частотами.
Вариантами считаются отдельные значения признака, которые он принимает в вариационном ряду, т. е. конкретное значение варьирующего признака.
Частота ( ) показывает, сколько раз встречается то или иное значение признака. Сумма всех частот – объем выборки: i N .
Иногда также вычисляют частости – частоты, выраженные в долях единицы или в процентах к
11

итогу. Соответственно сумма частостей равна 1 или 100%. Вычисляется по формуле: w |
i |
. |
|
||
i |
i |
|
Накопленные частоты (накопленные частости) – это сумма предыдущих частот (частостей).
В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды.
дискретный вариационный ряд
Характеризует распределение единиц совокупности по порядковому признаку, величина которого принимает только целые значения.
Построим дискретный вариационный ряд на примере данных Табл. 3.
Табл. 3. Данные о тарифных разрядах 50 рабочих одного из цехов завода
3 |
5 |
6 |
3 |
2 |
4 |
3 |
5 |
5 |
5 |
4 |
3 |
2 |
3 |
4 |
5 |
4 |
2 |
4 |
4 |
5 |
3 |
4 |
5 |
4 |
3 |
3 |
6 |
2 |
2 |
4 |
6 |
3 |
4 |
4 |
5 |
4 |
5 |
3 |
3 |
2 |
6 |
3 |
4 |
5 |
3 |
4 |
4 |
5 |
5 |
Для того, чтобы показать распределение рабочих по тарифному разряду, построим вариационный ряд (Табл. 4).
Табл. 4. Дискретный вариационный ряд
Тарифный разряд (варианта xi ) Численность рабочих (частота i )
2 |
6 |
3 |
13 |
4 |
15 |
5 |
12 |
6 |
4 |
Всего: |
50 |
Для визуализации ряда используется столбчатый график (Рис. 4).
Количество рабочих
16
14
12
10
8
6
4
2
0
2 |
3 |
4 |
5 |
6 |
Тарифный разряд
Рис. 4. Столбчатый график
интервальный вариационный ряд
Характеризует распределение единиц совокупности по количественному признаку, величина которого может принимать в определенных пределах любые значения, отличающиеся друг от друга на сколь угодно малую величину.
После определения исследуемого признака, необходимо решить вопрос о количестве групп (интервалов), на которые надо разбить выборку.
12
Для определения оптимального числа групп используется формула Стерджесса: n 1 3,322 lgN , где п – число групп, N – объем выборки. Наличие «пустых» интервалов, в которые не попала ни одна из единиц выборки, свидетельствует о том, что группировка построена неправильно.
После определения числа групп необходимо определить интервалы группировки. Интервал – это значения варьирующего признака, лежащие в определенных границах. Каждый интервал имеет верхнюю и нижнюю границы и свою величину (разность между верхней и нижней границами). Чаще всего строят группировку с равными интервалами. Длина интервала вычисляется по фор-
муле: h |
R |
, где R x |
x |
|
- размах выборки, x |
max |
,x |
min |
- максимальное и минимальное зна- |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
n 1 |
|
|
max |
|
|
|
min |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
чения признака. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Первый интервал группировки обычно xmin |
h |
;xmin |
|
h |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Построим вариационный ряд по данным Табл. 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Табл. 5. Данные об объемах продаж колбасы по месяцам, млн. р. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
9,4 |
|
8,0 |
|
|
|
|
6,3 |
|
10,0 |
15,0 |
|
8,2 |
|
|
|
7,3 |
|
9,2 |
|
5,8 |
|
8,7 |
|
|
|||||||||||
|
|
|
|
5,2 |
|
13,2 |
|
|
|
|
8,1 |
|
7,5 |
11,8 |
|
14,6 |
|
|
8,5 |
|
7,8 |
|
10,5 |
|
6,0 |
|
|
|||||||||||
|
|
|
|
5,1 |
|
6,8 |
|
|
|
|
8,3 |
|
7,7 |
7,9 |
|
9,0 |
|
|
|
10,1 |
|
8,0 |
|
12,0 |
|
14,0 |
|
|
||||||||||
|
|
|
|
8,2 |
|
9,8 |
|
|
13,5 |
|
12,4 |
5,5 |
|
7,9 |
|
|
|
9,2 |
|
10,8 |
|
12,1 |
|
12,4 |
|
|
||||||||||||
|
|
|
|
12,9 |
|
12,6 |
|
|
|
|
6,7 |
|
9,7 |
8,3 |
|
10,8 |
|
|
15,0 |
|
7,0 |
|
13,0 |
|
9,5 |
|
|
|||||||||||
Число интервалов группировки: n 1 3,322 lgN 1 3,322 lg50 6,64 7. |
|
|
|
|
||||||||||||||||||||||||||||||||||
Длина интервала: h |
|
R |
|
15 5,1 |
1,65 1,7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
n 1 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вариационный ряд представлен в Табл. 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Табл. 6. Интервальный вариационный ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
№ |
|
|
Интервалы |
|
|
|
Середина |
|
|
|
|
|
Накопленные |
|
|
|
|
|
Накопленные |
|
|||||||||||||||||
|
|
нижняя |
верхняя |
|
|
Частоты |
|
Частости |
|
|
||||||||||||||||||||||||||||
|
инт. |
|
|
интервала |
|
|
|
|
частоты |
|
|
частости |
|
|||||||||||||||||||||||||
|
|
|
граница |
граница |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
4,25 |
|
5,95 |
|
|
|
|
|
5,1 |
|
4 |
|
|
|
|
|
|
4 |
|
|
|
0,08 |
|
|
0,08 |
|
||||||||||
|
2 |
|
5,95 |
|
7,65 |
|
|
|
|
|
6,8 |
|
7 |
|
|
|
|
|
|
11 |
|
|
|
0,14 |
|
|
0,22 |
|
||||||||||
|
3 |
|
7,65 |
|
9,35 |
|
|
|
|
|
8,5 |
|
16 |
|
|
|
|
|
|
27 |
|
|
|
0,32 |
|
|
0,54 |
|
||||||||||
|
4 |
|
9,35 |
|
11,05 |
|
|
|
|
10,2 |
|
9 |
|
|
|
|
|
|
36 |
|
|
|
0,18 |
|
|
0,72 |
|
|||||||||||
|
5 |
|
11,05 |
|
12,75 |
|
|
|
|
11,9 |
|
6 |
|
|
|
|
|
|
42 |
|
|
|
0,12 |
|
|
0,84 |
|
|||||||||||
|
6 |
|
12,75 |
|
14,45 |
|
|
|
|
13,6 |
|
5 |
|
|
|
|
|
|
47 |
|
|
|
0,1 |
|
|
0,94 |
|
|||||||||||
|
7 |
|
14,45 |
|
16,15 |
|
|
|
|
15,3 |
|
3 |
|
|
|
|
|
|
50 |
|
|
|
0,06 |
|
|
1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Всего: |
|
50 |
|
|
|
|
|
|
— |
|
|
|
1 |
|
|
|
— |
|
||||
Для изображения интервального вариационного ряда используется гистограмма. На оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбцов гистограммы должна быть пропорциональна частотам.
Гистограмма для рассмотренного выше примера представлена на Рис. 5.
13
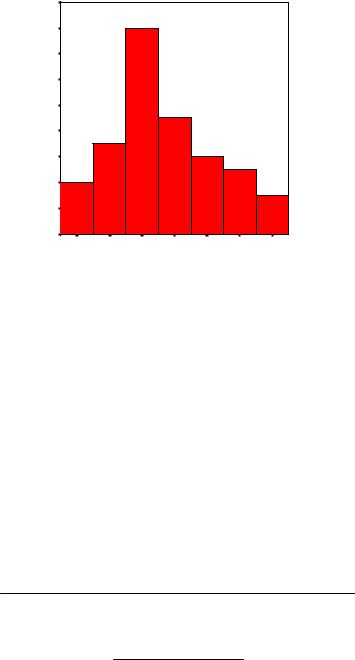
ЧАСТОТА
18
16
14
12
10
8
6
4
2
0
5,1 |
6,8 |
8,5 |
10,2 |
11,9 |
13,6 |
15,3 |
Продажи колбасы, млн.р.
Рис. 5. Гистограмма распределения стоимости основных фондов
СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ
Наиболее распространенной формой статистических показателей является средняя величина, ко-
торая представляет собой обобщенную количественную характеристику признака в выборке в конкретных условиях места и времени. Показатель в форме средней величины выражает типичные черты и дает обобщенную характеристику однотипных явлений по одному из варьирующих признаков.
Значения признака отдельных единиц совокупности могут колебаться в ту или иную сторону под влиянием как основных, так и случайных факторов. Сущность средней заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц выборки, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием основных факторов. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
Определить среднюю во многих случаях можно через исходное соотношение средней (ИСС):
ИСС Суммарное значениеилиобъемосредняемогопризнака .
Числоединицилиобъемсовокупности
Например, для расчета среднего размера вклада в банке, соотношение будет следующим:
ИСС Сумма всехвкладов .
Числовкладов
От того, в каком виде представлены исходные данные для расчета средней, зависит, каким образом будет реализовано ИСС. В каждом конкретном случае для реализации исходного соотношения потребуется одна их форм средней величины:
средняя арифметическая;
средняя гармоническая;
средняя геометрическая;
средняя степенная (квадратическая, кубическая и т. д.)
В каждом конкретном случае в зависимости от характера имеющихся данных существует только одно истинное среднее значение показателя, являющееся следствием реализации ИСС.
Ограничимся рассмотрением лишь средней арифметической.
Свойства средней:
1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на
14

соответствующие им частоты: x i xi i .
2. Сумма отклонений индивидуальных значений признака от средней равна нулю:
xi x i 0.
Средняя арифметическая невзвешенная (простая) используется в тех случаях, когда расчет осуществляется по несгруппированным данным:
|
|
|
|
|
|
|
xi . |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
||
Рассчитаем средний стаж работы по данным Табл. 7. |
|
|
|
|
|
|
|
|
|||||||||||
Табл. 7. Стаж работы рабочих завода |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Табельный номер рабочего |
|
1 |
|
2 |
3 |
4 |
|
5 |
|
6 |
7 |
|||||||
|
Стаж работы (лет) |
|
10 |
|
3 |
5 |
12 |
|
11 |
|
7 |
9 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Воспользуемся следующим исходным соотношением: |
|
|
|
|
|
|
|
|
|||||||||||
|
ИСС |
Совокупныйстажработывсехрабочих |
. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
Числорабочих |
|
|
|
|
|
|
||||||
С учетом имеющихся данных получим: |
|
|
10 3 5 12 11 7 9 |
8,1 года. |
|||||||||||||||
x |
|||||||||||||||||||
|
|||||||||||||||||||
7
Средняя арифметическая взвешенная используется при расчете по сгруппированным данным или вариационным рядам (в случае, когда значения осредняемого признака повторяются):
xxi i .
i
Рассчитаем средний тарифный разряд рабочих по данным Табл. 8.
Табл. 8. Тарифные разряды рабочих завода
Тарифный разряд xi |
2 |
3 |
4 |
5 |
6 |
Число рабочих i |
8 |
16 |
17 |
12 |
7 |
Воспользуемся следующим исходным соотношением: ИСС Совокупный тарифный разряд . Число рабочих
С учетом имеющихся данных получим: x 2 8 3 16 4 17 5 12 6 7 3,9. 8 16 17 12 7
При расчете средней по интервальному вариационному ряду от интервалов переходят к их серединам.
Найдем средние продажи колбасы в месяц по данным Табл. 5.
Табл. 9. Расчетная таблица
№ инт. |
Интервалы |
Середина интервала |
Частота |
xi i |
||
нижняя |
верхняя |
|||||
xi |
i |
|||||
|
граница |
граница |
|
|||
1 |
4,25 |
5,95 |
5,1 |
4 |
20,4 |
|
2 |
5,95 |
7,65 |
6,8 |
7 |
47,6 |
|
3 |
7,65 |
9,35 |
8,5 |
16 |
136,0 |
|
4 |
9,35 |
11,05 |
10,2 |
9 |
91,8 |
|
5 |
11,05 |
12,75 |
11,9 |
6 |
71,4 |
|
6 |
12,75 |
14,45 |
13,6 |
5 |
68,0 |
|
7 |
14,45 |
16,15 |
15,3 |
3 |
45,9 |
|
|
|
|
Всего: |
50 |
481,1 |
|
15

Средние продажи за месяц составили x 481,1 9,62 млн.р 50
СТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ ВАРИАЦИОННОГО РЯДА
МОДА И МЕДИАНА
Мода Mo - это значение изучаемого признака, повторяющееся с наибольшей частотой.
Медиана Me - это значение признака, приходящееся на середину упорядоченной совокупности.
Рассмотрим на примерах способы нахождения моды и медианы.
НАХОЖДЕНИЕ МОДЫ И МЕДИАНЫ ПО НЕСГРУППИРОВАННЫМ ДАННЫМ
Пусть имеются следующие данные о рабочих бригады, состоящей из 9 человек:
Номер рабочего |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Тарифный разряд |
4 |
3 |
4 |
5 |
3 |
3 |
6 |
2 |
6 |
нахождение моды
В данной бригаде больше всего рабочих 3-го разряда, следовательно этот тарифный разряд и будет модальным.
нахождение медианы
Для определения медианы необходимо провести ранжирование:
2 |
3 |
3 |
3 |
4 |
4 |
5 |
6 |
6 |
Центральным в этом упорядоченном ряду является пятое слева значение (рабочий 4-го разряда), следовательно, данное значение признака и будет медианным.
Если ранжированный ряд содержит четное число значений, то медиана определяется как средняя их двух центральных значений.
НАХОЖДЕНИЕ МОДЫ И МЕДИАНЫ ДЛЯ ДИСКРЕТНОГО ВАРИАЦИОННОГО РЯДА
Пусть имеются данные о распределении рабочих предприятия по тарифномуразряду:
Тарифный разряд |
Численность рабочих |
2 |
12 |
3 |
48 |
4 |
56 |
5 |
60 |
6 |
14 |
Всего: |
190 |
нахождение моды
Наибольшую частоту (60 человек) имеет 5-ый тарифный разряд, следовательно, он и является модальным.
нахождение медианы
Для определения медианного значения признака находят номер медианной варианты ряда:
NMe N 1,
2
где N – объем выборки.
Для примера: NMe 190 1 95,5. 2
Полученное дробное значение указывает на то, что медианным интервалом будет тот, в который попали 95-ый и 96-ой рабочие. Для того, чтобы определить этот интервал, необходимо вычислить накопленные частоты:
16

Тарифный разряд |
Численность рабочих |
Накопленные частоты |
2 |
12 |
12 |
3 |
48 |
60 |
4 |
56 |
116 |
5 |
60 |
176 |
6 |
14 |
190 |
Всего: |
190 |
— |
Согласно таблице, 95-ый и 96-ой рабочие находятся в третьей группе, следовательно, медианным является 4-ый разряд.
НАХОЖДЕНИЕ МОДЫ И МЕДИАНЫ ДЛЯ ИНТЕРВАЛЬНОГО ВАРИАЦИОННОГО РЯДА
По данным Табл. 5:
№ |
Интервалы |
Середина |
Частота |
Накопленная |
||
нижняя |
верхняя |
|||||
инт. |
интервала |
i |
частота |
|||
граница |
граница |
xi |
||||
|
|
|
||||
1 |
4,25 |
5,95 |
5,1 |
4 |
4 |
|
2 |
5,95 |
7,65 |
6,8 |
7 |
11 |
|
3 |
7,65 |
9,35 |
8,5 |
16 |
27 |
|
4 |
9,35 |
11,05 |
10,2 |
9 |
36 |
|
5 |
11,05 |
12,75 |
11,9 |
6 |
42 |
|
6 |
12,75 |
14,45 |
13,6 |
5 |
47 |
|
7 |
14,45 |
16,15 |
15,3 |
3 |
50 |
|
|
|
|
Всего: |
50 |
— |
|
нахождение моды
Для интервальных вариационныхрядов мода рассчитывается по формуле:
Mo Mo 1
Mo xMo h Mo Mo 1 Mo Mo 1 ,
где xMo - нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);
h– длина модального интервала;
Mo - частота модального интервала;
Mo 1 - частота интервала, предшествующего модальному;
Mo 1 - частота интервала, следующего за модальным.
Модальным будет 3-ий интервал, так как он имеет наибольшую частоту16.
16 7
Mo 7,65 1,7 16 7 16 9 8,61
нахождение медианы
Медианным будет 3-ий интервал, т.к. его накопленная частота 27 первая превышает половину общей суммы частот 50. Медиана рассчитывается по формуле:
1 |
i SMe 1 |
|||
Me xMe h |
2 |
|||
|
, |
|||
|
|
|||
|
|
Me |
||
где xMe - нижняя граница медианного интервала; h – длина медианного интервала;
SMe 1 - накопленная частота интервала, предшествующего медианному;
17

Me - частота медианного интервала.
1 50 11
Me 7,65 1,7 |
2 |
|
9,14 |
|
16 |
||
|
|
|
КВАРТИЛИ, КВАРТИЛЬНЫЙ РАЗМАХ
Квартили – это значения признака, делящие ранжированную совокупность на четыре равновеликие части.
Различают:
нижнюю квартиль Qн, отделяющую ¼ часть совокупности с наименьшими значениями при-
знака;
среднюю квартиль – медиану;
верхнюю квартиль Qв , отделяющую ¼ часть совокупности с наибольшими значениями при-
знака.
Для расчета квартилей по интервальному вариационномурядуиспользуются формулы:
|
h |
|
1 |
i SQн 1 |
, Q x |
h |
|
3 |
i SQв 1 |
, |
Q x |
4 |
4 |
||||||||
|
|
Q |
|
|
|
|||||
н Qн |
|
|
|
в Qв |
|
|
|
Q |
||
|
|
|
|
н |
|
|
|
|
в |
|
где xQн - нижняя граница интервала, содержащего нижний квартиль (интервал определяется по
накопленной частоте, первой, превышающей 25%);
xQв - нижняя граница интервала, содержащего верхний квартиль (интервал определяется по
накопленной частоте, первой, превышающей 75%); h – длина интервала;
SQн 1 - накопленная частота интервала, предшествующего интервалу, содержащему ниж-
ний квартиль;
SQв 1 - накопленная частота интервала, предшествующего интервалу, содержащему верх-
ний квартиль;
Qн , Qв - частота интервала, содержащего нижний и верхний квартиль соответственно.
Квартильныйразмах – разница между верхней и нижней квартилями: H Qв Qн
Квартильный размахохватывает 50% значений выборки.
Для данных Табл. 5:
№ |
Интервалы |
Середина |
Частота |
Накопленная |
||
нижняя |
верхняя |
|||||
инт. |
интервала |
i |
частота |
|||
граница |
граница |
xi |
||||
|
|
|
||||
1 |
4,25 |
5,95 |
5,1 |
4 |
4 |
|
2 |
5,95 |
7,65 |
6,8 |
7 |
11 |
|
3 |
7,65 |
9,35 |
8,5 |
16 |
27 |
|
4 |
9,35 |
11,05 |
10,2 |
9 |
36 |
|
5 |
11,05 |
12,75 |
11,9 |
6 |
42 |
|
6 |
12,75 |
14,45 |
13,6 |
5 |
47 |
|
7 |
14,45 |
16,15 |
15,3 |
3 |
50 |
|
|
|
|
Всего: |
50 |
— |
|
Интервал, содержащий нижнюю квартиль – 3-ий, т.к. накопленная частота (27) первая превышает ¼ общей сумы частот (12,5).
Интервал, содержащий верхнюю квартиль – 5-ый, т.к. накопленная частота (42) первая превышает
18

¾ общей сумы частот (37,5).
1 |
50 11 |
3 |
50 36 |
|||||
Q 7,65 1,7 |
4 |
7,81; Q 11,05 1,7 |
4 |
|||||
|
|
|
11,48. |
|||||
|
|
|
|
|
||||
н |
16 |
|
в |
6 |
|
|||
|
|
|
|
|
|
|||
Квартильный размах– полоса, шириной 11,48 7,81 3,67 содержит 50% значений выборки.
ПОКАЗАТЕЛИ ВАРИАЦИИ
Исследование вариации имеет важное значение, так как величина вариации признака в статистической совокупности характеризует ее однородность.
В статистической практике для изучения и измерения вариации используются различные показатели (меры) вариации в зависимости от поставленных перед исследователем задач. К ним относятся:
размах вариации R (разность между максимальным и минимальным значением выборки, рассматривали ранее)
стандартное (среднее квадратическое) отклонение
дисперсия
моменты распределения
При изучении вопроса о вариации нужно четко представлять себе условия, порождающие вариацию признаков, а также сущность и значение измерения вариации признаков. Изучение вариации признаков общественных явлений находится в прямой связи с рядами распределения.
СТАНДАРТНОЕ (СРЕДНЕЕ КВАДРАТИЧЕСКОЕ) ОТКЛОНЕНИЕ
Стандартное отклонение оценивает разброс наблюдаемых значений вокруг их средней.
Вычисляется по формулам:
xi x 2
невзвешенное: 
 ;
;
|
|
|
N |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
2 |
i |
||
|
x |
|||||||
|
взвешенное: |
|
|
. |
||||
i |
|
|||||||
|
|
|
|
|
|
|||
Выражается в тех же единицах измерения, что и количественный признак.
В пределах x находится 68,3% вариант. Более того, в пределах x 2 - 95,4% вариант, в пре-
делах x 3 - 99,7%. На практике почти не встречаются отклонения, которые превышают 3 . Отклонение 3 может считаться максимально возможным. Это положение называется правилом «трех сигм»*. Таким образом, по показателю можно оценить полосу, в которой происходит вариация «основной массы» (95,4%) значений признака. Как правило, в оставшиеся 5% входят выбросы – нетипичные значения.
Оценим разброс значений по данным Табл. 5.
№ |
Интервалы |
Середина |
Частота |
|
|
|
2 |
|
|
|
2 |
|
||
нижняя |
верхняя |
интервала |
xi x |
xi x |
i |
|||||||||
инт. |
i |
|
|
|||||||||||
граница |
граница |
xi |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
4,25 |
5,95 |
5,1 |
4 |
20,43 |
|
81,72 |
|
||||||
2 |
5,95 |
7,65 |
6,8 |
7 |
7,95 |
|
55,67 |
|
||||||
3 |
7,65 |
9,35 |
8,5 |
16 |
1,25 |
|
20,07 |
|
||||||
4 |
9,35 |
11,05 |
10,2 |
9 |
0,34 |
|
3,03 |
|
||||||
* Правило «трех сигм» имеет место в условиях нормального распределения, которое будет рассмотрено позже.
19

|
|
|
|
|
№ |
|
|
|
|
Интервалы |
|
Середина |
Частота |
|
|
|
|
2 |
|
|
|
2 |
|
|
|||||
|
|
нижняя |
верхняя |
|
интервала |
xi |
x |
xi x |
i |
|
|||||||||||||||||||
|
|
|
|
инт. |
|
|
|
i |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
граница |
граница |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
11,05 |
|
|
12,75 |
|
11,9 |
6 |
5,20 |
|
31,19 |
|
|
|||||||||||
|
|
|
|
6 |
|
|
12,75 |
|
|
14,45 |
|
13,6 |
5 |
15,84 |
|
79,20 |
|
|
|||||||||||
|
|
|
|
7 |
|
|
14,45 |
|
|
16,15 |
|
15,3 |
3 |
32,26 |
|
96,79 |
|
|
|||||||||||
|
|
|
|
Сумма: |
|
|
|
— |
— |
|
— |
50 |
|
— |
|
367,67 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
xi |
|
2 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
367,67 |
|
|
2,71 лет, т.е. 95% продаж |
варьируются |
|
в интервале |
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
i |
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 9,42 2 2,71, т.е. от 6,71 до 12,13 млн.р. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
При небольшом объеме выборки N 30 |
стандартное отклонение можно рассчитывать по фор- |
||||||||||||||||||||||||||||
муле 
 x2 x 2 , которая вытекает из приведенных выше (если возвести правую часть равенства в квадрат и почленно разделить на N i ).
x2 x 2 , которая вытекает из приведенных выше (если возвести правую часть равенства в квадрат и почленно разделить на N i ).
ДИСПЕРСИЯ
Представляет собой стандартное отклонение в квадрате.
невзвешенная: 2 xi x 2 ;
N
взвешенная: 2 xi x 2 i .
i
Дисперсия обладает одним существенным недостатком: ее значение выражается в квадратных единицах. Но, несмотря на это, она обладает рядом замечательных свойств, использование которых получило широкое распространение в различных областях знаний, на их основе были разработаны новые методы исследования, а также новые показатели количественной характеристики большого класса явлений.
Свойства дисперсии:
1.Дисперсия постоянной величины равна нулю.
2.Уменьшение всех значений признака на одну и ту же величину а не меняет величины дисперсии:
(2x a) x2 .
Значит, средний квадрат отклонений можно вычислить не по заданным значениям признака, а по отклонениям их от какого-либо постоянного числа.
3.Уменьшение всех значений признака в k раз уменьшает дисперсию в k2 раз:
2x/k k2x2 .
4.Дисперсия (разброс) от средней всегда меньше дисперсий, вычисленных от любых других величин.
20
