3.4 Похідні та диференціали вищих порядків

(higher derivative, higher-order differential)

 

Нехай функція  диференційовна на проміжку X, а  - її похідна, яка також є функцією відносно x. Від цієї функції знову можна шукати похідну за умови, що вона існує на заданому проміжку. Похідна від похідної  називається похідною другого порядку (second-order derivative) функції  і позначається одним із символів:

 

.

 

Так у фізиці, якщо  - закон, за яким змінюється пройдений шлях при прямолінійному русі точки, то  є прискоренням (acceleration) цієї точки в момент часу t.

 

Аналогічно  і т. д.

 

Взагалі похідною n-го порядку від функції  називається похідна від похідної -го порядку і позначається

 

, або , або .

 

Зауваження. При , похідну n-го порядку позначають відповідно ; при  позначають:  або .

Приклад 3.17. Знайти похідну другого порядку від функції

 

.

Розв’язання. Знаходимо спочатку  за формулою .

 

 

.

 

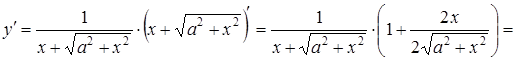
Знаходимо похідну від отриманої функції:

 

 

, тобто .

 

 

Приклад 3.18. Знайти похідну n-го порядку від функції .

Розв’язання.

.

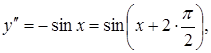
Формула Лейбніца. Якщо функції ,  мають похідні до n-го порядку включно, то для обчислення похідної n-го порядку від добутку цих функцій використовують формулу Лейбніца:

.         (3.14)

 

Похідні вищих порядків від функцій, заданих параметрично. Якщо функції  і  параметрично задають функцію , то похідні , , можна послідовно обчислити за формулами:

 

,  і т. д.

 

Так, для похідної другого порядку має місце формула:

 

.                               (3.15)

 

Приклад 3.19. Знайти похідну  функції , заданої параметрично: , .

Розв’язання.

 

.

 

за формулою (3.15)

 

.

 

Диференціали вищих порядків. Нехай функція  диференційовна на проміжку X. Її диференціал

 

 

називається також диференціалом першого порядку і його можна розглядати як функцію змінної x(приріст аргументу  вважається сталим).

Означення 3.4. Диференціалом другого порядку (second differential) функції  в точці xназивається диференціал від її диференціала першого порядку (за умови, що повторний приріст незалежної змінної x збігається з попереднім ) і позначається :

 

.

 

За означенням маємо

 

,

 

позначають . Таким чином

 

.                                     (3.16)

 

Аналогічно, диференціалом n-го порядку (позначається ), n=2,3,... називається диференціал від диференціала порядку  за умови, що в диференціалах весь час беруться одні й ті самі прирости  незалежної змінної x. Тобто

 

.

 

При цьому справедлива формула:

 

.                                     (3.17)

 

 

Приклад 3.20. Обчислити , якщо .

Розв’язання. Скористаємось формулою (3.16). Для цього знайдемо :

, .

 

Отже

.