2.2 Основные точки и линии снимка

ЦЕНТРАЛЬНАЯ ПРОЕКЦИЯ КАК ГЕОМЕТРИЧЕСКАЯ ОСНОВА АЭРОФОТОСНИМКА

Под проекцией следует понимать изображение пространственных фигур на плоскости или какой-либо другой поверхности.

В ортогональной проекции все точки фигуры проектируются на горизонтальную плоскость по прямым линиям, перпендикулярным этой плоскости. Эти прямые линии являются в данном случае отвесными линиями.

Центральная проекция получается в результате проектирования всех точек фигуры на какую-либо плоскость или поверхность по прямым линиям. выходящим из определенной точки S, называемой центром проекции (рис. 14, (рис.15).

Рис. 14. Центральная проекция (наклонный аэрофотоснимок)

При центральном проектировании используются следующие основные плоскости, линии и точки:

Е – горизонтальная плоскость, проходящая через какую-либо точку местности и называемая плоскостью основания. Её еще называют предметной плоскостью;

Р – картинная плоскость (аэрофотоснимок). На этой плоскости размещается центральная проекция объектов предметной плоскости;

W – плоскость главного вертикала (направления съёмки);

SoO – главный луч;

So-f – фокусное расстояние объектива фотокамеры;

Н – высота съёмки – расстояние центра проекции относительно основания;

о – главная точка аэрофотоснимка;

О – проекция главной точки на предметную плоскость;

с – точка нулевых искажений. В этой точке горизонтальные углы не искажаются;

С – проекция точки нулевых искажений на предметную плоскость;

n – точка надира (пересечения отвесной линии, проходящей через центр проекции, с плоскостью снимка);

ТТ – ось перспективы (линия основания);

hh – главная горизонталь;

Рис. 15. Центральная проекция (горизонтальный аэрофотоснимок)

V_i –главная вертикаль;

h₁h_i – линия действительного горизонта;

i – точка схода картинной плоскости;

V – главная точка оси перспективы (пересечения линии основания с главной вертикалью).

Различают элементы внутреннего ориентирования аэрофотоснимка и элементы внешнего ориентирования. К элементам внутреннего ориентирования относятся фокусное расстояние f и координаты х_о, у₀ главной точки в системе координат снимка оху. а к элементам внешнего (рис. 3) – координаты Х_s, Y_s, Z_s точки фотографирования S в системе координат OXYZ местности, а также углы Эйлера:  – угол поворота снимка в плоскости XY,  – угол продольного наклона снимка в плоскости ZX,  – угол поперечного наклона в плоскости ZY.

В частном случае, рассматриваемом в настоящей работе (см. рис. 14), =0 и =0, Za =H, а зависимость между координатами точки на снимке и на местности определяется формулами:

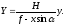(1)

2.3 Масштабы арофотоснимка

Будем полагать аэроснимок горизонтальный. Тогда, если местность представляет собой горизонтальную плоскость, масштаб аэрофотоснимка определится в зависимости от высоты полета летательного аппарата Н и фокусного расстояния АФА f_% получают аэрофотоснимки различных масштабов. Отношение длины отрезка на аэрофотоснимке ab к длине того же отрезка на местности А В называется численным масштабом аэрофотоснимка. Как следует из рис. 16, масштаб аэрофотоснимка можно определить по формуле:

(2)

где m – знаменатель масштаба АФС.

Но поскольку

(3)

то

(4)

Из формулы (3) можно вычислить высоту фотографирования:

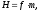(5)

если известен ее масштаб и фокусное расстояние фотокамеры.

Рис. 16 Схема определения масштаба аэрофотоснимка

При наклонном положение оптической оси АФА, а также при пересеченном или горном рельефе снимаемой местности масштабы аэрофотоснимков для разных их частей будут неодинаковы. В частности при отклонении оптической оси АФА от отвесной линии на угол αo масштаб аэрофотоснимка в разных его точках можно определять по формуле:

(6)

При пересеченном и горном рельефах местности масштабы аэрофотоснимков будут переменными также в связи с искажениями из-за рельефа. Как следует из рис. 17. если точка А имеет превышение (+h) и точка В (-h) относительно условного (среднего) горизонта, а точки А₀ и В_с — их ортогональные проекции, то точки a₀, а и b₀, b являют ся соответственно центральными проекциями этих точек на аэрофотоснимке Р. В этом случае расстояния aa₀=δha и bb₀=δhb являются смешениями точек a и b на аэрофотоснимке за счет соответствующих превышений. Только в одной точке N аэрофотоснимка — точке надира (см. рис. 17), являющейся проекцией отвесной линии, проходящей через центр объектива, искажений из-за рельефа не будет, т.е. δh= 0. Поэтому при рисовке горизонталей и контуров местности в положение соответствующих точек необходимо вводить поправки за рельеф местности δhпо направлению к главной точке при положительном превышении и в обратную сторону — при отрицательном.

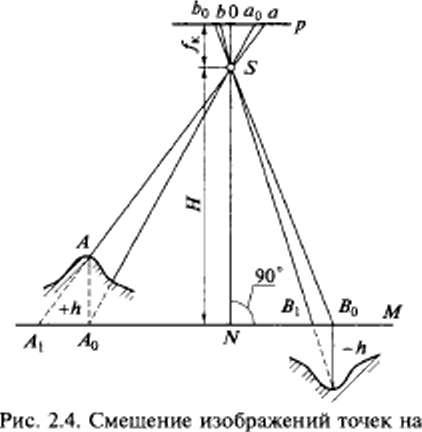
Рис. 17 Смещение изображений точек на аэрофотоснимке в плане из-за рельефа

Ранее было установлено, что масштаб горизонтального снимка равнинной местности постоянен и определяется отношением фокусного расстояния съемочной камеры к высоте фотографирования. Наклонный снимок содержит перспективные искажения, и его масштаб уже не будет постоянным. В частности, из рис. 18 следует, что

для снимка P⁰:; для снимкаP:.

Следовательно, масштаб изображения следует опреде­лять как от­но­шение бес­ко­нечно малых отрезков наклонного снимка и мест­ности:

(7)

где dl иdL– бесконечно малые отрезки снимка и местности, связанные с бесконечно малыми приращениями координат ограничивающих их точек следующими зависимостями (рис. 19):

(8)

Для вывода формулы, определяющей масштаб наклонного снимка по произвольному направлению, используются формулы связи координат точек снимка и местности, при выводе которых координатные оси ox и OX совмещаются с главной вертикалью и ее проекцией.

После преобразований формула масштаба снимка в точке с координатами x, y по произвольному направлению примет вид

, (9)

где

.

Выполним анализ формулы (9), получим формулы масштаба в основных точках снимка по главной вертикали и по горизонталям.

1. Снимок горизонтальный (_с= 0). Подстановка _c дает k = 1, c = 0, и вместо (9) будем иметь

. (10)

Следовательно, масштаб горизонтального снимка плоской местности – величина постоянная, не зависящая от положения точки.

2. Масштаб по главной вертикали (y = 0,  = 0). Подстановка в (9) дает k=cos_c и c=0. Тогда формула масштаба по глав­ной вер­тикали

. (11)

3. Масштаб по горизонталям ( = 90). Подкоренное вы­ра­же­ние в знамена­теле формулы (9) равно k, и искомый масштаб

. (12)

Как видно, масштаб по любой горизонтали является величиной постоянной, что и подтверждает перспектива сетки квадратов.

Действуя аналогично, можно получить формулы для расчета масштаба по главной вертикали и горизонталям в основных точках.

Масштаб в точке нулевых искажений.

Подставив в (9)y=0,oc=x=–f(1–cos)/sin согласно(20),k=1, c=0, получим

. (13)

Масштаб в точке надира(x= – ftg, k=1/cos, c=0):

. (14)

Масштаб в главной точке снимка(x=0, k=cos, c=0):

. (15)

4. Изменение масштаба в пределах аэроснимка можно получить, определив разность масштабов по главной вертикали в двух симметрично расположенных точках с абс­циссами +x и –x:

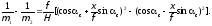
После несложных преобразований, полагая, с достаточной для приближенных оценок точностью, что средний масштаб аэроснимка определяется по формуле (13):

. (16)

Расчеты по этой формуле показывают, что при x=f и _c=30 относительное измене­ние масштаба составит около 1/30. С такой же точностью будут определены и длины измеренных на снимке линий. Следовательно, выполнять измерения по контактным аэроснимкам с использованием их среднего масштаба нужно весьма осторожно.