§ 3. Физические свойства газов Работа
При выводе расчетных формул будет использовано понятие «потенциальная работа».
Потенциальной называется работа перемещения газов из области одного давления р1 в область другого давления р2.
Элементарные величины потенциальной работы соответствуют бесконечно малым изменениям давления:
(7.1)
(7.2)
где δW — элементарная потенциальная работа любого количества газа в Н∙м; V — объем газа в м3; р — давление газа в Па; т — масса газа в кг; v — удельный объем газа в м3/кг.
При перемещении газа в газопроводах распределение потенциальной работы Н. И. Белоконь формулирует следующим образом:
(7.3)
где l* — удельная эффективная работа, передаваемая телам внешней системы (для газопроводов l* = 0); l** — необратимые превращения работы
(7.4)
λ — коэффициент гидравлического сопротивления; w — линейная скорость газа; х — расстояние от начала газопровода до рассматриваемой точки; D— внутренний диаметр газопровода; z — положение рассматриваемой точки газопровода по высоте; g — ускорение силы тяжести.
Из аналитического выражения потенциальной работы следует, что работа затрачивается на преодоление трения газа о стенки газопровода, на изменение положения газа и его линейной скорости.
Уравнение Клапейрона
Уравнение Клапейрона получается путем сопоставления законов Бойля— Мариотта и Гей-Люссака.
По закону Бойля. — Мариотта
откуда удельный объем
Удельный объем идеального газа при температуре 0° С и любом заданном давлении
Подставив это выражение удельного объема v0 в выражение удельного объема этого газа при любой температуре и том же давлении, получим
откуда
Произведем замену
и
где
α0
— температурный коэффициент объемного
расширения идеальных газов при 0° С,
сохраняющий одно и то же значение при
всех давлениях и одинаковый
для
всех идеальных газов (α0
≈
1/
°C).
После подстановки получаем уравнение состояния идеальных газов — уравнение Клапейрона:
(7.5)
где р — абсолютное давление идеального газа в Па; v — удельный объем идеального газа в м3/кг; R — газовая постоянная идеального газа в (Н∙м)/(кг∙К); Т — абсолютная температура газа в К.
Уравнение Клапейрона может быть записано также в виде
где ρ — плотность газа в кг/м.
Если умножить левую и правую части уравнения состояния на количество газа в единицах массы (т), то получим уравнение состояния для любого количества газа
(7.6)
где V — полный объем газа в м3; m — масса газа в кг.
Газовая постоянная R — есть работа расширения единицы количества газа (1 кг) при нагревании его на 1°С (или 1 К) при постоянном давлении (р = idem).
Газовые постоянные некоторых газов:
воздух R = 29,27 (кгс∙м)/(кг∙К) = 287,04 (Н∙м)/(кг∙К);
метан (СН4) R = 52,95 (кгс ∙ м)/(кг ∙ К) = 519,26 (Н∙м)/(кг∙К);
пропан (С3Н8) R = 19,93 (кгс∙м)/(кг∙К) = 195,45 (Н∙м)/(кг∙К);
н-бутан (С4Н10) R = 14,59 (кгс∙м)/(кг∙К) = 143,08 (Н∙м)/(кг∙К).
Параметры физического состояния реальных газов — температура 0° С и давление 760 мм рт. ст. — далеки от условий идеального состояния.
Для реальных газов составлено большое число уравнений состояния. Наиболее распространенное — уравнение Клапейрона с поправочным коэффициентом:
(7.7)
где Z — коэффициент, учитывающий отклонение реальных газов от законов идеальных газов. Коэффициент Ъ часто называют коэффициентом сжимаемости.
Величины коэффициента отклонения обычно определяются по графикам (рис. 7.1), в которых коэффициент Z приводится в зависимости от приведенных параметров (давление и температура) газа:
(7.8)
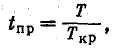(7.9)
где рпр — приведенное давление; р — абсолютное давление газа; pкр — критическое давление газа; tпр — приведенная температура; Т — абсолютная температура газа; Tкр — критическая температура газа.
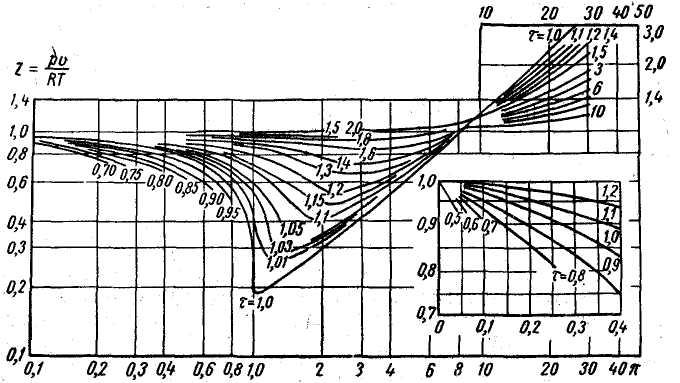
Рис. 7.1. График зависимости коэффициента сжимаемости газов от приведенного давления и приведенной температуры.
Критическим давлением называется такое давление, при котором и выше которого нельзя испарить жидкость ни при каком повышении температуры.
Критическая температура — это температура, при которой и выше которой ни при каком повышении давления нельзя сконденсировать пар.
Значения критических параметров некоторых газов приведены в табл. 7.1.
Таблица 7.1