
Физика / Физика / Механика. Лекции / lekcii_meh / glava1
.pdf
имеют определенной точки приложения: они могут откладываться от любой точ-
ки оси вращения.
Угловой скоростью называется векторная величина, равная первой произ-
водной угла поворота тела по времени:
R |
ϕ |
|
dϕ |
|
|
|
|
R |
|
ω = lim |
|
= |
|
. |
|
|
|||
t→0 |
t |
|
dt |
|
Вектор ω направлен вдоль оси вращения по правилу правого винта, т.е. так же как и вектор dϕ (рис. 7).
Единица измерения угловой скорости:
[ω]= рад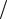 с.
с.
Линейная скорость точки (рис. 6)
v = lim Ds = lim R × Dj = R lim Dj = Rω, |
|
t→0 t t→0 t |
t→0 t |
т.е. v = Rω.
В векторном виде формулу для линейной скорости можно написать как век-
торное произведение:
R = ωR ×
v [ R].
Если ω = const , то вращение равномерное и его можно характеризовать пе-
риодом вращения Т – временем, за которое точка совершит один полный оборот
T = 2ωπ .
Число полных оборотов, совершаемых телом при равномерном его движе-
нии по окружности, в единицу времени называется частотой вращения:
n = 1 = ω ,
T 2π
ω = 2πn .
Угловым ускорением называется векторная величина, равная первой про-
изводной угловой скорости по времени:
R dωR
ε = .
dt
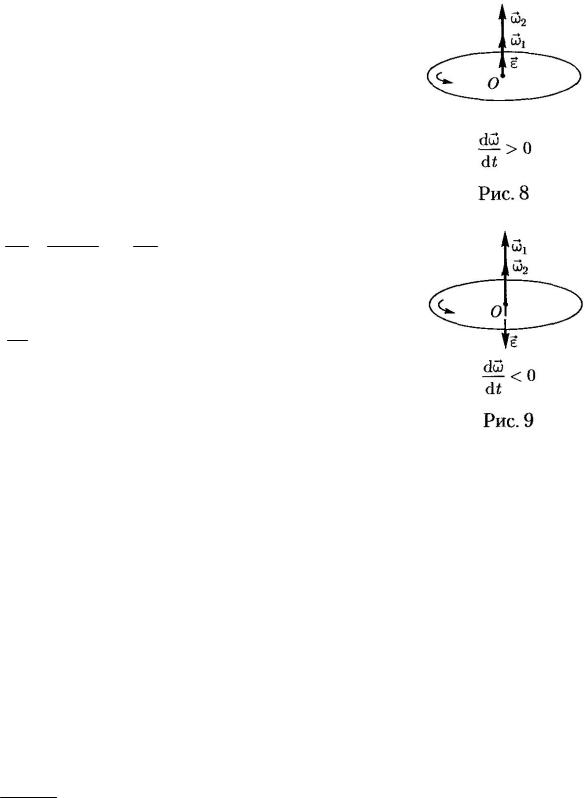
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω (рис. 8), при замедленном – противонаправлен ему (рис. 9).
Тангенциальная составляющая ускорения
aτ = dv = d(ωR) = R dω = Rε . dt dt dt
Нормальная составляющая ускорения
an = v2 = ω2R2 = ω2R .
RR
Связь между линейными и угловыми величинами выражается следующими формулами:
s = Rϕ, v = Rω, aτ = Rε, an = ω2R.
Вслучае равнопеременного движения точки по окружности (ε = const)
ω= ω0 ± εt , ϕ = ω0t ± εt2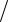 2 , где ω0 – начальная угловая скорость.
2 , где ω0 – начальная угловая скорость.
Задача 1. Материальная точка движется по окружности радиусом R = 0,1 м с постоянным по величине угловым ускорением ε = 0,5 с–2 . Определите: а) полное линейное ускорение a точки через 2 с после начала вращения; б) ее нормальное ускорение an через один оборот; в) угол между вектором полного ускорения и радиусом окружности в указанные моменты времени.
Решение. Полное ускорение точки определяется выражением a = 
 aτ2 + an2 ,
aτ2 + an2 ,
где aτ = εR – тангенциальное ускорение, an = ω2R – нормальное ускорение точ-
ки. В формуле для нормального ускорения заменим угловую скорость выражени-

ем ω = εt , в результате получим an = ε2t2R . Тогда выражение для полного уско-
рения будет иметь вид
a = 
 ε2R2 + ε4t4R2 = εR
ε2R2 + ε4t4R2 = εR
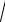 1+ ε2t4 .
1+ ε2t4 .
Подставив числовые значения, получим
a = 0,5 ×0,1× 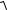
 1+ 0,52 × 24 = 0,11 м/с2 .
1+ 0,52 × 24 = 0,11 м/с2 .
Угол, на который поворачивается материальная точка при вращении по ок-
ружности с постоянной угловой скоростью можно определить по формуле
j = et2 = w2 . 2 2e
Отсюда выразим квадрат угловой скорости w2 = 2ej и подставим в формулу для нормального ускорения.
an = 2εϕR
При повороте точки на один оборот угол равен ϕ = 2π. Подставим числовые зна-
чения и вычислим нормальное ускорение
an = 2 ×0,5 × 2 ×3,14 ×0,1 = 0,63 м/с2 .
Как видно из рисунка, угол между вектором полного ускорения и радиусом
окружности через один оборот можно определить по формуле
tga = |
aτ |
= |
εR |
= |
1 |
= |
1 |
= 0,08 или α ≈ 4,5° |
|
2ejR |
2j |
2 × 2 ×3,14 |
|||||
|
an |
|
|
|
||||
Задача 2. Закон вращения диска радиусом R = 0,1 м вокруг неподвижной оси имеет вид j =10 + 5t2 - 2t4 . Найдите величину и направление ускорения точки,
находящейся на ободе диска, спустя t =1 с после начала движения.
Решение. Проекцию вектора угловой скорости диска на ось вращения Z оп-
ределим по формуле
wZ = dϕ = 10t - 8t3 dt
или для момента времени t =1 с получим
wZ = 10 ×1- 8 ×13 = 2 рад/с,
т.е. угловая скорость направлена вдоль оси Z и равна по величине ω = 2 рад/с.
Нормальное ускорение точки на ободе диска определим по формуле an = w2R или an = 22 ×0,1 = 0,4 м/с2 .
Проекция углового ускорения диска на ось Z определяется выражением
eZ = dωZ = 10 - 24t2 . dt
Подставим числовые значения
eZ =10 - 24 ×12 = -14 рад/с2 .
Угловое ускорение направлено против оси Z и равно по величине e = 14 рад/с2 .
Тангенциальное ускорение определим из выражения
aτ = εZR,
подставив числовые значения aτ = (-14) ×0,1 = -1,4 м/с2 .
Знак минус говорит о том, что тангенциальная составляющая ускорения точки aτ
направлена против вектора скорости v.
Тогда, как это видно из рисунка, полное ускорение равно
a = 
 aτ2 + an2 или после подстановки числовых значений получим a =
aτ2 + an2 или после подстановки числовых значений получим a = 
 (-1,4)2 + 0,42 = 1,46 м/с2 .
(-1,4)2 + 0,42 = 1,46 м/с2 .
Задача 3. Угловая скорость вращающегося тела изменяется по |
закону |
||||
w = 2t + 3t2 |
(рад/с). На какой угол повернулось тело за время от t =1с до t |
2 |
= 3 с? |
||
|
|
1 |
|
||
Решение. Для определения угла, на который повернется тело за указанный |
|||||
промежуток времени, воспользуемся формулой |
|
|
|||
t2 |
3 |
|
3 |
|
|
j = ∫wdt = ∫(2t + 3t2 )dt = (t2 + t3 ) |
|
|
|
||
|
1 = 34 рад . |
|
|
||
|
|
|
|||
t1 |
1 |
|
|
|
|
