книги бурение / Теория и опыт добычи газа / 1

䂇‰ ‡Ú Ò Â‰ÌÂÈ ÒÍÓ ÓÒÚË c2 Б‡ПВМВМ ‚˚ ‡КВМЛВП a2T, „‰Â a – НУ˝ЩЩЛˆЛВМЪ Ф УФУ ˆЛУМ‡О¸МУТЪЛ.

ê‡Á‰ÂÎË‚ (1.8) ̇ (1.9), ÔÓÎÛ˜ËÏ Á‡ÍÓÌ ÉÂÈ-ã˛Ò͇҇

Ъ.В. У·˙ВП˚ „‡Б‡ Ф Л ФУТЪУflММУП ‰‡‚ОВМЛЛ УЪМУТflЪТfl Н‡Н Лı ‡·ТУО˛ЪМ˚В ЪВПФВ ‡ЪЫ ˚.

á‡ÍÓÌ ò‡ Îfl

ЦТОЛ М‡„ ВЪ¸ „‡Б Ф Л ФУТЪУflММУП У·˙ВПВ УЪ ЪВПФВ ‡ЪЫ ˚ T1 ‰У ЪВПФВ ‡ЪЫ ˚ T2, ЪУ УТМУ‚МУВ Ы ‡‚МВМЛВ ‰Оfl ФВ ‚У„У ТУТЪУflМЛfl

Ъ.В. Ф Л ФУТЪУflММУП У·˙ВПВ ‰‡‚ОВМЛfl „‡Б‡ УЪМУТflЪТfl Н‡Н Лı ‡·ТУО˛ЪМ˚В ЪВПФВ ‡ЪЫ ˚.

á‡ÍÓÌ Ä‚Ó„‡‰ Ó

з‡ФЛ¯ВП УТМУ‚МУВ Ы ‡‚МВМЛВ ‰Оfl ‰‚Ыı „‡БУ‚, Б‡МЛП‡˛˘Лı У‰ЛМ‡НУ‚˚В У·˙ВП˚ Ф Л У‰ЛМ‡НУ‚˚ı ЪВПФВ ‡ЪЫ ‡ı Л ‰‡‚ОВМЛflı; ‰Оfl ФВ ‚У„У „‡Б‡

‰Îfl ‚ÚÓ Ó„Ó „‡Á‡

и Л ‡‚Мfl‚ Ф ‡‚˚В ˜‡ТЪЛ (1.12) Л (1.13) Л ТУН ‡˘‡fl ˜ЛТОУ‚˚В НУ˝ЩЩЛˆЛВМЪ˚ Л ‚˚ ‡КВМЛfl НЛМВЪЛ˜ВТНУИ ˝МВ „ЛЛ ПУОВНЫО, НУЪУ ˚В ‡‚М˚ ‚‚Л‰Ы ‡‚ВМТЪ‚‡ ЪВПФВ ‡ЪЫ , ФУОЫ- ˜‡ВП

З У‰ЛМ‡НУ‚˚ı У·˙ВП‡ı Ф Л У‰ЛМ‡НУ‚˚ı ЪВПФВ ‡ЪЫ ‡ı Л ‰‡‚ОВМЛflı ТУ‰В К‡ЪТfl У‰ЛМ‡НУ‚˚В НУОЛ˜ВТЪ‚‡ ПУОВНЫО.

уЛТОУ ПУОВНЫО ‚ У·˙ВПВ У‰МУИ „ ‡ПП-ПУОВНЫО˚ М‡Б˚‚‡ВЪТfl ˜ЛТОУП Д‚У„‡‰ У Л У·УБМ‡˜‡ВЪТfl N. á̇˜ÂÌË N ‡‚ÌÓ 6,023 1023 ПУОВНЫО.

й·˙В‰ЛМВММ˚И Б‡НУМ е‡ ЛУЪЪ‡ – ЙВИ-г˛ТТ‡Н‡

з‡ФЛ¯ВП УТМУ‚М˚В Ы ‡‚МВМЛfl ‰Оfl ‰‚Ыı ТУТЪУflМЛИ „‡Б‡ Ф Л ЛБПВМВМЛЛ У·˙ВП‡, ‰‡‚ОВМЛfl Л ЪВПФВ ‡ЪЫ ˚:

и УЛБ‚В‰ВМЛВ У·˙ВП‡ „‡Б‡ М‡ ‰‡‚ОВМЛВ, ‰ВОВММУВ М‡ ‡·ТУ- О˛ЪМЫ˛ ЪВПФВ ‡ЪЫ Ы, ‰Оfl ‰‡ММУИ П‡ТТ˚ „‡Б‡ ВТЪ¸ ‚ВОЛ˜ЛМ‡ ФУТЪУflММ‡fl.

д‡Н ‚Л‰ЛП, ЛБ УТМУ‚МУ„У Ы ‡‚МВМЛfl НЛМВЪЛ˜ВТНУИ ЪВУ ЛЛ ˜ ВБ‚˚˜‡ИМУ Ф УТЪУ ФУОЫ˜‡˛ЪТfl ‚ТВ „‡БУ‚˚В Б‡НУМ˚, ‡МВВ ЫТЪ‡МУ‚ОВММ˚В УФ˚ЪМ˚П ФЫЪВП.

1.2.3.мкДЗзЦзаЦ лйлнйьзаь аСЦДгъзхп ЙДбйЗ

àЙДбйЗДь ийлнйьззДь

м ‡‚МВМЛВП ТУТЪУflМЛfl М‡Б˚‚‡ВЪТfl Ы ‡‚МВМЛВ, Т‚flБ˚‚‡˛- ˘ВВ УТМУ‚М˚В Ф‡ ‡ПВЪ ˚, ı‡ ‡НЪВ ЛБЫ˛˘ЛВ ТУТЪУflМЛВ „‡Б‡: У·˙ВП, ‰‡‚ОВМЛВ Л ЪВПФВ ‡ЪЫ Ы. м ‡‚МВМЛВ ТУТЪУflМЛfl Л‰В‡О¸-

32

М˚ı „‡БУ‚, ЛОЛ Ы ‡‚МВМЛВ дО‡ФВИ УМ‡ – еВМ‰ВОВВ‚‡, ПУКВЪ ·˚Ъ¸ ФУОЫ˜ВМУ ЛБ У·˙В‰ЛМВММУ„У Б‡НУМ‡ е‡ ЛУЪЪ‡ – ЙВИ- г˛ТТ‡Н‡ (1.15).

З Ф ‡‚УИ ˜‡ТЪЛ Ы ‡‚МВМЛfl (1.15) ‚ПВТЪУ ЛМ‰ВНТ‡ “2” ФУТЪ‡- ‚ЛП МЫОВ‚˚В ЛМ‰ВНТ˚, ‚ ОВ‚УИ ˜‡ТЪЛ ЛМ‰ВНТ˚ МВ ·Ы‰ВП ФЛ- Т‡Ъ¸, Ъ‡Н Н‡Н ОВ‚‡fl ˜‡ТЪ¸ ПУКВЪ УЪМУТЛЪТfl Н О˛·УПЫ ТУТЪУflМЛ˛:

ЦТОЛ ˝ЪУ Ы ‡‚МВМЛВ ФЛТ‡Ъ¸ ‰Оfl В‰ЛМЛˆ˚ П‡ТТ˚ УФ В‰ВОВММУ„У „‡Б‡, ЪУ Ф ‡‚‡fl ˜‡ТЪ¸ ·Ы‰ВЪ ‚ВОЛ˜ЛМУИ ФУТЪУflММУИ, НУЪУ-Ы˛ М‡Б˚‚‡˛Ъ Ы‰ВО¸МУИ „‡БУ‚УИ ФУТЪУflММУИ Л У·УБМ‡˜‡˛Ъ B. нУ„‰‡ Ы ‡‚МВМЛВ (1.16) Б‡ФЛ¯ВЪТfl ‚ ‚Л‰В

щЪУ Ы ‡‚МВМЛВ ‚ФВ ‚˚В ·˚ОУ ФУОЫ˜ВМУ дО‡ФВИ УМУП. СОfl П‡ТТ˚ m „ ‡ППУ‚ ‰‡ММУ„У „‡Б‡ УМУ ЛПВВЪ ‚Л‰

pV = mBT.

й‰М‡НУ Ы‰У·МВВ Ы ‡‚МВМЛ˛ ТУТЪУflМЛfl Л‰В‡О¸М˚ı „‡БУ‚ Ф Л‰‡Ъ¸ ·УОВВ ЫМЛ‚В Т‡О¸М˚И ‚Л‰, ˜ЪУ Л ·˚ОУ Т‰ВО‡МУ С.а. еВМ‰ВОВВ‚˚П ТОВ‰Ы˛˘ЛП У· ‡БУП. м ‡‚МВМЛВ (1.17) ФВ-ВФЛТ˚‚‡ВЪТfl ‰Оfl У‰МУ„У ПУОfl „‡Б‡. иУТНУО¸НЫ У‰ЛМ ПУО¸ О˛-

·˚ı „‡БУ‚ Ф Л МУ П‡О¸МУП ‰‡‚ОВМЛЛ p0 Á‡ÌËχÂÚ Ó·˙ÂÏ VÓ· = 22,41 Î, ÚÓ Ô ‡‚‡fl ˜‡ÒÚ¸ (1.17) ·Û‰ÂÚ ÛÌ˂ ҇θÌÓÈ „‡ÁÓ‚ÓÈ

ФУТЪУflММУИ ‰Оfl ‚ТВı „‡БУ‚; У·УБМ‡˜Л‚ ВВ R, ‚ПВТЪУ (1.17) ФУОЫ˜ЛП

ÖÒÎË Ê ‡ÒÒÏ‡Ú Ë‚‡ÂÚÒfl Ô ÓËÁ‚ÓθÌÓ ÍÓ΢ÂÒÚ‚Ó „‡Á‡, Ì‡Ô ËÏ m, Л ВТОЛ ПУОВНЫОfl М‡fl П‡ТТ‡ µ, ЪУ ˜ЛТОУ ПУОВИ‡‚МУ m/µ Л Ы ‡‚МВМЛВ дО‡ФВИ УМ‡ – еВМ‰ВОВВ‚‡ Б‡ФЛТ˚‚‡- ВЪТfl УНУМ˜‡ЪВО¸МУ ‚ ‚Л‰В

мМЛ‚В Т‡О¸М‡fl „‡БУ‚‡fl ФУТЪУflММ‡fl R – ˝ЪУ ‡·УЪ‡ ‡Т¯Л-ВМЛfl У‰МУ„У ПУОfl „‡Б‡ Ф Л М‡„ В‚‡МЛЛ М‡ У‰ЛМ „ ‡‰ЫТ Ф Л ФУТЪУflММУП ‰‡‚ОВМЛЛ.

з‡И‰ВП БМ‡˜ВМЛВ ЫМЛ‚В Т‡О¸МУИ „‡БУ‚УИ ФУТЪУflММУИ ‚ ТЛТЪВПВ ла

R = p0V0 = 101325 22, 4 /273 = 8314 ÑÊ/(ÍÏÓθ ä).

273

33

м ‡‚МВМЛВ дО‡ФВИ УМ‡ – еВМ‰ВОВВ‚‡ ¯Л УНУ ЛТФУО¸БЫВЪТfl ‰Оfl В¯ВМЛfl ПМУ„Лı Ф ‡НЪЛ˜ВТНЛı Б‡‰‡˜, МВТПУЪ fl М‡ ЪУ, ˜ЪУ УМУ ‚˚‚В‰ВМУ ‰Оfl Л‰В‡О¸М˚ı „‡БУ‚. СВОУ ‚ ЪУП, ˜ЪУ ФУ˜ЪЛ ‚ТВ „‡Б˚ Ф Л МВ У˜ВМ¸ МЛБНЛı ЪВПФВ ‡ЪЫ ‡ı, ‰‡ОВНЛı УЪ ЪУ˜НЛ НУМ‰ВМТ‡ˆЛЛ ‰‡ММУ„У „‡Б‡, Л Ф Л ‰‡‚ОВМЛflı, МВ У˜ВМ¸ ТЛО¸МУ Ф В‚˚¯‡˛˘Лı ‡ЪПУТЩВ МУВ, ФУ˜ЪЛ МВ УЪОЛ- ˜‡˛ЪТfl УЪ Л‰В‡О¸МУ„У „‡Б‡. нУО¸НУ Ф Л МЛБНЛı ЪВПФВ ‡ЪЫ ‡ı, Ф Л·ОЛК‡˛˘ЛıТfl Н ЪВПФВ ‡ЪЫ В НУМ‰ВМТ‡ˆЛЛ ‰‡ММУ„У „‡Б‡, ЛОЛ Ф Л ‰‡‚ОВМЛflı ‚ ТУЪМЛ Л Ъ˚Тfl˜Л ‡ЪПУТЩВ М‡·О˛‰‡˛ЪТfl Б‡ПВЪМ˚В УЪТЪЫФОВМЛfl УЪ Ы ‡‚МВМЛfl дО‡ФВИ УМ‡ – еВМ‰В- ОВВ‚‡, Л ЪУ„‰‡ М‡‰У ФУО¸БУ‚‡Ъ¸Тfl ‰ Ы„ЛП Ы ‡‚МВМЛВП ТУТЪУflМЛfl.

м ‡‚МВМЛВП дО‡ФВИ УМ‡ – еВМ‰ВОВВ‚‡ ‚ ‚Л‰В (1.19) ПУКМУ ФУО¸БУ‚‡Ъ¸Тfl ЪУ„‰‡, НУ„‰‡ ЛБ‚ВТЪМ‡ ПУОВНЫОfl М‡fl П‡ТТ‡ „‡- Б‡ ЛОЛ КВ НУ„‰‡ ВВ М‡‰У УФ В‰ВОЛЪ¸ ФУ ‰ Ы„ЛП ЛБ‚ВТЪМ˚П ‚В- ОЛ˜ЛМ‡П, ‚ıУ‰fl˘ЛП ‚ ЩУ ПЫОЫ (1.19).

у‡ТЪУ ‚ТЪ В˜‡˛ЪТfl Б‡‰‡˜Л, ‚ НУЪУ ˚ı ПУОВНЫОfl М‡fl П‡ТТ‡ „‡Б‡ МВЛБ‚ВТЪМ‡. щЪУ ПУКВЪ ·˚Ъ¸ ‚ „‡Б‡ı ТОУКМУ„У ТУТЪ‡‚‡. йФ В‰ВОЛЪ¸ ПУОВНЫОfl МЫ˛ П‡ТТЫ Ъ‡НУИ ТПВТЛ У·˚˜МУ Ъ Ы‰МУ, МУ Т ‡‚МЛЪВО¸МУ ОВ„НУ ПУКМУ УФ В‰ВОЛЪ¸ ВВ ФОУЪМУТЪ¸. нУ„‰‡ ПУКМУ ФУОЫ˜ЛЪ¸ В¯ВМЛВ Б‡‰‡˜Л, ФУО¸БЫflТ¸ Ы ‡‚МВМЛВП дО‡ФВИ УМ‡ – еВМ‰ВОВВ‚‡, ЪУО¸НУ ‡Т˜ВЪ „‡БУ‚УИ ФУТЪУflММУИ М‡‰У ‚ВТЪЛ МВ ФУ ПУОВНЫОfl МУИ П‡ТТВ µ, ‡ ФУ ФОУЪМУТЪЛ ρ „‡Б‡ Л УЪМУТЛЪ¸ ВВ МВ Н У‰МУПЫ ПУО˛, ‡ Н В‰ЛМЛˆВ П‡ТТ˚ „‡Б‡, М‡Ф ЛПВ , Н У‰МУПЫ НЛОУ„ ‡ППЫ. и Л Ъ‡НУП ‡Т˜ВЪВ МВО¸Бfl ФУОЫ˜ЛЪ¸ ЫМЛ‚В Т‡О¸МЫ˛ НУМТЪ‡МЪЫ, ‰Оfl Н‡К‰У„У „‡Б‡ ФУОЫ˜‡ВЪТfl Т‚УВ БМ‡˜ВМЛВ „‡БУ‚УИ ФУТЪУflММУИ B.

ÑÎfl Ó‰ÌÓ„Ó ÍËÎÓ„ ‡Ïχ ‚ÓÁ‰Ûı‡

B = p0 1 , 273 ρ‚

Á‰ÂÒ¸ p0 – ‡ЪПУТЩВ МУВ ‰‡‚ОВМЛВ, и‡; p0 = 1,293 Í„/Ï3 – ФОУЪМУТЪ¸ ‚УБ‰Ыı‡ Ф Л МУ П‡О¸М˚ı ЫТОУ‚Лflı.

ЗПВТЪУ V0 ‚‚В‰ВП Ы‰ВО¸М˚И У·˙ВП 1/ρ – У·˙ВП, Б‡МflЪ˚И У‰МЛП НЛОУ„ ‡ППУП ‚УБ‰Ыı‡. иУ‰ТЪ‡‚Л‚ БМ‡˜ВМЛfl, ‚ ТЛТЪВПВ

МЛВ „‡БУ‚УИ ФУТЪУflММУИ ‰Оfl У‰МУ„У НЛОУ„ ‡ПП‡ ‚УБ‰Ыı‡.

СОfl ‰ Ы„У„У „‡Б‡ БМ‡˜ВМЛВ ФУТЪУflММУИ B ‚ ТЛТЪВПВ ла ФУОЫ˜ЛП, ‡Б‰ВОЛ‚ ˜ЛТОУ 287,05 М‡ УЪМУТЛЪВО¸МЫ˛ ФОУЪМУТЪ¸ „‡- Б‡ ФУ ‚УБ‰ЫıЫ ρ :

B = 287,05/ ρ .

34

1.2.4. мкДЗзЦзаЦ лйлнйьзаь кЦДгъзхп ЙДбйЗ

щНТФВ ЛПВМЪ‡О¸М‡fl Ф У‚В Н‡ Ы ‡‚МВМЛfl (1.19), Ф У‚В‰ВММ‡fl ПМУ„ЛПЛ ЛТТОВ‰У‚‡ЪВОflПЛ, ФУН‡Б‡О‡, ˜ЪУ ЛБПВМВМЛВ Т‚УИТЪ‚В‡О¸М˚ı „‡БУ‚ Ф Л ‚˚ТУНЛı ‰‡‚ОВМЛflı МВО¸Бfl УФЛТ‡Ъ¸ ˝ЪУИ Б‡‚ЛТЛПУТЪ¸˛.

ЙУОО‡М‰ТНЛИ ЩЛБЛН З‡М-‰В -З‡‡О¸Т ‚ 1879 „. Ф В‰ОУКЛО Ы˜ВТЪ¸ ТУ·ТЪ‚ВММ˚И У·˙ВП ПУОВНЫО „‡Б‡ Л ТЛО˚ Лı ‚Б‡ЛПМУ„У Ф ЛЪflКВМЛfl ФУТ В‰ТЪ‚УП ‚‚В‰ВМЛfl ‰УФУОМЛЪВО¸М˚ı ˜ОВМУ‚ ‚ Ы ‡‚МВМЛВ дО‡ФВИ УМ‡ – еВМ‰ВОВВ‚‡:

= V/G – Û‰ÂθÌ˚È Ó·˙ÂÏ „‡Á‡, Ï3/Í„; b – ФУФ ‡‚Н‡ М‡ ТУ·- ТЪ‚ВММ˚И У·˙ВП ПУОВНЫО, П3/Í„.

З Ы ‡‚МВМЛЛ (1.20) ТО‡„‡ВПУВ a/v2 ‚˚ ‡К‡ВЪ ‚МЫЪ ВММВВ ‰‡‚ОВМЛВ, НУЪУ УВ fl‚ОflВЪТfl Н‡Н ·˚ ‡‚МУ‰ВИТЪ‚Ы˛˘ВИ ТЛО Ф ЛЪflКВМЛfl ‚ТВı ПУОВНЫО ‚ У·˙ВПВ V. éÌÓ Ô Ë·‡‚ÎflÂÚÒfl Í ‚̯ÌÂÏÛ ‰‡‚ÎÂÌ˲.

LJÌ-‰Â -LJ‡Î¸Ò ̇¯ÂÎ, ˜ÚÓ ÔÓÔ ‡‚͇ b М‡ ТУ·ТЪ‚ВММ˚И У·˙ВП ПУОВНЫО, ЛПВ˛˘Лı ¯‡ УУ· ‡БМЫ˛ ЩУ ПЫ, ‡‚М‡ Ы˜ВЪ- ‚В ВММУПЫ У·˙ВПЫ ПУОВНЫО.

м ‡‚МВМЛВ (1.20) Ф Л·ОЛКВММУВ. дУ˝ЩЩЛˆЛВМЪ˚ a Ë b ‚ ‰ВИТЪ‚ЛЪВО¸МУТЪЛ fl‚Оfl˛ЪТfl ТОУКМ˚ПЛ ЩЫМНˆЛflПЛ У·˙ВП‡, ЪВПФВ ‡ЪЫ ˚, ЩУ П˚ ПУОВНЫО „‡Б‡.

„‰Â R = 8314,3 ÑÊ/(ÍÏÓθ ä).

д Л Ъ Л˜ ВТ Н ‡fl Ъ ВП Ф В ‡Ъ Ы ‡ ˜ЛТЪУ„У ‚В˘ВТЪ‚‡ – ˝ЪУ П‡НТЛП‡О¸М‡fl ЪВПФВ ‡ЪЫ ‡, Ф Л НУЪУ УИ КЛ‰Н‡fl Л Ф‡ У‚‡fl Щ‡Б˚ ПУ„ЫЪ ТУТЫ˘ВТЪ‚У‚‡Ъ¸ ‚ ‡‚МУ‚ВТЛЛ, ЛОЛ Ъ‡ ЪВПФВ ‡ЪЫ-‡, Ф Л НУЪУ УИ Т В‰Мflfl ПУОВНЫОfl М‡fl НЛМВЪЛ˜ВТН‡fl ˝МВ „Лfl

ТЪ‡МУ‚ЛЪТfl ‡‚МУИ ФУЪВМˆЛ‡О¸МУИ ˝МВ „ЛЛ Ф ЛЪflКВМЛfl ПУОВНЫО. и Л ·УОВВ ‚˚ТУНУИ ЪВПФВ ‡ЪЫ В ТЫ˘ВТЪ‚У‚‡МЛВ КЛ‰НУИ Щ‡Б˚ МВ‚УБПУКМУ.

С‡‚ОВМЛВ Ф‡ У‚ ‚В˘ВТЪ‚‡ Ф Л Н ЛЪЛ˜ВТНУИ ЪВПФВ ‡ЪЫ В М‡Б˚‚‡ВЪТfl Н Л Ъ Л˜ ВТ Н ЛП ‰ ‡‚ О ВМ ЛВ П, ‡ У·˙ВП ‚В˘ВТЪ‚‡, УЪМВТВММ˚И Н У‰МУПЫ ПУО˛ ЛОЛ ‰ Ы„УИ В‰ЛМЛˆВ П‡ТТ˚ ‚В˘В- ТЪ‚‡, М‡Б˚‚‡ВЪТfl Н Л Ъ Л˜ ВТ Н ЛП Ы ‰В О¸ М ˚П У ·˙ В П УП .

35

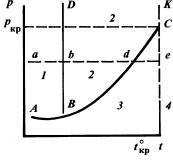
кЛТ. 1.3. СЛ‡„ ‡ПП‡ Б‡‚ЛТЛПУТЪЛ ‰‡‚ОВМЛfl УЪ ЪВПФВ ‡ЪЫ ˚ ‰Оfl ЛМ‰Л‚Л‰Ы‡О¸- МУ„У НУПФУМВМЪ‡. лУТЪУflМЛfl:

1 – Ú‚Â ‰ÓÂ; 2 – ÊˉÍÓÂ; 3 – Ô‡ ÓÓ·-‡ÁÌÓÂ; 4 – „‡ÁÓÓ· ‡ÁÌÓÂ

з‡ ЛТ. 1.3. Ф Л‚В‰ВМ‡ Б‡‚ЛТЛПУТЪ¸ ‰‡‚ОВМЛfl (ЫФ Ы„УТЪЛ М‡Т˚˘ВММ˚ı Ф‡ У‚) ˜ЛТЪ˚ı ‚В˘ВТЪ‚ УЪ ЪВПФВ ‡ЪЫ ˚.

лУБ‰‡МЛВ ·УОВВ ЪУ˜МУ„У Ы ‡‚МВМЛfl ТУТЪУflМЛfl Ф Л У‰М˚ı „‡БУ‚, ТФУТУ·МУ„У Ф ‡‚ЛО¸МУ УФЛТ˚‚‡Ъ¸ ЛБПВМВМЛВ Лı Т‚УИТЪ‚ ‚ Ф УˆВТТ‡ı ‰У·˚˜Л Л ФВ В ‡·УЪНЛ Ф Л У‰М˚ı „‡БУ‚, ¯ОУ ‚ ‰‚Ыı М‡Ф ‡‚ОВМЛflı:

‰УФУОМВМЛВ Ы ‡‚МВМЛfl ТУТЪУflМЛfl Л‰В‡О¸МУ„У „‡Б‡ ·УО¸¯ЛП ˜ЛТОУП НУМТЪ‡МЪ;

‚‚‰ÂÌË ÔÓÔ ‡‚Ó˜ÌÓ„Ó ÍÓ˝ÙÙˈËÂÌÚ‡ z ‚ Ы ‡‚МВМЛВ ТУТЪУflМЛfl Л‰В‡О¸МУ„У „‡Б‡ (1.18), Ы˜ЛЪ˚‚‡˛˘В„У УЪНОУМВМЛВ В- ‡О¸МУ„У „‡Б‡ УЪ Л‰В‡О¸МУ„У,

С. Е ‡ЫМ Л С. д‡Ъˆ М‡ УТМУ‚‡МЛЛ ЛБЫ˜ВМЛfl ВБЫО¸Ъ‡ЪУ‚ ˝НТФВ ЛПВМЪ‡О¸М˚ı ЛБПВ ВМЛИ НУ˝ЩЩЛˆЛВМЪ‡ Т‚В ıТКЛП‡В- ПУТЪЛ ЫТЪ‡МУ‚ЛОЛ, ˜ЪУ ВТОЛ Ф Л‚В‰ВММ˚В Ф‡ ‡ПВЪ ˚ ‡БОЛ˜- М˚ı Ф Л У‰М˚ı „‡БУ‚ У‰ЛМ‡НУ‚˚ (pÔ , TÔ ), ЪУ УМЛ М‡ıУ‰flЪТfl ‚ ТУУЪ‚ВЪТЪ‚ВММ˚ı ТУТЪУflМЛflı, Ф Л НУЪУ ˚ı Лı ЩЛБЛ˜ВТНЛВ Т‚УИТЪ‚‡ (z, ФОУЪМУТЪ¸ Л ‰ .) У‰ЛМ‡НУ‚˚, Ъ.В. z = z(pÔ , TÔ ).

и Л ‚ В‰ ВМ М ˚П Л Ф ‡ ‡П ВЪ ‡П Л М‡Б˚‚‡˛Ъ ·ВБ ‡БПВ - М˚В ‚ВОЛ˜ЛМ˚, ФУН‡Б˚‚‡˛˘ЛВ, ‚У ТНУО¸НУ ‡Б ‰ВИТЪ‚ЛЪВО¸- М˚В Ф‡ ‡ПВЪ ˚ ТУТЪУflМЛfl „‡Б‡ (‰‡‚ОВМЛВ, ЪВПФВ ‡ЪЫ ‡, У·˙- ВП, ФОУЪМУТЪ¸, НУ˝ЩЩЛˆЛВМЪ Т‚В ıТКЛП‡ВПУТЪЛ) ·УО¸¯В ЛОЛ ПВМ¸¯В Н ЛЪЛ˜ВТНЛı:

pÔ =p/pÍ ; TÔ =T/TÍ ; vÔ =v/vÍ ; ρÔ =ρ/ρÍ ; zÔ =z/zÍ .

з‡ ЛТ. 1.4 Ф Л‚В‰ВМ‡ Б‡‚ЛТЛПУТЪ¸ НУ˝ЩЩЛˆЛВМЪ‡ Т‚В ı- ТКЛП‡ВПУТЪЛ Ф Л У‰МУ„У „‡Б‡ z ÓÚ pÔ Ë TÔ . еУОВНЫО˚ Ф У- ТЪ˚ı „‡БУ‚ (ПВЪ‡М, „ВОЛИ, ‡ „УМ, Н ЛФЪУМ, НТВМУМ Л ‰ .) ЛПВ- ˛Ъ ТЩВ Л˜ВТНЫ˛ ЩУ ПЫ, ПУОВНЫО˚ ТОУКМ˚ı „‡БУ‚ Л КЛ‰НУТЪВИ – МВТЩВ Л˜ВТНЫ˛.

СОfl ТОУКМ˚ı „‡БУ‚ Л КЛ‰НУТЪВИ ТЛО˚ Ф ЛЪflКВМЛfl (ЛОЛ УЪ-

36

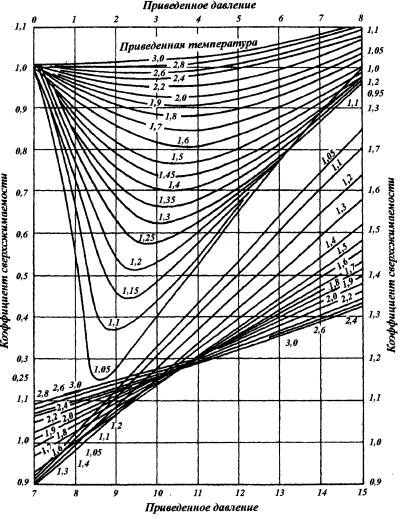
кЛТ. 1.4. ᇂЛТЛПУТЪ¸ НУ˝ЩЩЛˆЛВМЪ‡ Т‚В ıТКЛП‡ВПУТЪЛ Ф Л У‰МУ„У „‡Б‡ УЪ Ф Л‚В‰ВММ˚ı ‡·ТУО˛ЪМ˚ı ‰‡‚ОВМЛfl Л ЪВПФВ ‡ЪЫ ˚

Ъ‡ОНЛ‚‡МЛfl) ПВК‰Ы ‡БОЛ˜М˚ПЛ „ ЫФФ‡ПЛ ПУОВНЫОfl М˚ı Ф‡ ЪУ˜МУ МВ ПУ„ЫЪ ·˚Ъ¸ Ф В‰ТЪ‡‚ОВМ˚ ОЛ¯¸ У‰МУИ ТЛОУИ Ф ЛЪflКВМЛfl ПВК‰Ы ˆВМЪ ‡ПЛ ПУОВНЫО. СОfl Ы˜ВЪ‡ ‰ Ы„Лı, МВˆВМЪ Л˜- М˚ı ТЛО ‚‚У‰ЛЪТfl ‡ˆВМЪ Л˜ВТНЛИ Щ‡НЪУ ω, УˆВМЛ‚‡˛˘ЛИ ПВ Ы УЪНОУМВМЛfl НУ˝ЩЩЛˆЛВМЪ‡ Т‚В ıТКЛП‡ВПУТЪЛ Ф Л У‰- М˚ı „‡БУ‚ УЪ В„У БМ‡˜ВМЛfl, УФ В‰ВОflВПУ„У ФУ pÔ Ë TÔ :

37

z = z(pÔ , TÔ , ω)

ËÎË zÒÏ = z0(pÔ , TÔ ) + z1(pÔ , TÔ )ωÒÏ,

„‰Â z0(pÔ , TÔ ) – НУ˝ЩЩЛˆЛВМЪ Т‚В ıТКЛП‡ВПУТЪЛ Ф УТЪУ„У

„‡Á‡, ÓÔ Â‰ÂÎflÂÏ˚È ÔÓ ‰‡ÌÌ˚Ï pÔ Ë TÔ ; z1(pÔ , TÔ ) – ФУ- Ф ‡‚Н‡ Н У·У·˘ВММУПЫ НУ˝ЩЩЛˆЛВМЪЫ Т‚В ıТКЛП‡ВПУТЪЛ

ТОУКМ˚ı „‡БУ‚ Л КЛ‰НУТЪВИ, fl‚Оfl˛˘‡flТfl ЩЫМНˆЛВИ Ф Л‚В‰ВММУ„У ‰‡‚ОВМЛfl Л ЪВПФВ ‡ЪЫ ˚; ωÒÏ – ‡ˆВМЪ Л˜ВТНЛИ Щ‡НЪУ ТПВТЛ „‡БУ‚ (‰Оfl Ф УТЪ˚ı „‡БУ‚ ωÒÏ = 0),

„‰Â yi – ÏÓÎfl ̇fl ‰ÓÎfl i-„У НУПФУМВМЪ‡ ‚ ТПВТЛ; ωi – ‡ˆВМ- Ъ Л˜ВТНЛИ Щ‡НЪУ i-„У НУПФУМВМЪ‡ ‚ ТПВТЛ, НУЪУ ˚И ПУКМУ УФ В‰ВОЛЪ¸ ФУ ЩУ ПЫОВ щ‰ПЛТЪВ ‡:

„‰Â p‡Ú – ‡ЪПУТЩВ МУВ ‰‡‚ОВМЛВ; TÍËÔ – ЪВПФВ ‡ЪЫ ‡ НЛФВМЛfl НУПФУМВМЪ‡ Ф Л ‡ЪПУТЩВ МУП ‰‡‚ОВМЛЛ.

ДˆВМЪ Л˜ВТНЛИ Щ‡НЪУ ‰Оfl ПМУ„Лı ‚В˘ВТЪ‚ ЛБПВМflВЪТfl УЪ 0 ‰У 0,4 (ТП. Ъ‡·О. 1.5, 1.7).

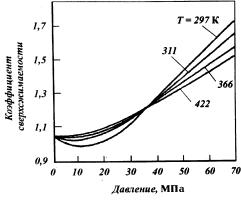
з‡ ЛТ. 1.5. ФУН‡Б‡М˚ Б‡‚ЛТЛПУТЪЛ НУ˝ЩЩЛˆЛВМЪ‡ Т‚В ıТКЛП‡ВПУТЪЛ ‡БУЪ‡ УЪ ‰‡‚ОВМЛfl Л ЪВПФВ ‡ЪЫ ˚.

кЛТ. 1.5. ᇂЛТЛПУТЪ¸ НУ˝Щ- ЩЛˆЛВМЪ‡ Т‚В ıТКЛП‡ВПУТЪЛ ‡БУЪ‡ УЪ ‰‡‚ОВМЛfl Л ЪВПФВ ‡ЪЫ ˚

38

н‡НКВ Ф ЛПВМfl˛ЪТfl Ы ‡‚МВМЛfl ТУТЪУflМЛfl кВ‰ОЛı‡ – д‚УМ- „‡, ЕВМВ‰ЛНЪ‡ – ЗВ··‡ – кЫ·ЛМ‡, иВМ„‡ – кУ·ЛМТУМ‡ Л ‰ .

З ‡Т˜ВЪ‡ı Ф УˆВТТУ‚ ‰У·˚˜Л, Ъ ‡МТФУ Ъ‡ Л ФВ В ‡·УЪНЛ Ф Л У‰МУ„У „‡Б‡ ¯Л УНУВ Ф ЛПВМВМЛВ М‡ıУ‰ЛЪ ‰‚ЫıНУМТЪ‡МЪМУВ Ы ‡‚МВМЛВ ТУТЪУflМЛfl кВ‰ОЛı‡ – д‚УМ„‡, fl‚Оfl˛˘ВВТfl У‰- МУИ ЛБ ПУ‰ЛЩЛН‡ˆЛИ Ы ‡‚МВМЛfl ТУТЪУflМЛfl З‡М-‰В -З‡‡О¸Т‡:

„‰Â a = 0,4275 R2T2,5Í /pÍ ; b – 0,08664 RTÍ /pÍ ; TÍ – Н ЛЪЛ- ˜ВТН‡fl ЪВПФВ ‡ЪЫ ‡ (ЪВПФВ ‡ЪЫ ‡, ‚˚¯В НУЪУ УИ „‡Б МВ ФВ В-

ıУ‰ЛЪ ‚ КЛ‰НУВ ТУТЪУflМЛВ); pÍ – Н ЛЪЛ˜ВТНУВ ‰‡‚ОВМЛВ.

СОfl УФ В‰ВОВМЛfl НУ˝ЩЩЛˆЛВМЪ‡ z Ы ‡‚МВМЛВ кВ‰ОЛı‡ – д‚УМ„‡ (кд) ЛПВВЪ ‚Л‰

ÌÓ ÍÓ˝ÙÙˈËÂÌÚ˚ Â„Ó ‚˚˜ËÒÎfl˛Ú ÔÓ ÒÎÂ‰Û˛˘ËÏ Ô ‡‚Ë·Ï:

З Н ЛЪЛ˜ВТНУИ У·О‡ТЪЛ, ‡ Ъ‡НКВ Ф Л УФ В‰ВОВМЛЛ Ф‡ ‡ПВЪ-У‚ ТПВТВИ, ТУТЪУfl˘Лı ЛБ ПУОВНЫО ‡БОЛ˜МУ„У ТЪ УВМЛfl, ФУ- „ В¯МУТЪ¸ ‡Т˜ВЪУ‚ ВБНУ ‚УБ ‡ТЪ‡ВЪ. д УПВ ЪУ„У, Ф‡ ‡ПВЪ-˚ ‚В˘ВТЪ‚ Л ТПВТВИ ‚ КЛ‰НУП ТУТЪУflМЛЛ Ъ‡НКВ ‚˚˜ЛТОfl˛Ъ- Тfl Т ·УО¸¯УИ ФУ„ В¯МУТЪ¸˛.

иУ˝ЪУПЫ иВМ„ Л кУ·ЛМТУМ Ф В‰Ф ЛМflОЛ ФУФ˚ЪНЫ ‚МВТЪЛ Ъ‡НЛВ ЛБПВМВМЛfl ‚ ‚Л‰ Ы ‡‚МВМЛfl кд, НУЪУ ˚В ·˚ ФУ‚˚ТЛОЛ ЪУ˜МУТЪ¸ ‚˚˜ЛТОВМЛfl ФОУЪМУТЪЛ ‡‚МУ‚ВТМУИ КЛ‰НУТЪЛ Щ‡Б˚.

м ‡‚МВМЛВ ТУТЪУflМЛfl иВМ„‡ – кУ·ЛМТУМ‡ ЛПВВЪ ‚Л‰

V − b V(V + b) + b(V − b)

„‰Â V – ÏÓÎfl Ì˚È Ó·˙ÂÏ, a Ë b – НУ˝ЩЩЛˆЛВМЪ˚ Ы ‡‚МВМЛfl, УФ В‰ВОflВП˚В Н ЛЪЛ˜ВТНЛПЛ Ф‡ ‡ПВЪ ‡ПЛ ‚В˘ВТЪ‚‡.

äÓ˝ÙÙˈËÂÌÚ a – ЩЫМНˆЛfl ЪВПФВ ‡ЪЫ ˚ a(T) = apRα(T),

„‰Â apR, α(T) – ÍÓ˝ÙÙˈËÂÌÚ˚, ÓÔ Â‰ÂÎflÂÏ˚ ÔÓ ÙÓ ÏÛ·Ï

α = [1 + m(1 − T 0,5Ô )]2;

apR = 0, 45724R2TÍ2 / pÍ .

39

äÓ˝ÙÙˈËÂÌÚ b ЛПВВЪ ‚Л‰

b = 0, 0778RTÍ / pÍ .

СОfl ‚˚˜ЛТОВМЛfl НУ˝ЩЩЛˆЛВМЪ‡ m ЛТФУО¸БЫ˛Ъ ЩУ ПЫОЫ m = 0,37464 + 1, 54226ω − 0,26992ω2.

м ‡‚МВМЛВ (1.27), Б‡ФЛТ‡ММУВ УЪМУТЛЪВО¸МУ НУ˝ЩЩЛˆЛВМЪ‡ Т‚В ıТКЛП‡ВПУТЪЛ z, ЛПВВЪ ‚Л‰

z 3 − (1 − B)z 2 + (A − 3B2 − 2B)z − (AB − B2 − B3) = 0. (1.28)

дУ˝ЩЩЛˆЛВМЪЫ Т‚В ıТКЛП‡ВПУТЪЛ Ф‡ У‚УИ („‡БУ‚УИ) Щ‡Б˚ ТУУЪ‚ВЪТЪ‚ЫВЪ М‡Л·УО¸¯ЛИ ФУОУКЛЪВО¸М˚И ‰ВИТЪ‚ЛЪВО¸М˚И НУ ВМ¸ (1.19), ‡ НУ˝ЩЩЛˆЛВМЪЫ Т‚В ıТКЛП‡ВПУТЪЛ КЛ‰НУИ Щ‡Б˚ – М‡ЛПВМ¸¯ЛИ ФУОУКЛЪВО¸М˚И ‰ВИТЪ‚ЛЪВО¸М˚И НУ ВМ¸ (1.19).

СОfl ‰‚ЫıНУМТЪ‡МЪМ˚ı НЫ·Л˜ВТНЛı Ы ‡‚МВМЛИ ТУТЪУflМЛfl БМ‡˜ВМЛВ НУ˝ЩЩЛˆЛВМЪ‡ Т‚В ıТКЛП‡ВПУТЪЛ О˛·У„У ‚В˘ВТЪ‚‡ ‚ Н ЛЪЛ˜ВТНУИ ЪУ˜НВ ФУОЫ˜‡ВЪТfl У‰ЛМ‡НУ‚˚П. н‡Н, ‰Оfl ПУ‰Л- ЩЛН‡ˆЛЛ лУ‡‚В zÍ = 0,333, ‡ ‰Оfl ПУ‰ЛЩЛН‡ˆЛЛ иВМ„‡ – кУ- ·ЛМТУМ‡ – 0,307. З ‰ВИТЪ‚ЛЪВО¸МУТЪЛ БМ‡˜ВМЛВ ˝ЪУ„У НУ˝Щ- ЩЛˆЛВМЪ‡ ‚ Н ЛЪЛ˜ВТНУИ ЪУ˜НВ ПВМflВЪТfl УЪ 0,288 ‰Оfl ПВЪ‡М‡ ‰У 0,212 ‰Оfl М-МУМ‡‰ВН‡М‡. н‡НЛП У· ‡БУП, zÍ Ы ‡‚МВМЛfl иВМ- „‡ – кУ·ЛМТУМ‡ ‚ ·УО¸¯ВИ ТЪВФВМЛ ТУУЪ‚ВЪТЪ‚ЫВЪ ˜ЛТЪ˚П Ы„- ОВ‚У‰У У‰‡П, ˜ВП БМ‡˜ВМЛВ zÍ Û ‡‚ÌÂÌËfl ëÓ‡‚Â.

дУ˝ЩЩЛˆЛВМЪ˚ Ы ‡‚МВМЛfl (1.27) ‰Оfl ТПВТЛ ‚˚˜ЛТОfl˛Ъ ФУ Ф ‡‚ЛОЫ ТПВ¯Л‚‡МЛfl

„‰Â cij – ÍÓ˝ÙÙˈËÂÌÚ˚ Ô‡ ÌÓ„Ó ‚Á‡ËÏÓ‰ÂÈÒÚ‚Ëfl; ηi, ηj – ÒÓÓÚ‚ÂÚÒÚ‚ÂÌÌÓ ÏÓÎfl Ì˚ ‰ÓÎË i-„Ó Ë j-„У НУПФУМВМЪУ‚ ‚ ТПВТЛ;

a= apRαi (T).

1.3.йлзйЗзхЦ иДкДеЦнкх икакйСзйЙй ЙДбД

1.3.1.игйнзйлнъ ЙДбйЗ

иУ‰ ФОУЪМУТЪ¸˛ „‡Б‡ ФУМЛП‡˛Ъ УЪМУ¯ВМЛВ П‡ТТ˚ „‡Б‡ Н В„У У·˙ВПЫ. Ц‰ЛМЛˆ‡ ЛБПВ ВМЛfl ФОУЪМУТЪЛ ‚ ла – НЛОУ- „ ‡ПП М‡ НЫ·Л˜ВТНЛИ ПВЪ (Н„/П3).

иОУЪМУТЪ¸ „‡Б‡ ρ0 (‚ Í„/Ï3) ‚ МУ П‡О¸М˚ı ЩЛБЛ˜ВТНЛı ЫТОУ‚Лflı (Ф Л 0,1013 еи‡ Л 273 д) ПУКМУ УФ В‰ВОЛЪ¸ ФУ В„У ПУОВНЫОfl МУИ П‡ТТВ M:

40