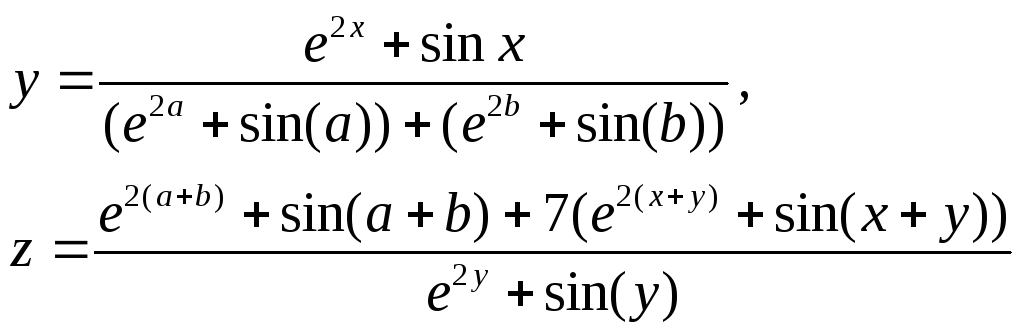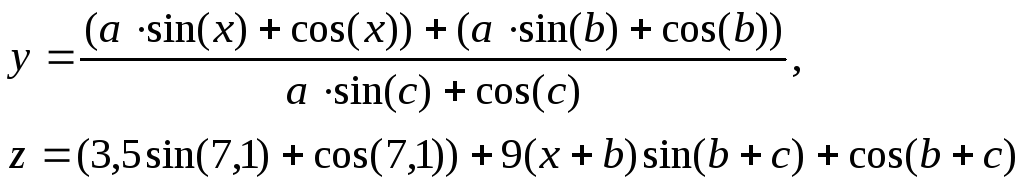131

5.2 Контрольная работа № 2

Задание 1.

Составить программу вычисления значений переменных, используя функции пользователя. Варианты заданий представлены в таблице 5.4.

Задание 2.

Приближенное решение нелинейных уравнений. Варианты заданий представлены в таблице 5.5.

1. Отделить вещественные корни алгебраического уравнения аналитическим способом, используя понятие критических точек и формулу определения промежутка существования вещественных корней.

2. Уточнить вручную один из корней указанным методом, осуществив четыре итерации (4 шага вычисления).

3. Составить программу реализации на ЭВМ указанного в варианте метода, пользуясь блок-схемами алгоритмов численных методов, представленными в Приложении 6.

4. Вычислить все корни уравнения с точностью =10^-4, используя программу.

Задание 3.

Приближенное вычисление определенных интегралов. Варианты заданий представлены в таблице 5.6.

1. Вычислить вручную определенный интеграл указанным в варианте методом, приняв число интервалов разбиения отрезка интегрирования n=6.

2. Составить программу реализации на ЭВМ указанного в варианте метода, пользуясь блок-схемами алгоритмов численных методов, представленными в Приложении 6.

3. Вычислить определенный интеграл с заданной точностью =10^-4, используя программу.

Задание 4.

Приближенное интегрирование дифференциальных уравнений. Варианты заданий представлены в таблице 5.7.

1. Составить программу интегрирования дифференциального уравнения методом Эйлера на участке [0; 1] с шагом h=0.1, пользуясь блок-схемой алгоритма метода, представленной в Приложении 6 и получить результаты на ЭВМ.

2. Составить программу интегрирования дифференциального уравнения методом Рунге-Кутта четвертого порядка на отрезке [0; 1] с шагом h=0.1, пользуясь блок-схемой алгоритма метода, представленной в Приложении 6 и получить результаты на ЭВМ.

Задание 5.

Приближенное решение систем линейных уравнений. Варианты заданий представлены в таблице 5.8.

1. Найти вручную значения неизвестных системы, выполнив три итерации (три шага вычислений) указанным методом.

2. Составить программу реализации на ЭВМ указанного метода, пользуясь блок-схемами алгоритмов численных методов, представленными в Приложении 6.

3. Решить систему с точностью =10^-5, используя программу.

Примечание: для четных вариантов использовать метод простых итераций, для нечетных – метод итераций Зейделя.

Задание 6.

Аппроксимация и интерполяция функций. Варианты заданий представлены в таблице 5.9.

1. Составить программу нахождения коэффициентов a, b, c методом наименьших квадратов для параболической зависимости вида y=ax²+bx+c. При решении системы линейных уравнений использовать расчетные формулы пункта 4.5.2 Главы 4.

2. Вычислить коэффициенты a, b, c с использованием данных, указанных в варианте, и найти значения функции y для заданных аргументов x1 и x2.

3. Составить программу нахождения значений функции y для заданных аргументов x1 и x2, используя квадратичную интерполяцию.

4. Сравнить значения функции y для заданных аргументов x1 и x2, полученные по методу наименьших квадратов и методу квадратичной интерполяции.

5. При составлении программ можно воспользоваться блок-схемами алгоритмов численных методов, представленными в Приложении 6.

Задание 1.

Таблица 5.4 – Варианты заданий

Номер варианта		Расчетные формулы		Исходные данные
1		2		3
1				а=1,7; в=4; х=1,2
2				x=; a=7,2; c=/3; b=/6
3				a=2,3; b=7,4; c=12,9
4				a=9,4; b=11,5; c=12,7
5		,		a=4,3; b=7,9; c=11,3 d=12,7
6			b=11,5; a=9,4; c=12,7
7			c=1,5; a=2,3; b=2,4
8	,		a=7,3; b=12,1; c=3,4