
Контрольная работа № 2 надежность
.docxМИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
Ухтинский государственный технический университет
Факультет информационных технологий
Кафедра автоматизированных информационных систем
КОНТРОЛЬНАЯ РАБОТА 2
по дисциплине «Надежность, эргономичность качество АСОИУ»
Шифр: 081754
Вариант: 7
Домашний адрес:
г. Вуктыл
ул. Газовиков
д. 4, кв. 37
Выполнил:
студент группы АИС-08(к) Шамсутдинова Г.А.
Проверил:
Заведующий кафедрой АИС Куделин А.Г.
Ухта 2013
СОДЕРЖАНИЕ
1 ПОСТАНОВКА ЗАДАЧИ
Рассчитать вероятность безотказной работы и вероятность отказа системы по заданной структурной схеме надежности к моменту времени t=5000 ч. Расчет произвести следующими методами:
1) методом минимальных путей и сечений;
2) методом разложения относительно особого элемента;
3) методом преобразования «треугольник – звезда».

Рисунок 1 – Мостиковая схема
Время наработки до отказа у элементов имеет следующие законы распределения:
-
экспоненциальный λ=1,3x10-4 (1/ч);
-
экспоненциальный λ=2,4x10-4;
-
нормальный m=6000, σ =1300;
-
нормальный m=7500 ч, σ =1500 ч;
-
экспоненциальный λ=4,7х10-4;
-
экспоненциальный λ=4,25x10-4;
-
экспоненциальный λ=3,42x10-4.
-
ПРАКТИЧЕСКАЯ ЧАСТЬ
-
Метод минимальных путей и сечений
Данный метод дает более точные оценки интервалов надежности.
Минимальным путем (или мини – путем) называется множество элементов системы, для которого выполняются два свойства:
1) если все элементы, принадлежащие мини-путям, работают, то система работает;
2) если отказали все элементы, не принадлежащие мини-путям и хоть один из элементов мини-путей, то система откажет.
A. Для последовательного соединения единственным мини-путем является все множество элементов системы.
B. Для параллельного соединения каждый элемент системы является отдельным мини-путем. Других мини-путей нет.
C. Для мостиковой схемы определим все мини-пути:
{1,2}, {1,6,4}, {3,6,2}, {3,4}, {5,7}.
Пусть для имеющейся системы найдены все мини-пути. При этом некоторые элементы системы могут принадлежать и нескольким мини-путям.
Мини-путь назовем работающим, если работают все входящие в него элементы.
Вероятность работы мини-пути равна произведению вероятностей работы всех входящих в этот мини-путь элементов. Поэтому каждому мини-пути сопоставим систему из последовательно соединенных элементов этого мини-пути.
Если хоть один из мини-путей системы работает, то работает вся система. И наоборот, если все мини – пути не работают, то и система откажет. Таким образом, отказ системы заключается в отказе всех мини-путей.
Итак, методика получения оценки надежности:
-
находим все мини – пути системы;
-
элементы каждого мини-пути соединяем последовательно;
-
все полученные на предыдущем шаге системы с последовательным соединением соединяем параллельно.
Полученная система с последовательно – параллельным соединением имеет не меньшую надежность, чем исходная система.
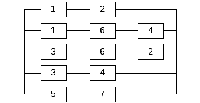
Рисунок 2 – Параллельное соединение мини – путей мостиковой схемы
Рассчитаем вероятности для каждого элемента системы. Для экспоненциального закона надежности вероятность рассчитывается по формуле 1:
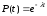 (1)
(1)

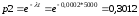
Для нормального закона распределения вероятность рассчитывается по следующим формулам 2, 3, 4:
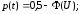 (2)
(2)
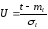 ; (3)
; (3)
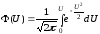 (4);
(4);
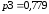
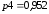


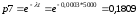
Надежность этой системы будет рассчитываться по формуле 5:
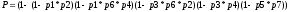 (5)
(5)
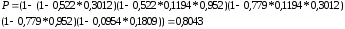
Вероятность отказа будет равна:
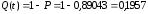
-
Метод разложения относительно особого элемента
В системе выбирается
элемент с наибольшим числом связей с
другими элементами. Этот элемент
называется особым. Обозначим надежность
этого элемента
 ,
вероятность отказа через
,
вероятность отказа через
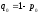 .
.
Предположим, что
особый элемент работоспособен. Тогда
получим новую структурную схему
надежности. Допустим, что новая схема
является последовательно-параллельным
соединением и мы можем рассчитать ее
надежность
 .
В данном случае говорят, что новая схема
получена из исходной "замыканием"
особого элемента.
.
В данном случае говорят, что новая схема
получена из исходной "замыканием"
особого элемента.
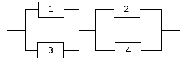
Рисунок 3 – Мостиковая схема после замыкания
Для мостиковой схемы на рисунке 1 особым элементом, имеющим наибольшее число связей, является элемент 6. При замыкании получаем структурную схему на рисунке 3.
Надежность новой схемы будет рассчитываться по формуле (6):
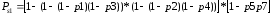 (6)
(6)

Предположим, что
особый элемент отказал. Тогда получим
еще одну структурную схему. Если она
будет последовательно-параллельным
соединением, то опять мы можем рассчитать
ее надежность
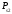 .В
последнем случае говорят, что схема
получена из исходной "обрывом"
особого элемента.
.В
последнем случае говорят, что схема
получена из исходной "обрывом"
особого элемента.
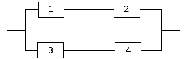
Рисунок 4 – Мостиковая схема после обрыва
Надежность этой схемы будет рассчитываться по формуле 7:
 (7)
(7)
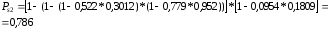
Следовательно, для всей системы вероятность безотказной работы будет вычисляться по формуле 8:
 (8)
(8)
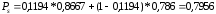
Вероятность отказа равна:

-
Метод преобразования «треугольник – звезда»
Допустим, что в
структурной схеме можно выделить
следующий участок (соединение
"треугольником"), состоящий из трех
элементов с надежностью
 (рисунок 5).
(рисунок 5).

Рисунок 5 – Соединение «треугольником»
Идея метода в том,
что мы заменяем этот участок в схеме
другим соединением, называемым "звездой",
состоящим из трех других элементов,
имеющих некоторые надежности
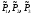 (рисунок 6).
(рисунок 6).

Рисунок 6 – Соединение «звездой»
Надежность системы при такой замене не должна измениться. Это означает, что вероятность работоспособности связки элементов А и В должна быть одинаковой как для «треугольника», так и для «звезды». То же самое должно выполняться для вероятностей работоспособности связок А и С, В и С.
Для соединения «треугольником» вероятность работоспособности связок А и В, А и С, В и С можно рассчитать по формулам 9, 10, 11:
 (9)
(9)
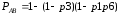 (10)
(10)
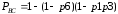 (11)
(11)
Для соединения «звездой» вероятность работоспособности связок А и В, А и С, В и С можно рассчитать по формулам 12, 13, 14:
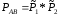 (12)
(12)
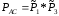 (13)
(13)
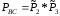 (14)
(14)
Составим систему уравнений:
 (15)
(15)
Разрешив эту
систему относительно
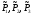 ,
получим:
,
получим:
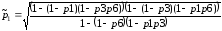 ;
;
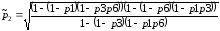 ;
;
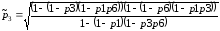 .
.

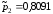

После замены соединения «треугольником» на соединение «звездой» схема упрощается и мы приходим к системе с последовательно-параллельным соединением.
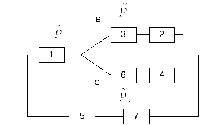
Рисунок 7 – Мостиковая схема после преобразования «треугольник – звезда»
Расчет вероятности новой системы можно посчитать по формуле (16):
 (16)
(16)

Вероятность отказа:

По методу преобразования «треугольник – звезда» получаем маленькое отличие в результате. Дело в том, что метод замены «треугольник – звезда» является приближенным: надежность преобразованной схемы не совпадает с надежностью исходной.
Метод замены «треугольник – звезда» является приближенным методом.
