Второй закон Кеплера (закон площадей)

Второй закон Кеплера.

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

Третий закон Кеплера (гармонический закон)

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет.Справедливо не только для планет, но и для их спутников.

, где и— периоды обращения двух планет вокруг Солнца, аи— длины больших полуосей их орбит.

Ньютонустановил, чтогравитационное притяжениепланеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты:, где— масса Солнца, аи— массы планет.

Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.

22 вопрос

Си́ла Кориоли́са— одна изсил инерции, существующая внеинерциальной системе отсчётаиз-завращенияизаконов инерции, проявляющаяся при движении в направлении под углом к оси вращения.

ричина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. В инерциальных системах отсчётадействуетзакон инерции, то есть, каждое тело стремится двигаться по прямой и с постояннойскоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телуускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса.

Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной , где— кориолисово ускорение. Соответственно, тело действует потретьемузаконуНьютонас силой противоположной направленности.Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другойсилой инерции—центробежной силой, которая направлена порадиусувращающейсяокружности.

Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо.

Физический смысл

Пусть тело движется со скоростью вдоль прямой к центру координат инерциальной системы отсчёта (см. рис.).

Тогда данное движение приведёт к изменению расстояния до центра вращения и, как следствие, абсолютной скорости движения точки неинерциальной системы отсчёта, совпадающей с движущейся точкой — её переносной скорости.

Как мы знаем, эта скорость движения равна

Данное изменение будет равно:

Проведя дифференцирование по времени, получим (направление данного ускорения перпендикулярнои).

С другой стороны, вектор для точки, остающейся неподвижной относительно инерциального пространства, повернётся относительно неинерциального на угол. Или приращение скорости будет

при соответственно второе ускорение будет:

Общее ускорение будет Как видно, система отсчёта не претерпела изменения угловой скоростиЛинейная скорость относительно неё не меняется и остаётсяТем не менее, ускорение не равно нулю.

Если тело движется перпендикулярно направлению к центру вращения, то доказательство будет аналогичным. Ускорение из-за поворота вектора скорости останется а также прибавляется ускорение в результате изменения центростремительного ускорения Пусть тело совершаетсложное движение: движется относительно неинерциальной системы отсчёта S' со скоростьюS' при этом сама движется поступательно с абсолютной линейной скоростьюи одновременно вращается с угловой скоростьюв инерциальной системе координатS.

Тогда линейная скорость тела в неподвижной инерциальной системе координат равна:

, причем

где — радиус-вектор центра масс тела относительно неинерциальной системы отсчетаS'. Продифференцируем данное уравнение:

Найдём значение каждого слагаемого в инерциальной системе координат:

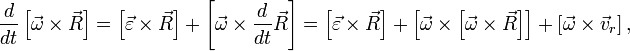
где — линейное ускорение тела относительно системы S' в предположении её неподвижности,— угловое ускорение системы S' .

Таким образом, получаем:

Слагаемое и будеткориолисовым ускорением, образованном от взаимного влияния переносного поворотного и относительного поступательного движений.

Заметим, что если система S также является неинерциальной и движется относительно другой системы, а та другая относительно следующей и т. д., то величины ,для системы S' в последнем уравнении следует считать полными — то есть как сумму собственных ускорений (скоростей) всех систем координат (каждой относительно предыдущей), начиная с первой подвижной системы, а— абсолютным ускорением поступательного движения S' относительно неподвижной инерциальной системы координат.

Заметим также, что в частности, чтобы тело относительно неинерциальной системы отсчета двигалось прямолинейно по радиусу к оси вращения (см. рис.), необходимо приложить к нему силу, которая будет противодействующей суммы Кориолисовой силы , переносной вращательной силыи переносной силы инерции поступательного движения системы отсчета. Составляющая же ускоренияне отклонит тело от этой прямой так как являетсяосестремительным переносным ускорениеми всегда направлена по этой прямой.Действительно, если рассматривать уравнение такого движения, то после компенсации в нём вышеупомянутых сил получится уравнение , которое если умножить векторно на, то с учетомполучим относительнодифур, имеющий при любыхиобщим решением, которое и является уравнением такой прямой —.