Ограничения

С точки зрения статистической физикивторое начало термодинамики имеет статистический характер: оно справедливо для наиболее вероятного поведения системы. Существованиефлуктуацийпрепятствует точному его выполнению, однако вероятность сколь-нибудь значительного нарушения крайне мала. Смотри такжеДемон Максвелла.

Второе начало термодинамики и «тепловая смерть Вселенной»

Клаузиус, рассматривая второе начало термодинамики, пришёл к выводу, что энтропия Вселенной как замкнутой системы стремится к максимуму, и в конце концов во Вселенной закончатся все макроскопические процессы. Это состояние Вселенной получило название «тепловой смерти». С другой стороны, Больцманвысказал мнение, что нынешнее состояние Вселенной — это гигантскаяфлуктуация, из чего следует, что большую часть времени Вселенная все равно пребывает в состоянии термодинамического равновесия («тепловой смерти»)^[3].

По мнению Ландау, ключ к разрешению этого противоречия лежит в областиобщей теории относительности: поскольку Вселенная является системой, находящейся в переменном гравитационном поле, закон возрастания энтропии к ней неприменим^[4].

Поскольку второе начало термодинамики (в формулировке Клаузиуса) основано на предположении о том, что вселенная является замкнутой системой, возможны и другие виды критики этого закона. В соответствии с современными физическими представлениями мы можем говорить лишь о наблюдаемой части вселенной. На данном этапе человечество не имеет возможности доказать ни то, что вселенная есть замкнутая система, ни обратное.

52 Вопрос

Реальный газ—газ, который не описываетсяуравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:

где p — давление; V - объем T — температура; Z_r= Z_r(p,T)  —коэффициент сжимаемостигаза; m - масса; М —молярная масса; R —газовая постоянная.

Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением,объёмомитемпературой.

Для одного молягаза Ван-дер-Ваальса оно имеет вид:

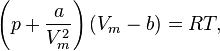
где

• —давление,

• —молярный объём,

• — абсолютнаятемпература,

• —универсальная газовая постоянная.

Видно, что это уравнение фактически является уравнением состояния идеального газас двумя поправками. Поправкаучитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка— объем молекул газа.

Для молей газа Ван-дер-Ваальса уравнение состояния выглядит так:

где—объём,

Таким образом, для частиц внутри сосуда силы притяжения не учитываются. А частицы, находящиеся непосредственно у края сосуда, затягиваются внутрь силой, пропорциональной концентрации:

Число частиц, которые находятся непосредственно у стенок, в свою очередь тоже предполагается пропорциональным концентрации n. Можно считать, что давление на стенки сосуда меньше на некоторую величину, обратно пропорциональную квадрату объёма:

Окончательное уравнение: