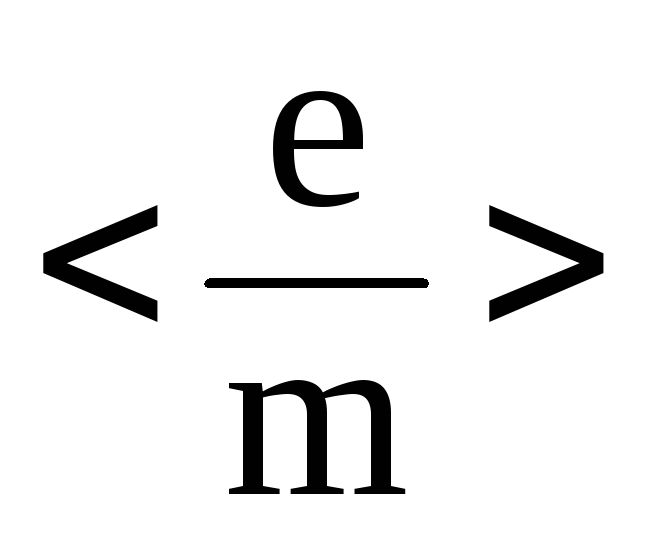Metodychka_201 / Lab7

ЛАБОРАТОРНА РОБОТА № 7

ВИЗНАЧЕННЯ ПИТОМОГО ЗАРЯДУ ЕЛЕКТРОНА

“ МЕТОДОМ МАГНЕТРОНА ”

І. МЕТА РОБОТИ: вивчення дії електричного і магнітного полів на рухомий

електричний заряд та дослідне визначення відношення “методом магнетрона”

ІІ. ДЛЯ РОБОТИ ПОТРІБНІ: електронна лампа з цилінлричним анодом, соленоїд, міліамперметр, вольтметр, амперметр, реостати, джерело напруг типу УИП-1, вимикачі.

ІІІ. ТЕОРЕТИЧНІ ПИТАННЯ ПРОГРАМИ, ЗНАННЯ ЯКИХ

НЕОБХІДНЕ ДЛЯ ВИКОНАННЯ РОБОТИ:

1. Напруженість електричного поля. Поле точкового заряду. Однорідне електричне поле.

2. Сила, що діє на електричний заряд в електричному полі.

3. Сила, що діє на рухомий електричний заряд в магнітному полі.

ІV. ТЕОРЕТИЧНІ ВІДОМОСТІ ТА ОПИС УСТАНОВОК:

1. Заряд електрона е = -1,610^-19 Кл та його маса m= 9,1  10^-31 кг входять до числа фундаментальних сталих фізики. Однак у багатьох фізичних явищах немає потреби визначати абсолютні значення е і m, бо основну роль в них відіграє відношення електрона до його маси, тобто так званий питомий заряд . Знайти цю величину важливо як з теоретичного погляду (зокрема при вивченні внутрішньої будови речовини), так і з практичного (при застосуванні електронно-променевих трубок тощо).

2. Існує багато різноманітних методів визначення відношення . Значна частина їх грунтується на використанні дії електричного і магнітного полів на рухомий електричний заряд.

На заряд q , що рухається зі швидкістю в магнітному полі з індукцією , діє сила Лоренца,

= q[], (7.1)

модуль якої

F=qvBsin (7.2),

де ­­ – кут між векторами і .

Для електрона q=е і тому

= е[] (7.1')

та

F=еvBsin (7.2').

Проте слід звернути увагу на те, що в формулі (7.1') напрямок векторного добутку [] змінюється на протилежний внаслідок його множення на від’ємний заряд електрона .

Якщо  , то sin =1 і тоді сила Лоренца

F=еVB (7.2'').

В загальному випадку, коли на рухомий заряд одночасно діють електричне поле напруженістю та магнітне поле з індукцією , результуюча сила становитиме геометричну суму прискорюючої дії електричного поля е в напрямі – і відхильної дії магнітного поля е[]:

= е+ е[] (7.3)

Строго кажучи „силою Лоренца ” називають силу, визначену за формулою (7.3).

3. Для чіткого розуміння процесів, які мають місце у вакуумних електронних лампах , нагадаємо, що згідно з формулою

= е (7.4)

рух електрона сповільнюється, коли той рухається вздовж силових ліній електричного поля і прискорюється , коли він рухається проти силових ліній цього поля (мал. 7.1):

e

< Мал. 7.1. >

4. Якщо електрон рухається у перпендикулярному манітному полі () , то згідно з векторним добутком (7.1') він відхилявся б у напрямку [] , але від’ємний знак заряду електрона (е<0 ) змінює цей напрямок на протилежний; в підсумку, на електрон діє сила в напрямку е[].

5. Метод вимірювання , застосований у даній роботі називають „ методом магнетрона ” у зв’язку з тим, що застосована тут конфігурація електричного і магнітного полів дуже нагадує конфігурацію полів у магнетронах – генераторах електромагнітних коливань в області надвисоких частот (НВЧ).

Р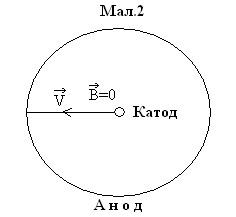ух електронів у цьому випадку відбувається в кільцевому просторі між катодом і анодом двоелектродної електронної лампи.

Нитка розжарення лампи (катод) розташований вздовж осі циліндричного анода. Силові лінії електричного поля спрямовані радіально від додатнього електрода – анода до катода.

При відсутності магнітного поля електрони, що вилітають з катода внаслідок явища термоелектронної емісії , рухаються по прямолінійних траекторіях від катода до анода, тобто вздовж радіусів (мал. 7.2)

Для створення і області між катодом і анодом магнітного поля електронну лампу розташовують так, щоб її нитка розжарення (катод) була віссю соленоїда . Відомо, що соленоїд створює магнітне поле з силовими лініями індукції паралельними його осі. Отже, за такої конструкції установки і будуть взаємно перпендикулярними.

Напруженість електричного поля спрямована по радіусу в напрямку до катода, а індукція магнітного поля паралельна дротині катода лампи. Як видно з формули (1') сила Лоренца завжди перпендикулярна до на-

Рис. 7.2 прямку руху електрона , тому вона не виконує роботи : бо не змінює величини вектора швидкості ; проте вона змінює напрямок вектора .

При деякій достатній величині індукції магнітного поля траєкторія руху електрона перестає вже навіть торкатися анода, тобто електрони не будуть попадати на анод. Отже, критичною індукцією є така індукція магнітного поля, при якій траекторії руху електронів будуть замкненими на катод (мал. 7.3, крива 1). При будь-якій іншій індукції магнітного поля, котра менша від критичної, електрони будуть мати траекторії, що починаються на катоді і закінчуються на аноді (наприклад,

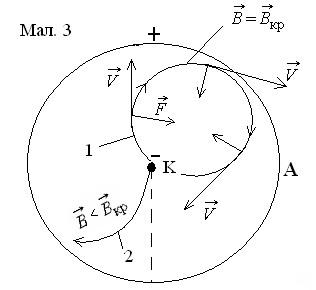крива 2, мал.7.3). Нарешті, із посилен

ням магнітного поля при > згідно

з (7.1') сила, що діє не електрони, буде

зростати і криві (траекторії) руху ефект

ронів будуть дедалі меншого радіуса 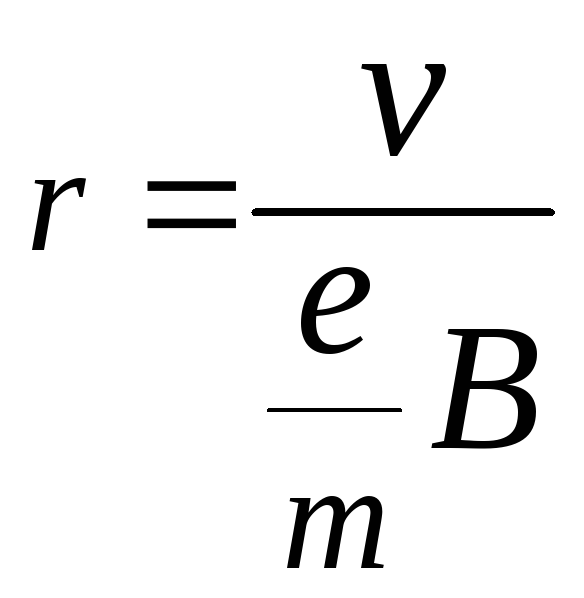(7.5)

Таким чином, сила Лоренца відіграє

роль доцентрової сили

(7.6)

Рис. 7.3 Вважаючи (в першому наближенні), що при =траекторія руху електронів є коловою (мал. 7.3, крива 1) з радіусом , знайдемо з рівності (7.6) шукане відношення:

(7.7)

Швидкість електронів можна визначити з рівності кінетичної енергії електронів, роботи їх прискорення в електричному полі лампи

(7.8)

Тут U_A – різниця потенціалів (напруга) між анодом і катодом. З формули (7.8) : . (7.9)

Підставивши (7.9) у (7.7), одержимо:

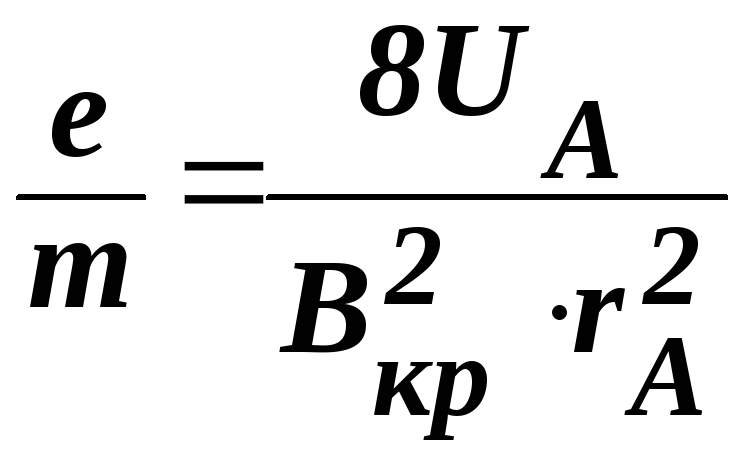. (7.10)

Крива залежності струму в електронній лампі від індукції магнітного поля при сталому струмі розжарення катода і сталій анодній напрузі U_A в ідеальному випадку виражається пунктирною кривою 1 (мал. 7.4).

В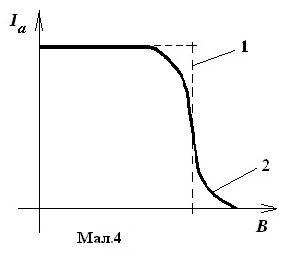наслідок того, що електрони, які рухаються від катода до анода, мають різні швидкості, зменшення анодного струму відбувається поступово

(крива 2 на мал. 4); повільніші електрони перестають попадати на анод при меншому значенні індукції магнітного поля , ніж більш швидкі.

Якщо знімати криві І _а = f(B) при різних значеннях анодної напруги U_A, одержимо сім’ю кривих для різних .

Рис. 7.4 Однак, при знятті цих кривих напруга розжарення катода повинна бути однаковою. Криві І _а = f(B) ще називають скидними характеристиками лампи.

У даній роботі замість діодів з циліндричним анодом можна використовувати тріод з таким самим анодом, наприклад, лампу 6С5С. Щоб третій електрод тріода – сітка не спотворювала результатів вимірювання , її сполучають з анодом через великий опір (десятки тисяч омів). Як уже згадувалось вище, магнітне поле створюється за допомогою соленоїда , довжини якого значно більша діаметра. Тоді можна вважати, що в середній частині соленоїда магнітне поле буде однорідним, а його індукцію знаходять за формулою:

, (7.11)

де μ – відносна магнітна проникність середовища (в нашому випадку повітря);

μ₀ – магнітна стала , якою називають абсолютну магнітну проникність вакууму

( );

І_с – сила стуму в обмотці соленоїда ( в амперах);

n – чисо витків, що припадають на одницю довжини соленоїда (для даного соленоїда n=8·10³ ).

Соленоїд живиться від джерела постійного струму , наприклад, ВСА-5К.

Струм в соленоїді будемо вважати критичним І_кр при В=В_кр . Тоді врахувавши (7.11). Остаточно одержимо таку робочу формулу:

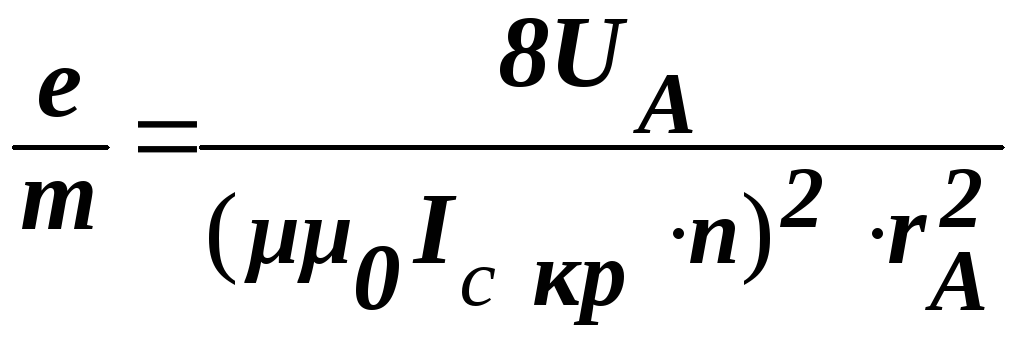(7.12)

Отже, для визначення питомого заряду електрона „методом магнетрона”, необхідно знати радіус r_A анода лампи (для даної лампи r_A=9,6 мм), число витків соленоїда n на одиницю довжини, анодну напругу U_A та I_{c кр} , що знаходиться з I_A = f( I_c) , подібного до графіка I_A = f(В), наведенного на мал. 7.4.

V. ЗАВДАННЯ ТА ХІД ЙОГО ВИКОНАННЯ

Визначити питомий заряд електрона

1. Збирають установку за схемою, поданою на рис.7.5.

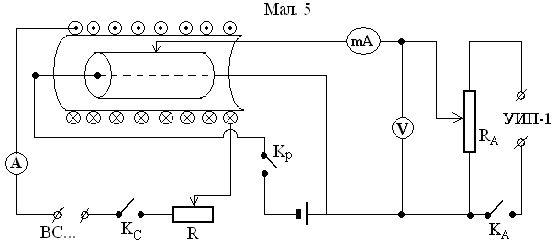
Рис. 7.5

2. Ставлять контакт потенціометра R_A в положення, при якому U_A = 0 і вмикають коло розжарення.

3. Замикають коло анода (ключем К_Р) і за допомогою потенціометра R_A установлюють одну з напруг U_A , наприклад, 100 В і переконуються в тому, що величина анодного струму припадає на другу половину шкали міліамперметра.

4. Увімкнувши максимальний опір R , замикають коло соленоїда (ключа К_С) і міліамперметром вимірюють силу анодного струму.

5. Збільшують силу струму в соленоїді І_С в межах від 0 до максимального і вимірюють залежність I_а = f( I_С ) . Дані заносять у таблицю 7.1.

Таблиця 7.1

ІС, А	0	0,1	0,2	0,3	………
Іа, мА
∆ Іа, мА

IC , А	0	0,1	0,2	0,3	..........
Іа , мА
∆ Іа , мА

6. Ставлять R_С у вихідне положення , при якому І_С = 0, розмикають коло соленоїда і повторюють вимірювання при інших значеннях анодної напруги U_A . Дані заносять у таблиці 7.1, 7.1', 7.2'' ..., аналогічні таблиці 7.1'.

7. За даними таблиць 7.1, 7.1', 7.2'', ... будують скидні характеристики при різних U_A , з яких методом диференціювання кривої знаходять залежності ∆І_А = f( I_C), їх будують на фоні скидних характеристик.

8. За максимумами залежностей ∆І_А = f( I_C) з графіків визначають І_{с кр} , І'_{С кр}, І''_{С кр} ... . Дані заносять у таблицю 7.2

9. Для кожного рядка таблиці 2 розраховують за формулою (7.12) і проводять статистичну обробку даних за програмою 1 (додатки 2 і 3).

10. Записують остаточний результат:

=

і роблять висновок про якість проведених вимірювань (наприклад, на скільки % відрізняється одержаний результат від табличного значення –

Таблиця 7.2

№ п/п	UА	ІІскр	р	и	t, n		S<>		E
	В	А	м						%
1. 2. 3. …

VI. ЛІТЕРАТУРА

[1] – стор. 331, 336–337, 396–401. [5] – стор. 312–316, 368–378.

[2] – стор. 13–17, 161–165. [7] – стор. 184–189.

[3] – стор. 16–20, 208–217. [8] – стор. 321–324.

[4] – стор. 116–118, 223–225. [9] – стор. 96–99.

.

VII. ЗАПИТАННЯ ДЛЯ САМОКОНТРОЛЮ І КОНТРОЛЮ

1.За законом збереження енергія замкненої системи зберігається.А у яких випад-

ках енергія системи змінюється? Яка причина зміни кінетичної енергії заряду,що

рухається в електростатичному полі?

2.Чи змінюється енергія заряду, який влітає у магнітне поле:

–вздовж силових ліній цього поля?

–перпендикулярно до силових ліній магнітного поля? Поясніть відповідь.

3.Дайте визначення основного закону динаміки обертального руху. Зробіть малю-

нок, на якому зазначте напрямки векторів моменту імпульсу електрона, що руха-

ється по колу в магнітному полі, та моменту сили Лоренца.

4.Як треба змінити описаний у цій роботі метод для визначення відношення заря-

ду до маси для протона? Чи можна застосовувати цей метод для визначення хара-

ктеристик нейтрона? Відповідь обґрунтуйте.

5.Як рухається електричний заряд в однорідному магнітному полі, коли кут між

напрямком вектора швидкості заряду і напрямком вектора магнітної індукції до-

рівнює: 0; /2; довільній величині?

6.Пояснити принцип дії магнетрона.

7.Намалювати траєкторії руху електрона у магнітному полі для випадків:

1) В < В_кр ; 2) В = В_кр; 3) В > В_кр.