
Тема лінійна алгебра засобами ms excel, застосування у задачах економіки
Засоби MS Excel виявляються корисними в лінійній алгебрі, перш за все, для операцій з матрицями. Для роботи з матрицями використовують різні функції MS Excel.
Матриця – це числовий масив з певною кількістю рядків та стовпців. Матриці можна перемножувати між собою, множити на вектор, множити на число, створювати обернені матриці тощо.
Робота з матрицями
Знаходження оберненої матриці
У MS Excel для знаходження оберненої матриці використовується функція МОБР, яка обчислює обернену матрицю для матриці, що зберігається в таблиці у вигляді масиву.
Функція МОБР має синтаксис:
МОБР (масив), де масив – це числовий масив з рівною кількістю рядків і стовпців. Масив може бути заданий як діапазон комірок, наприклад А1:СЗ; як масив констант, наприклад {1,2,3:4,5,6:7,8,9} або як ім’я діапазону або масиву.
Комп’ютерна технологія знаходження оберненої матриці:
Розв’язання задачі у системі MS Excel реалізується у такий спосіб:
Спочатку треба створити матрицю
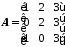 в
діапазоні комірокА2:С4
(рис. 3
1.),
в
діапазоні комірокА2:С4
(рис. 3
1.),

Рис. 3.1.
Після цього над елементами матриці можна виконувати різні дії. Необхідно отримати обернену матрицю.
Виділити блок вільних комірок під обернену матрицю. Наприклад, блок комірок А6:С8.
Вибрати меню Вставка – Функция (рис. 3.2.)

Рис. 3.2.
Або натиснути на панелі інструментів Стандартная кнопку Вставка функции.
У результаті виконаних дій з’являється діалогове вікно Мастер функций. На першому кроці майстра функцій вибрати категорію Математические і далі вибрати функцію МОБР (Рис. 3.3.), після чого натиснути кнопку ОК.

Рис.3.3.
У вікні Аргументы функции текстового поля Массив задати область, від якої необхідно знайти обернену матрицю, тобто А2:С4 після чого одночасно натиснути три клавіші Ctrl+Shift+Enter (Рис. 3.4.):
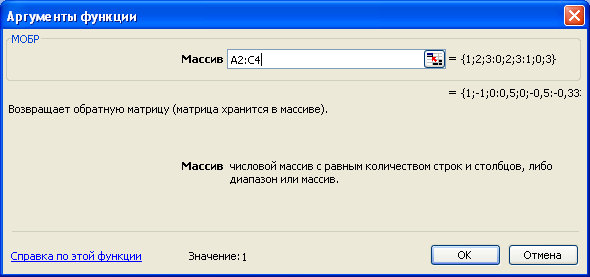
Рис. 3.4.
У діапазоні комірок А6:С8 з’явиться результат обчислення оберненої матриці (рис. 3.5.):

Рис. 3.5.
Множення матриць
У MS Excel для множення матриць використовується функція МУМНОЖ (матриці зберігаються в масивах).
Функція МУМНОЖ має синтаксис:
МУМНОЖ (массив 1;массив 2), де массив 1, массив 2 – це масиви, які треба перемножити. При цьому кількість стовпців аргументу массив 1 повинна бути саме такою, як кількість рядків аргументу массив 2, і обидва масиви повинні містити тільки числа. Результатом множення матриць є масив з таким же числом рядків, як массив 1 і з таким же числом стовпців, як массив 2.
Комп’ютерна технологія множення матриць:
Розв’язання задачі у системі MS Excel реалізується у такий спосіб:
1.
Перемножити матрицю 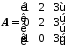 та матрицю
та матрицю .
Матриця А
введена в діапазон комірок А2:С4,
а матриця
В
– в діапазон комірок А6:С8
(Рис. 3.6.).
.
Матриця А
введена в діапазон комірок А2:С4,
а матриця
В
– в діапазон комірок А6:С8
(Рис. 3.6.).
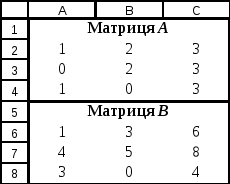
Рис. 3.6.
Виділити блок вільних комірок для отримання результату від множення матриць. Наприклад, блок комірок А10:С12. Розмір вільних комірок відповідає заданим матрицям.
Вибрати меню Вставка – Функция (Рис. 3.2.). Або натиснути на панелі інструментів Стандартная кнопку Вставка функции.
У результаті виконаних дій з’являється діалогове вікно Мастер функций. На першому кроці майстра функцій вибрати категорію Математические і далі вибрати функцію МУМНОЖ (Рис. 3.7.), після чого натиснути кнопку ОК.
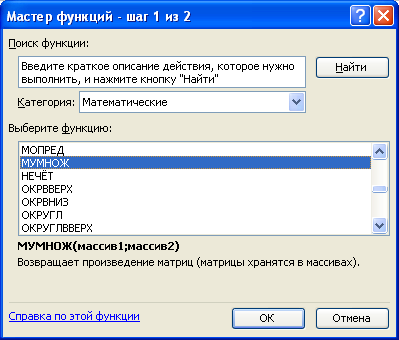
Рис. 3.7.
У вікні Аргументы функции до текстового поля Массив1 ввести діапазон матриці А – А2:С4, до текстового поля Массив2 ввести діапазон матриці В – А6:С8 (Рис. 3.8.), після чого одночасно натиснути три клавіші Ctrl+Shift+Enter.

Рис. 3.8.
У діапазоні комірок А10:С12 з’явиться результат множення матриці А на матрицю В (Рис. 3.9.).

Рис. 3.9.
Множення матриці на вектор
У MS Excel для множення матриць використовується функція МУМНОЖ.
Функція МУМНОЖ має синтаксис:
МУМНОЖ (массив 1;массив 2), де массив 1, массив 2 – це масиви, які треба перемножити. Кількість стовпців аргументу массив 1 має бути саме такою, як і кількість рядків аргументу массив 2. Результатом множення матриць є масив з таким же числом рядків, як массив 1 і з таким же числом стовпців, як массив 2.
Комп’ютерна технологія множення матриці на вектор:
Розв’язання задачі у системі MS Excel реалізується у такий спосіб:
Перемножити початкову матрицю
 та векторС.
Для цього матрицю А
введіть у діапазон комірок А2:С4,
а вектор С
(вектор С
повинен мати стільки рядків, скільки
стовпців є в матриці)
– в діапазон комірок Е2:Е4
(Рис. 3.10.).
та векторС.
Для цього матрицю А
введіть у діапазон комірок А2:С4,
а вектор С
(вектор С
повинен мати стільки рядків, скільки
стовпців є в матриці)
– в діапазон комірок Е2:Е4
(Рис. 3.10.).
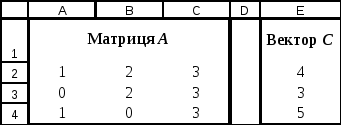
Рис. 3.10.
Виділити блок вільних комірок для отримання результату, де буде створюватися нова матриця. Наприклад, блок комірок G2:I4. Розмір вільних комірок повинен відповідати розміру матриці А.
Вибрати меню Вставка – Функция (Рис. 3.2.). Або натиснути на панелі інструментів Стандартная кнопку Вставка функции.
У результаті виконаних дій з’являється діалогове вікно Мастер функций. На першому кроці майстра функцій вибрати категорію Математические і далі вибрати функцію МУМН0Ж (Рис. 3.7.), після чого натиснути кнопку ОК.
У вікні Аргументы функции до текстового поля Массив1 ввести діапазон матриці А – А2:С4, до текстового поля Массив2 ввести діапазон вектора С – Е2:Е4 (Рис. 3.11.), після чого одночасно натиснути три клавіші Ctrl+Shift+Enter.

Рис. 3.11.
У діапазоні комірок G2:I4 з’явиться результат множення початкової матриці А на вектор С (Рис. 3.12.).
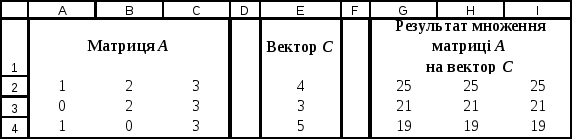
Рис. 3.12.
Множення матриці на число
У MS Excel для виконання операцій складання і віднімання матриць можуть бути використані формули, що вводяться у відповідні комірки.
Комп’ютерна технологія множення матриці на число:
Розв’язання задачі у системі MS Excel реалізується у такий спосіб:
Треба перемножити матрицю
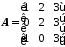 на
число 3.
на
число 3.
Для цього треба виділите блок вільних комірок, наприклад А6:С8, для отримання результату від множення матриці А на число 3, та занести формулу =A2:C4*3. Розмір вільних комірок повинен відповідати заданій матриці А.
Далі одночасно необхідно натискнути три клавіші Ctrl+Shift+Enter. У діапазоні комірок А6:C8 з’явиться результат множення матриці А на число 3 (Рис. 3.13.).

Рис. 3.13.
Додавання і віднімання матриць
У MS Excel для виконання операцій додавання і віднімання матриць можуть бути використані формули, що вводяться у відповідні комірки.
Комп’ютерна технологія складання і віднімання матриць:
Розв’язання задачі у системі MS Excel реалізується таким чином:
Необхідно знайти матрицю С, що є сумою матриць А, В. Матриця
 введена
в діапазон комірок А2:С3,
а матриця
введена
в діапазон комірок А2:С3,
а матриця
 введена
в
діапазон комірок
А5:С6
(рис. 3.14.).
введена
в
діапазон комірок
А5:С6
(рис. 3.14.).

Рис. 3.14.
Треба обчислити у діапазоні комірок А8:C9 суму матриць (А+В). Для цього потрібно виділити блок вільних комірок А8:C9 для отримання результату та занести формулу =А2:С3+ А5:С6. Розмір вільних комірок повинен відповідати розміру заданих матриць.
Далі одночасно необхідно натискнути три клавіші Ctrl+Shift+Enter. У діапазоні комірок А8:C9 з’явиться результат обчислення суми матриць А, В (рис. 3.15.).
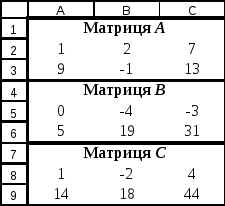
Рис. 3.15.
Подібним же чином обчислюється різниця матриць А, В, тільки у формулі для обчислення першого елементу замість знаку + ставиться знак –. Необхідно знайти матрицю D, що є різницею матриць А, В. Результат обчислення різниці матриць А, В (рис. 3.16.).
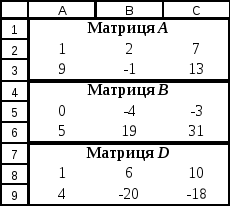
Рис. 3.16
Транспонування матриць
Для здійснення транспонування в MS Excel використовується функція ТРАНСП. Функція ТРАНСП дозволяє переводити вертикальний діапазон комірок у горизонтальний і навпаки на робочому листі.
Функція ТРАНСП має синтаксис:
ТРАНСП (массив),
де масив – це масив, що транспонується, або діапазон комірок на робочому листі. Транспонування масиву полягає в тому, що перший рядок масиву стає першим стовпцем нового масиву, другий рядок масиву стає другим стовпцем нового масиву і т.д.
Комп’ютерна технологія транспонування матриць:
Розв’язання задачі у системі MS Excel реалізується таким чином:
Необхідно створити транспоновану матрицю з елементів матриці А. Матриця A =
 введена в діапазон комірок А2:Е3
розміром 2 x 5 (рис. 3.17.).
введена в діапазон комірок А2:Е3
розміром 2 x 5 (рис. 3.17.).

Рис. 3.17.
Треба виділити блок вільних комірок А6:В10 під транспоновану матрицю (5 х 2).
Вибрати меню Вставка – Функция (Рис. 3.2.) або натиснути на панелі інструментів Стандартная кнопку Вставка функции.
У результаті виконаних дій з’являється діалогове вікно Мастер функций. На першому кроці майстра функцій вибрати категорію Ссылки и массивы і далі вибрати функцію ТРАНСП (рис. 3.18.), після чого натиснути кнопку ОК.
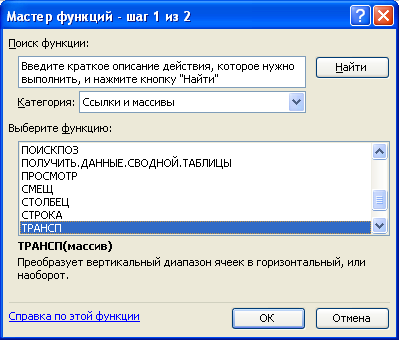
Рис. 3.18.
У вікні Аргументы функции до текстового поля Массив ввсти діапазон матриці А – А2:Е3 (рис. 3.19.), після чого одночасно натиснути три клавіші Ctrl+Shift+Enter.

Рис. 3.19.
У діапазоні комірок А6:В10 з’явиться транспонована матриця з елементів матриці А (рис. 3.20.).
Якщо транспонована матриця не з’явилася в діапазоні А6:В10, то слід клацнути покажчиком миші в рядку формул та повторити натиснення комбінації клавіш Ctrl+Shift+Enter.
У результаті в діапазоні комірок А6:В10 з’явиться транспонована матриця з елементів матриці А (рис. 3.20.).

Рис. 3.20.
Обчислення визначника матриці
У MS Excel для обчислення визначника квадратної матриці використовується функція МОПРЕД.
Функція МОПРЕД має синтаксис:
МОПРЕД (массив),
де массив – це числовий масив, в якому зберігається матриця з рівною кількістю рядків і стовпців.
Комп’ютерна технологія обчислення визначника матриці:
Розв’язання задачі у системі MS Excel реалізується такими діями:
Необхідно обчислити визначник матриці
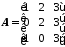 .
МатрицяА
введена
в діапазон комірок А2:С4
(рис. 3.21.).
.
МатрицяА
введена
в діапазон комірок А2:С4
(рис. 3.21.).

Рис. 3.21.
Табличний курсор треба поставити в комірку, в якій потрібно набути значення визначника, наприклад в Е2.
Вибрати меню Вставка – Функция (рис. 3.2.) або натиснути на панелі інструментів Стандартная кнопку Вставка функции.
У результаті виконаних дій з’являється діалогове вікно Мастер функций. На першому кроці майстра функцій требавибрати категорію Математические і далі вибрати функцію МОПРЕД (рис. 3.22.), після чого натиснути кнопку ОК.
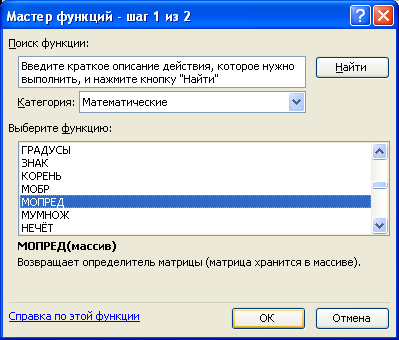
Рис. 3.22.
У вікні Аргументы функции до текстового поля Массив ввести діапазон матриці А – А2:С4 (рис. 3.23.), після чого натиснути комбінацію клавіш Ctrl+Shift+Enter.
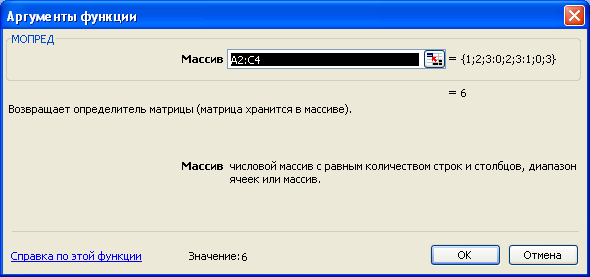
Рис. 3.23.
В результаті у комірці Е2 з’явиться значення визначника матриці А – 6. (рис. 3.24.).

Рис. 3.24.
