
- •Аналітична геометрія у просторі.
- •Тема 1 : Площина. Види рівнянь.
- •Рівняння площини „у відрізках”
- •Рівняння площини, що проходить через три точки.
- •Розв'язок типових задач.
- •Тема 2. Взаємне розміщення площин.
- •Відстань від точки до площини.
- •Кут між площинами. Умова паралельності й перпендикулярності площин.
- •Розв'язок типових задач.
- •Тема 3. Деякі задачі на пряму і площину в просторі.
- •Кут між прямою та площиною
- •Перетин прямої з площиною
- •Рівняння прямої, яка проходить через точку перпендикулярно до даної площини
- •Рівняння площини, яка проходить через точку паралельно до заданої площини
- •Рівняння площини, що проходить через дану точку перпендикулярно до заданої прямої.
Аналітична геометрія у просторі.
Тема 1 : Площина. Види рівнянь.
Зміст:
Загальне рівняння площини. Рівняння площини, що проходить через відому точку і перпендикулярна до заданого вектора.
Рівняння площини „у відрізках”.
Рівняння площини, що проходить через три точки.
Нормальне рівняння площини.
Розв'язок типових задач.
Загальне рівняння площини. Рівняння площини, що проходить через відому точку і перпендикулярна до заданого вектора
Нехай задані де вартова система координат
Охуz і
рівняння першого степеня![]() .
.
Тоді справедлива теорема:
Теорема: Кожна площина може бути виражена лінійним рівнянням відносно вибраної декартової системи координат у просторі і навпаки, кожне лінійне рівняння відносно декартової системи координат у просторі виражає площину.
Іншими словами – площина є єдиною поверхнею першого порядку.
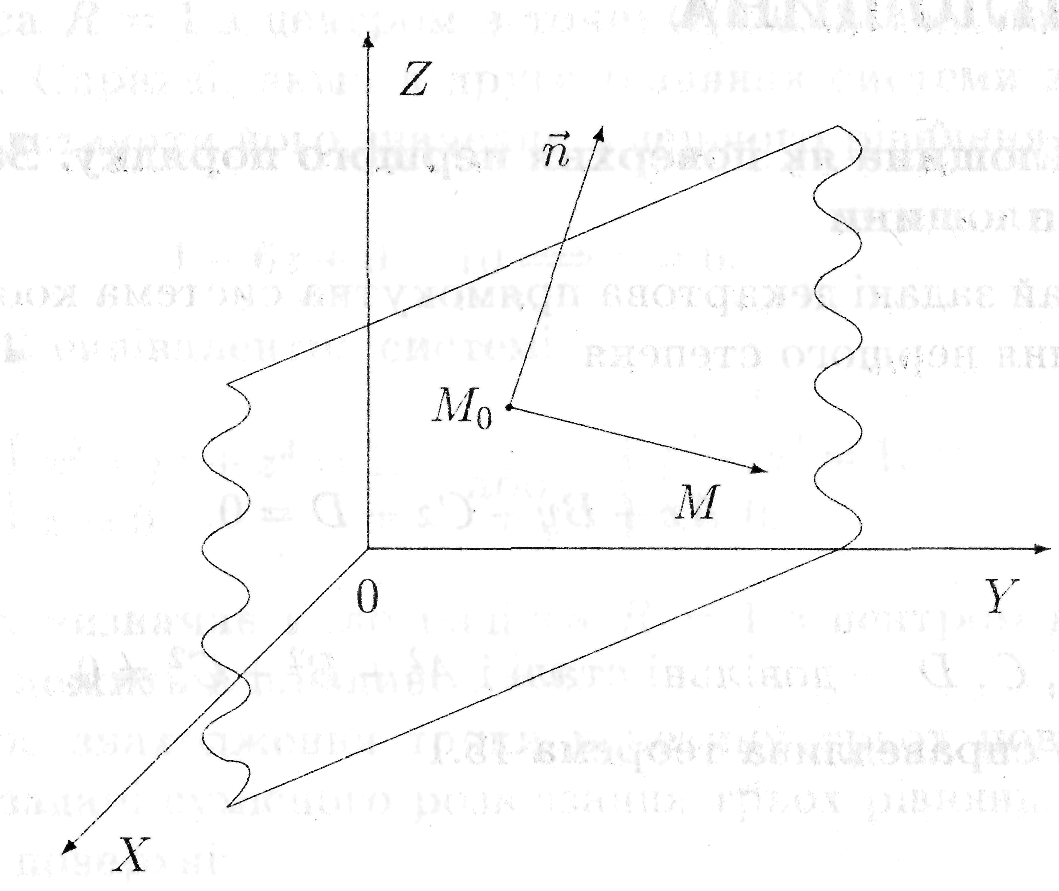 Дійсно,
нехай
Дійсно,
нехай![]() - довільна площина;
- довільна площина;
![]() -
одна з її точок;
-
одна з її точок;
![]() -
перпендикулярний до неї вектор;
-
перпендикулярний до неї вектор;
Тоді, якщо точка
![]() належить площині
належить площині![]() ,
то вектори
,
то вектори![]() і
і![]() будуть перпендикулярні.
будуть перпендикулярні.
Це позначає, що скалярний добуток даних векторів дорівнює нулю. Тобто:
![]() (1)–рівняння площини у
векторній формі.
(1)–рівняння площини у
векторній формі.
Виведемо рівняння площини, що проходить через задану точку і перпендикулярно для заданого вектора в координатній формі:
Перпендикулярність векторів
![]() і
і![]() в координатній формі позначає:
в координатній формі позначає:
![]() -(2) - рівняння шуканої прямої в
координатній формі
-(2) - рівняння шуканої прямої в
координатній формі
Розкриємо дужки :
![]() і позначивши через
і позначивши через![]() отримаємо загальне рівняння площини:
отримаємо загальне рівняння площини:
![]() (3) - рівняння площини в загальному
вигляд, де
(3) - рівняння площини в загальному
вигляд, де ![]() - векторїї нормалі або нормальний
вектор
- векторїї нормалі або нормальний
вектор
Рівняння площини „у відрізках”
Якщо всі коефіцієнти А, В, С і Dто загальне рівняння(3) можна записати у вигляді:
 і позначимо через
і позначимо через![]() .
.
Тоді рівняння площини прийме вигляд:
![]() (4)
(4)
Розглянемо геометричний зміст чисел a, b, c:
Знайдемо точки перетину даної площини з координатними осями:
Ох:
![]() .
Рівняння приймає вигляд:
.
Рівняння приймає вигляд:![]() .
Тобто точка
.
Тобто точка![]()
Оу:
![]() Рівняння приймає вигляд:
Рівняння приймає вигляд:![]() .
Тобто точка
.
Тобто точка![]()
Oz: ![]() Рівняння приймає вигляд:
Рівняння приймає вигляд:![]() .
Тобто точка
.
Тобто точка![]()
Отже, точки
![]() ,
,![]() ,
,![]() - шукані точки перетину площини з
координатними віссями, причому числаa, b,
c – величини
відрізків, які відтинає площина на осях
Ох, Оу, Оz.
- шукані точки перетину площини з
координатними віссями, причому числаa, b,
c – величини
відрізків, які відтинає площина на осях
Ох, Оу, Оz.
Тому, рівняння(4)називають рівнянням площини у «відрізках»
Приклад: Знайти
точки перетину площини![]() з осями координат.
з осями координат.
Розв'язання:
Запишемо дане рівняння площини у «відрізках». Для цього поділимо ліву і праву на вільний член - 24:

Отже, дана площина перетинає
координатні вісі Ох, Оу, Оzвідповідно у точках![]() ,
,![]() ,
,![]()
Рівняння площини, що проходить через три точки.
З курсу геометрії відомо, що площину однозначно можливо задати трьома точками.
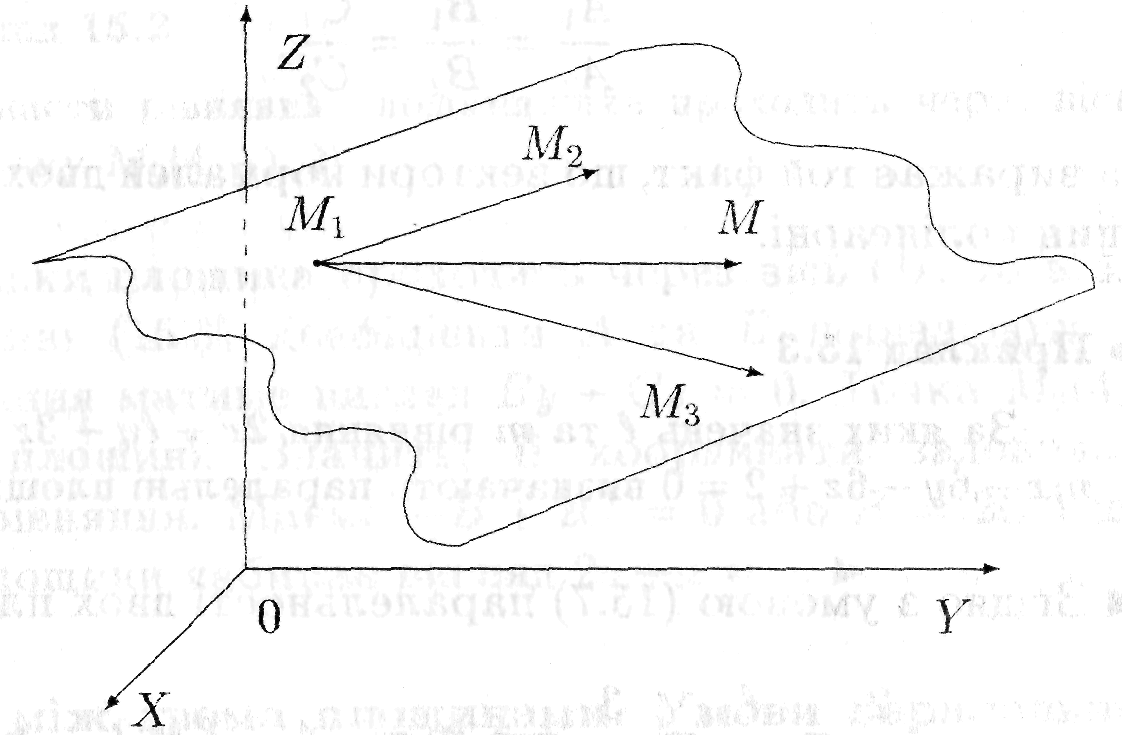 Отже, нехай площина задана трьома своїми
точками,
Отже, нехай площина задана трьома своїми
точками,![]()
![]() ,
,![]() ,
які не лежать на одній прямій. Точка
,
які не лежать на одній прямій. Точка![]() - довільна точка шуканої площини. Тоді,
вектори
- довільна точка шуканої площини. Тоді,
вектори![]() - компланарні вектори, а тому їх мішаний
добуток дорівнює нулю. В векторній
формі, це має вигляд:
- компланарні вектори, а тому їх мішаний
добуток дорівнює нулю. В векторній
формі, це має вигляд:![]() або в координатній формі:
або в координатній формі:
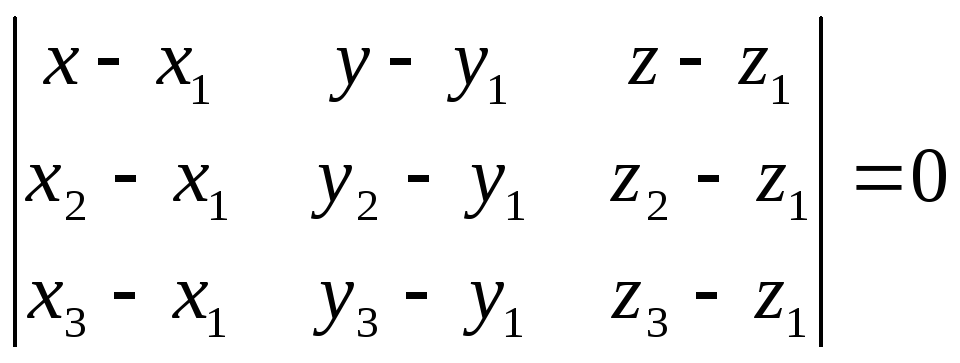 (5) – рівняння площини, що проходить
через три точки.
(5) – рівняння площини, що проходить
через три точки.
Приклад: Скласти рівняння площини,
що проходить через точки![]() ,
,![]()
![]() .
.
Розв'язання:
Нехай,
![]() - довільна точка шуканої площини. За
рівнянням(5) маємо:
- довільна точка шуканої площини. За
рівнянням(5) маємо:
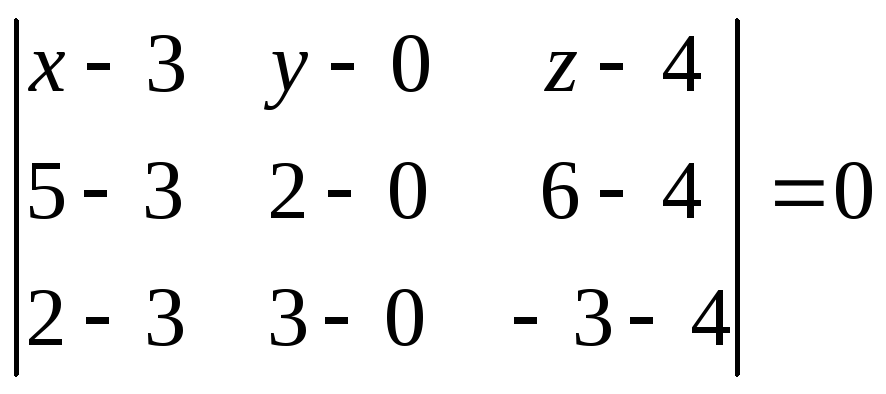 або
або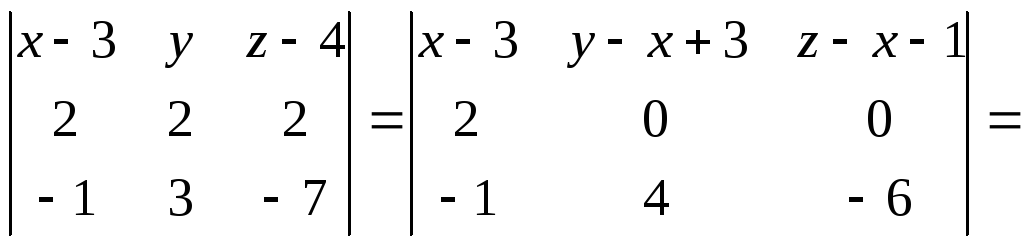

Отже, шукане рівняння площини, яка проходить через три задані точки має вигляд:
![]() .
.
Відповідь:
![]()
Нормальне рівняння площини
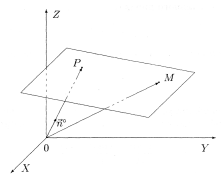 Нехай
в просторі задана площина
Нехай
в просторі задана площина![]() ,
яка визначається відстанню р від початку
координат, тобто -
,
яка визначається відстанню р від початку
координат, тобто -![]() - довжиною перпендикуляра, опущеного з
початку координат на площину, і напрямом
цього перпендикуляра, тобто кутами
- довжиною перпендикуляра, опущеного з
початку координат на площину, і напрямом
цього перпендикуляра, тобто кутами![]() ,
які він утворює з додатними напрямами
осей системи координат. Одиничний вектор
нормалі даної площини буде мати координати
,
які він утворює з додатними напрямами
осей системи координат. Одиничний вектор
нормалі даної площини буде мати координати
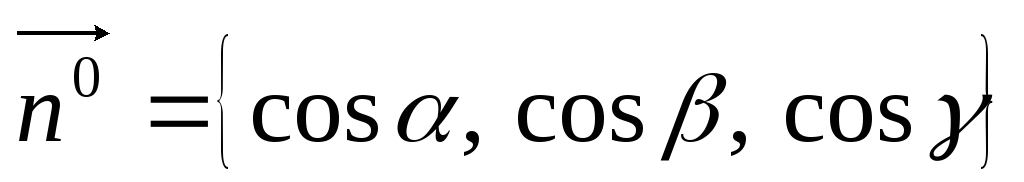 ;
; - довільна точка шуканої площини.
- довільна точка шуканої площини.Знайдемо проекцію вектора
 на вектор нормалі площини, на вектор
на вектор нормалі площини, на вектор :
:
![]() .
З іншого боку
.
З іншого боку![]()
![]() .
.
Порівнюючи два останніх вирази можемо записати для проекції вектора рівняння
![]() (6) – нормальне рівняння площини в
векторній формі
(6) – нормальне рівняння площини в
векторній формі
![]() (7)–нормальне рівняння площини
в координатній формі
(7)–нормальне рівняння площини
в координатній формі
Алгоритм зведення загального рівняння площини до нормального:
Потрібно помножити всі коефіцієнти загального рівняння площини
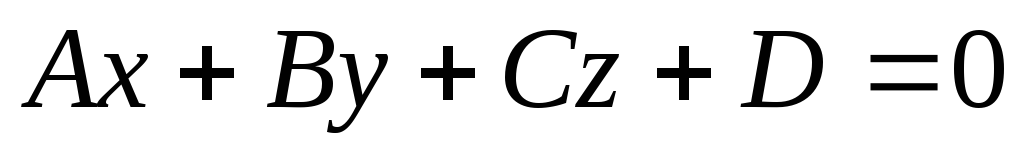 на множник
на множник (нормувальний множник рівняння);
(нормувальний множник рівняння);Знак нормувального множника вибрати так, щоб він був протилежний до вільного члена рівняння площини D.
Загальне рівняння прийме вигляд:
 (8), яке називаєтьсянормальним
рівнянням площини.
(8), яке називаєтьсянормальним
рівнянням площини.
Приклад: Звести до нормального вигляду
рівняння площини
![]() .
.
Розв'язання:
За алгоритмом і формулою (8)можемо
записати:![]()
![]()
Отже,
![]() - шукане рівняння площини, де
- шукане рівняння площини, де![]()
