Практична робота № 2. Редукування трикутника тріангуляції з поверхні Землі на поверхню референц-еліпсоїда.
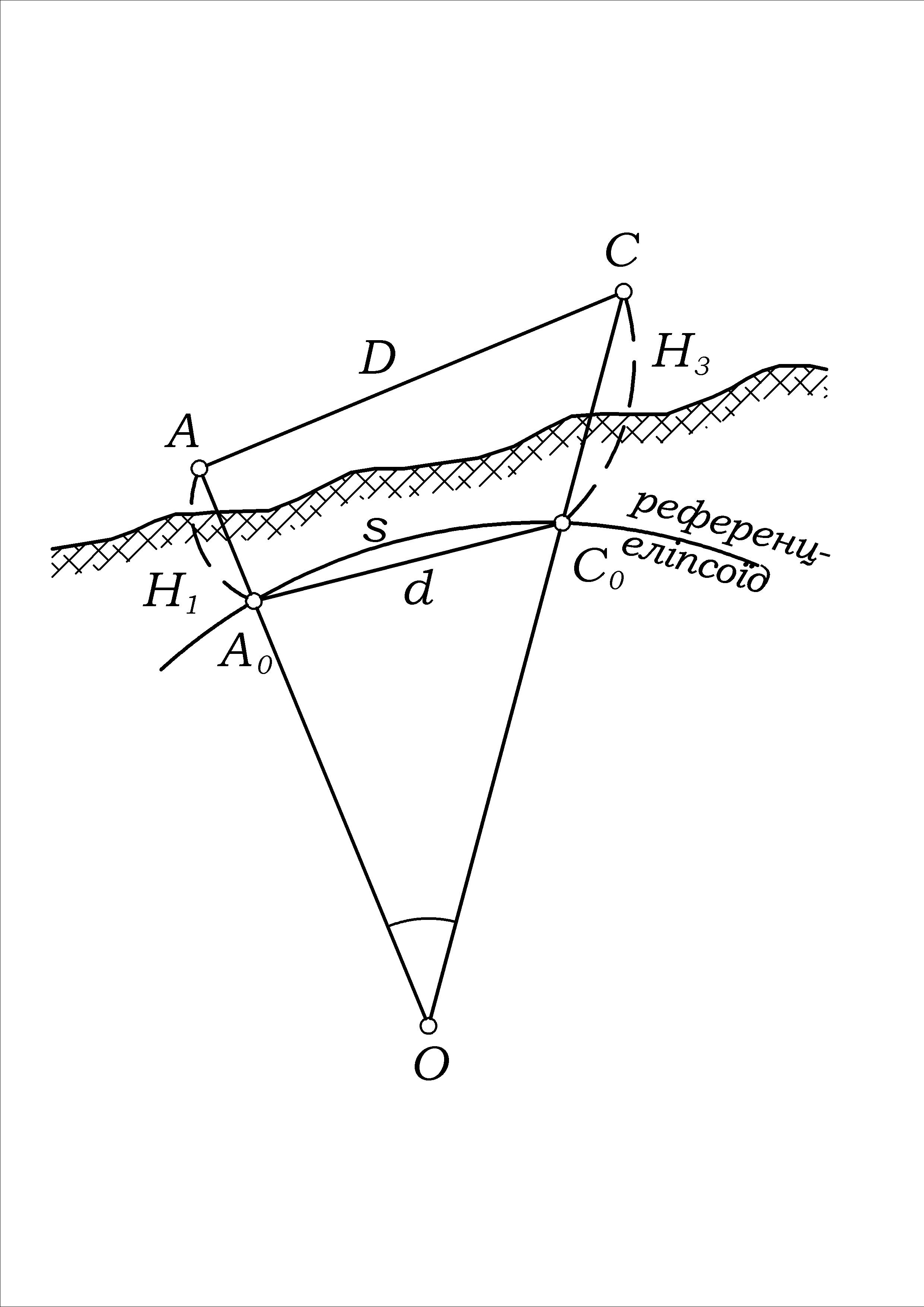
Виміряні на поверхні Землі елементи геодезичної мережі (довжини сторін, горизонтальні напрямки та вертикальні кути, прискорення сили ваги) редукують на поверхню прийнятого референц-еліпсоїда по нормалях (згідно методу проектування, запропонованого проф. Красовським). Теорію переходу від виміряних на земній поверхні величин до відповідних їм величин на поверхні референц-еліпсоїда називають редукційною задачею геодезії.
|
|
|
|
а – редукція лінійних вимірів |
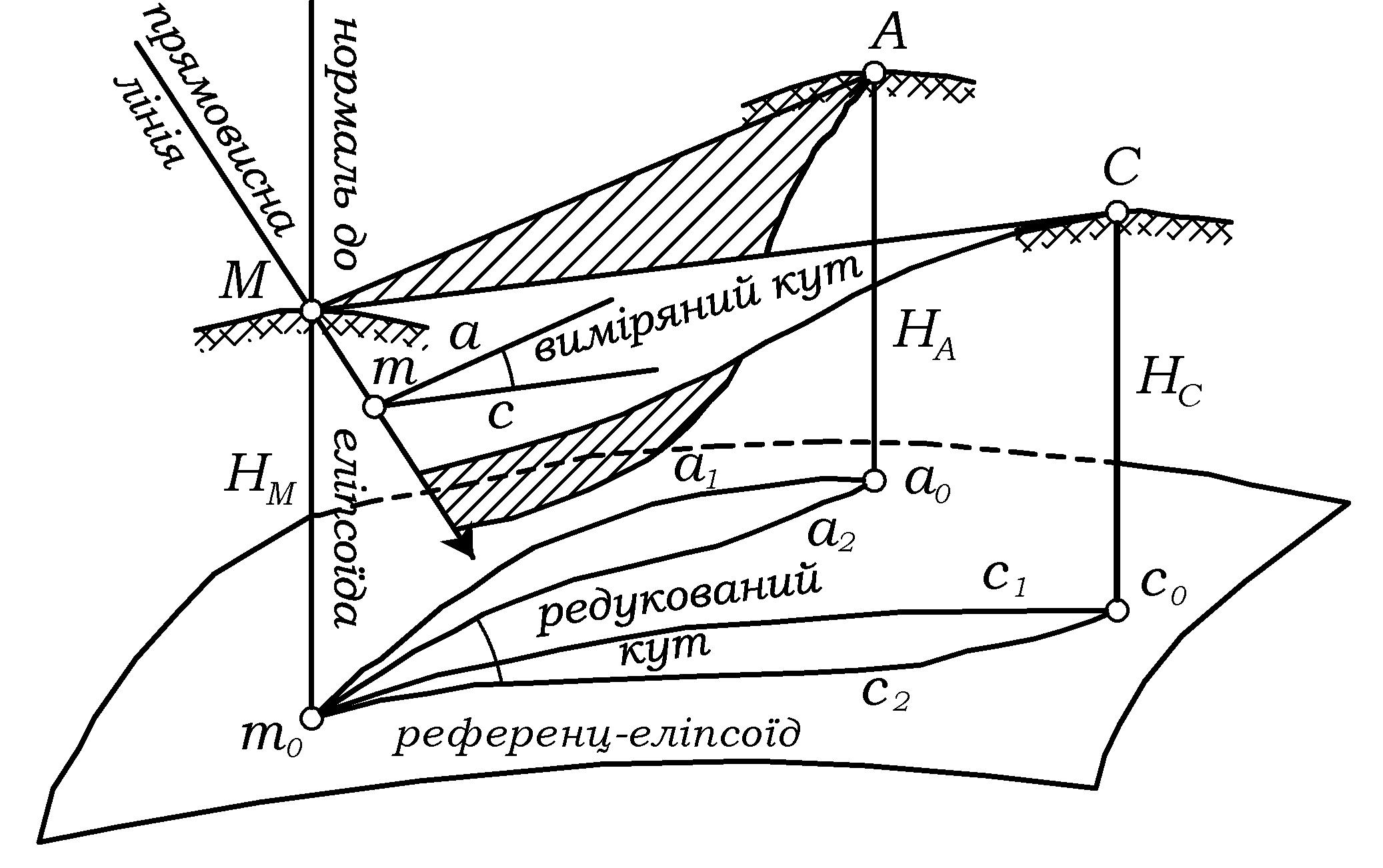
б – редукція горизонтальних напрямків |
|
Рис.2 Редукція елементів трикутника тріангуляції з поверхні Землі на поверхню референц-еліпсоїда. |
|
Розв’язуючи дану задачу, необхідно виконати наступні дії:
-
Редукування довжини сторони трикутника – виміряної похилої віддалі
між пунктами
і
земної поверхні на поверхню
референц-еліпсоїда по нормалях (рис.2,
а):-
Обчислення довжини хорди
,
що з’єднує точки
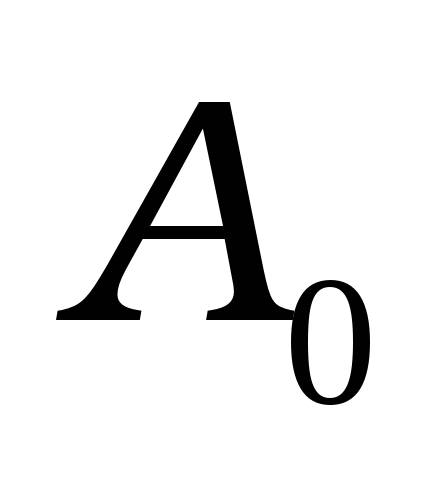і
–
проекції точок
і
на поверхню референц-еліпсоїда. -
Перехід від хорди
до довжини дуги
на поверхні референц-еліпсоїда.
-
-
Редукування виміряних кутів. У кожний виміряний на земній поверхні горизонтальний напрям, попередньо приведений до центрів знаків, повинні бути введені наступні поправки:
-
Поправка за перехід від прямовисної лінії, по якій встановлюються геодезичні та астрономічні прилади при вимірюваннях і спостереженнях, до нормалі до поверхні референц-еліпсоїда. Після її введення одержуємо напрям нормального перерізу, утвореного площиною, що проходить через візирну ціль.
-
Поправка за висоту візирної цілі над поверхнею референц-еліпсоїда. Ця поправка забезпечує перехід до прямого нормального перерізу, утвореного площиною, що проходить через проекцію (по нормалі) центра знаку візування на референц-еліпсоїд. Дана редукція зумовлена тим, що нормалі до еліпсоїда у загальному випадку є перехресними прямими, тому проекція пункту, що спостерігається, на референц-еліпсоїд по нормалі не лежить у площині, що включає нормаль до пункту спостереження та виміряний напрям. Після введення вказаних поправок у виміряні горизонтальні напрями отримаємо на поверхні референц-еліпсоїда кут між прямими нормальними перерізами
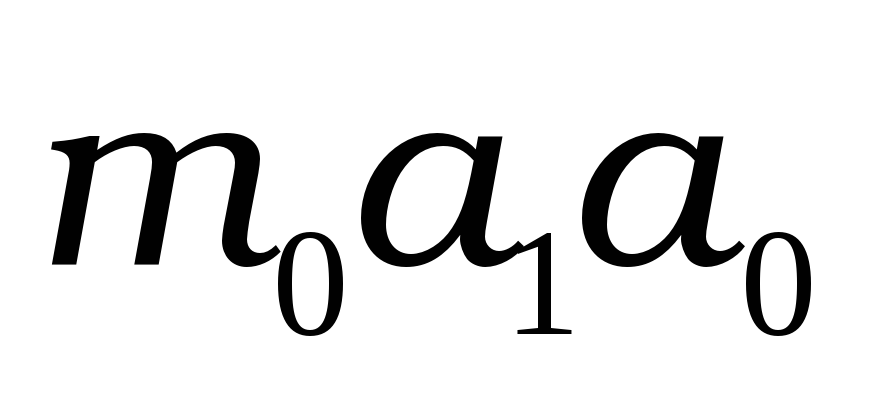та
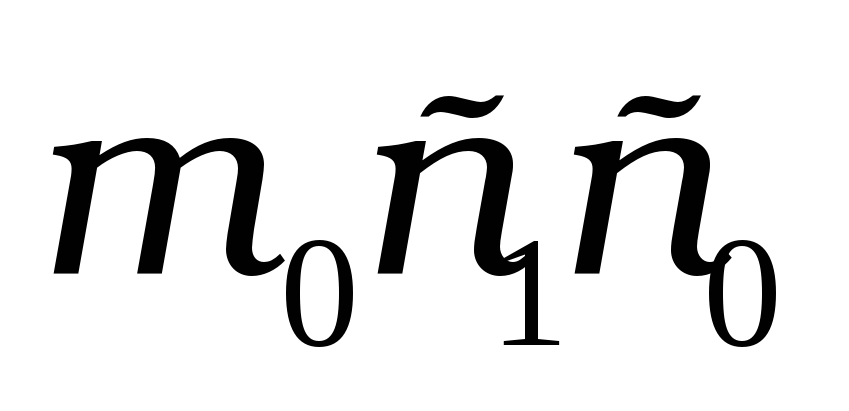з точки
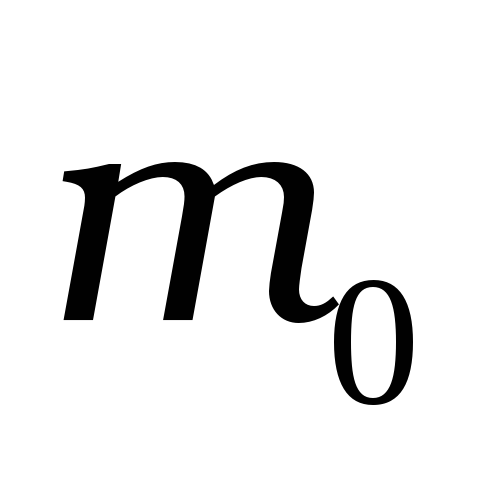на точки
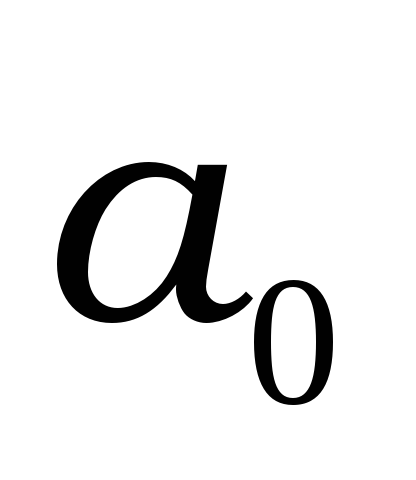і
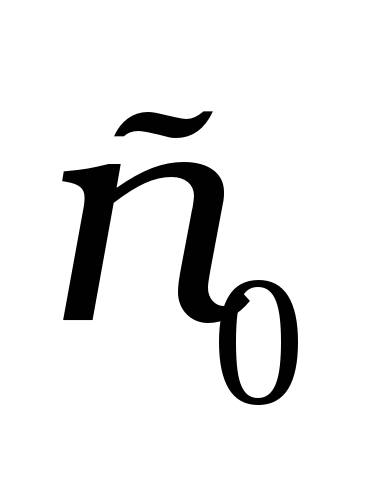(рис.2, б). Оскільки точки на поверхні
еліпсоїда з’єднуються геодезичними
лініями, то необхідно перейти від
напрямів прямих нормальних перерізів
до напрямів геодезичних ліній. -
Поправка за перехід від нормальних перетинів до геодезичних ліній, якими з’єднуються пункти на поверхні референц-еліпсоїда.
-
|
|
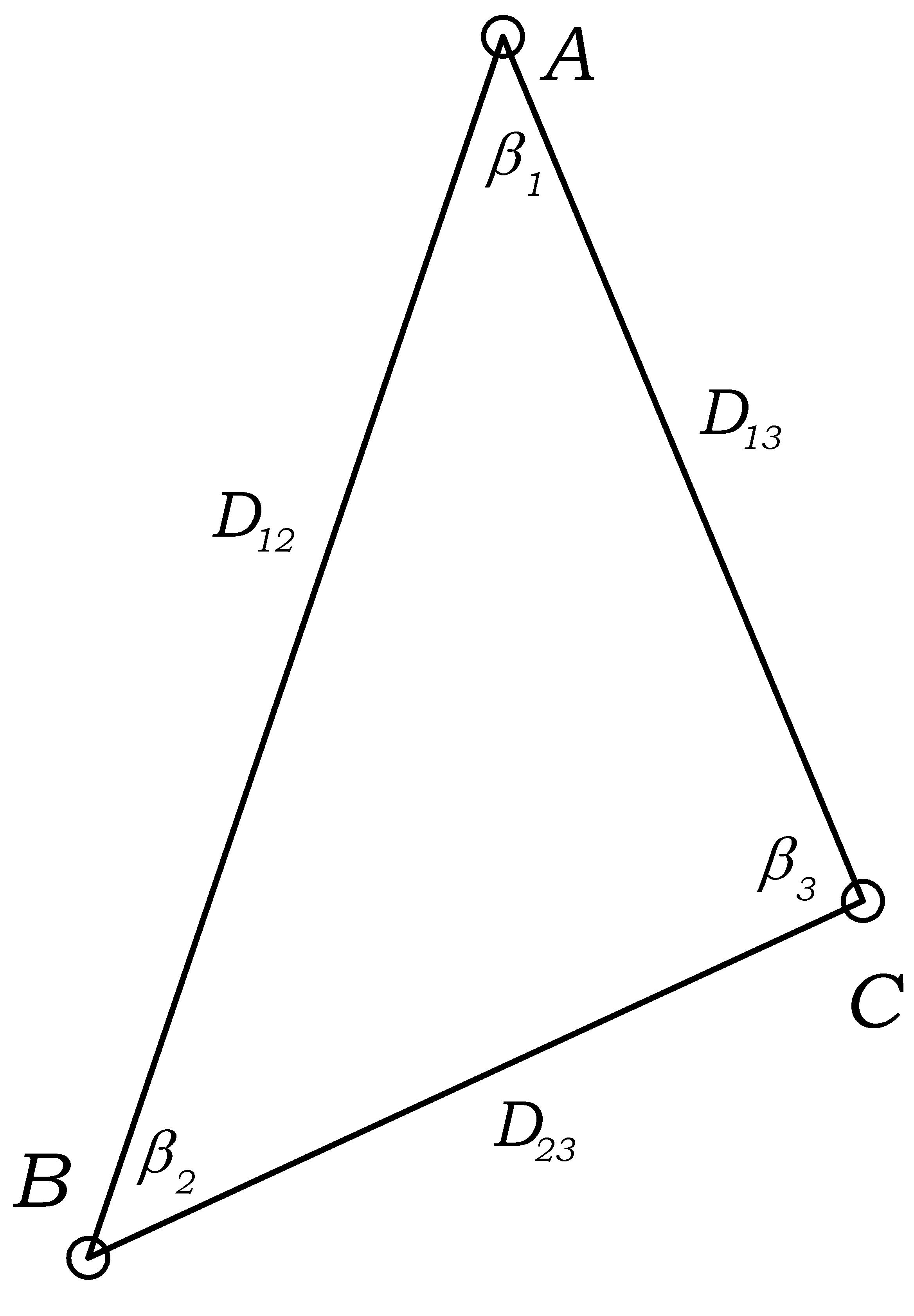
Рис.3. Трикутник тріангуляції 2-го класу, який підлягає редукуванню на еліпсоїд. |
Завдання
1. Спроектувати
виміряну похилу віддаль між пунктами
тріангуляції
і
на поверхню референц-еліпсоїда
Красовського по нормалях.
Вихідні
дані:
геодезичні широта і висота вершин
і
трикутника
тріангуляції 2 класу, довжина виміряної
похилої віддалі
,
геодезичний азимут
.
|
Пункти |
Геодезичні координати |
Геодезичний
азимут,
|
Виміряна
похила віддаль,
|
|
|
|
|
|||
|
|
35°45' |
652,3 |
158°43,6'+30'n |
43 371,25+100n |
|
|
35°29' |
745,9 |
||
,
м
,
м
Послідовність розв’язання задачі
1.
Обчислення поправки за нахил лінії
:
.
2. Обчислення поправки за висоту:
,
де
–
середній радіус
кривини еліпсоїда вздовж даної лінії
,
де
і
–
середні значення висоти і широти даної
лінії.
Довжина
хорди
визначається за формулою:
.
Для контролю довжину хорди обчислюють за формулою:
.
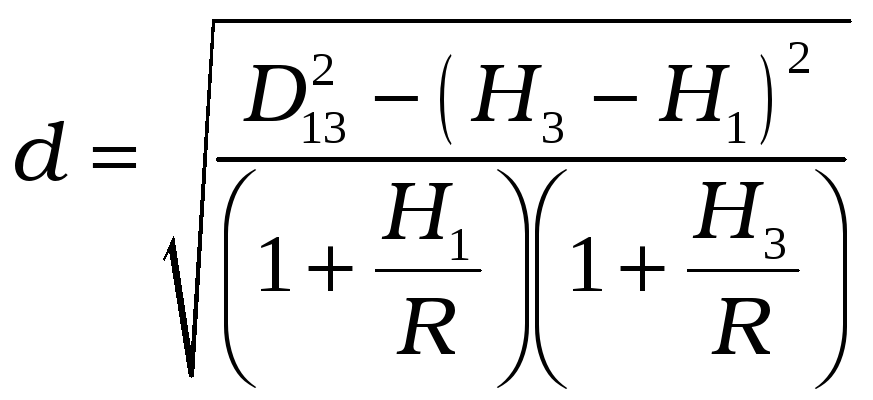Довжину
дуги
обчислюють за формулою:
.
Наведені вище формули можна використовувати для редукування відстаней до сотні кілометрів.
Числовий приклад для нульового варіанту
Вихідні дані:
|
№ пунктів |
Геодезичні координати |
Геодезичний
азимут,
|
Виміряна
похила віддаль,
|
|
|
|
|
|||
|
1 |
35°45' |
652,3 |
158°43,6' |
43 371,252 |
|
3 |
35°29' |
745,9 |
||
,
м
,
м
Розв’язання задачі
|
|
-0,1010 |
|
|
699,1 |
|
|
35°37' |
|
|
6 360 984,8020 |
|
|
-4,7662 |
|
|
43 366,3828 |
|
|
43 366,3828 |
|
|
43 366,467 |
,
м
,
м
,
м
,
м
,
м
,
м, контрольне
,
мЗавдання 2. Редукувати виміряні на земній поверхні кути трикутника тріангуляції 2 класу на референц-еліпсоїд Красовського.
Вихідні
дані:
геодезичні широта і висота вершин
і
трикутника
тріангуляції 2 класу, значення складових
астрономо-геодезичних відхилень
прямовисних ліній
і
у точці встановлення приладу, довжини
сторін трикутника
,
геодезичні азимути
та виміряні астрономічні зенітні віддалі
спостережуваних напрямків.
|
Номер пункту |
Геодезичні координати |
Складові відхилень прямовисних ліній |
||
|
|
|
|
|
|
|
|
35°45' |
652,3 |
+5,34" |
-0,25" |
|
|
35°25' |
845,4 |
-5,41" |
+12,15" |
|
|
35°29' |
745,9 |
-15,36" |
+5,91" |
,
м
|
Пункт |
Номер напрямку |
|
|
|
Виміряні кути, |
|
|
|
38,91 |
200°05,8' |
89°53,5' |
41°23'02,1"-30'n |
|
|
43,37+0,1n |
158°43,6'+30'n |
90°04,4' |
||
|
|
|
44,50 |
66°37,5' |
90°19,6' |
46°30'23,8" |
|
|
38,91 |
20°05,8' |
90°27,5' |
||
|
|
|
43,37+0,1n |
338°43,6'+30'n |
89°18,8' |
92°06'39,7"+30'n |
|
|
44,50 |
246°37,5' |
90°04,3' |
,
км
Послідовність розв’язання задачі
1.
Обчислення поправки
за відхилення прямовисної лінії від
нормалі для напрямку
за формулою:
.
2.
Обчислення поправки
за висоту візирної цілі
,
яка спостерігається з пункту
,
над поверхнею референц-еліпсоїда за
формулою:
,
де
–
радіус кривини меридіана на широті
.
3.
Обчислення поправки
для пункту спостереження за перехід
від нормальних перетинів до геодезичних
ліній за формулою:
,
де
–
радіус кривини першого вертикалу на
широті
.
Ця формула використовується при
км
і
.
Всі поправки обчислюють для кожного напрямку з точністю до 0,001".
Обчислення суми поправок для кожного напрямку:
.
4. Обчислення поправок у кожний кут:
,
обчислення значень редукованих на поверхню референц-еліпсоїда кутів:
.
5. Обчислення сферичного надлишку за значеннями редукованих кутів та нев’язки трикутника. Сферичний надлишок обчислюється за формулою:
,
де
–
середній радіус кривини еліпсоїда,
обчислений на середній широті лінії
.
Нев’язка трикутника обчислюється за формулою:
.
Числовий приклад для нульового варіанту
Вихідні дані:
|
Пункти |
Геодезичні координати |
Складові відхилень прямовисних ліній |
||
|
|
|
|
|
|
|
|
35°45' |
652,3 |
+5,34" |
-0,25" |
|
|
35°25' |
845,4 |
-5,41" |
+12,15" |
|
|
35°29' |
745,9 |
-15,36" |
+5,91" |
,
м
|
Пункти |
Номер напрямку |
|
|
|
Виміряні кути, |
|
|
|
38,91 |
200°05,8' |
89°53,5' |
41°23'02,1" |
|
|
43,37 |
158°43,6' |
90°04,4' |
||
|
|
|
44,50 |
66°37,5' |
90°19,6' |
46°30'23,8" |
|
|
38,91 |
20°05,8' |
90°27,5' |
||
|
|
|
43,37 |
338°43,6' |
89°18,8' |
92°06'39,7" |
|
|
44,50 |
246°37,5' |
90°04,3' |
,
км
Розв’язання задачі
1. Обчислення поправки за відхилення прямовисних ліній.
|
Пункти |
Відхилення виска, і |
Спостережуваний напрямок |
|
|
|
|
|
+5,34" |
|
200°05,8' |
89°53,5' |
+0,004" |
|
-0,25" |
|
158°43,6' |
90°04,4' |
+0,002" |
|
|
|
-5,41" |
|
66°37,5' |
90°19,6' |
-0,056" |
|
+12,15" |
|
20°05,8' |
90°27,5' |
-0,106" |
|
|
|
-15,36" |
|
338°43,6' |
89°18,8' |
-0,001" |
|
+5,91" |
|
246°37,5' |
90°04,3' |
+0,021" |
