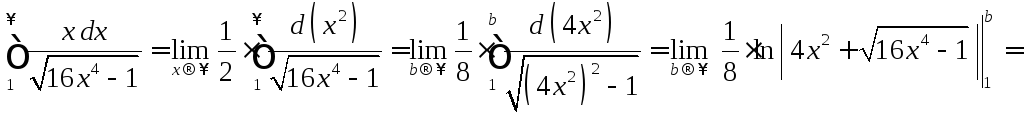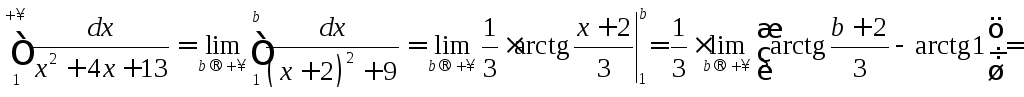- •Математический анализ (Часть I)
- •Оглавление введение Правила оформления контрольной работы
- •Порядок выполнения контрольной работы для всех специальностей и форм обучения
- •Задания контрольной работы
- •Пределы
- •Исследование функции на непрерывность
- •Определённый интеграл
- •Задания с экономическим содержанием
- •Образцы решения заданий контрольной работы
- •Приложение
Задания с экономическим содержанием
Указание: вместоnподставить номер вашего варианта.
Задание
48. Функции
спроса и предложения на некоторый товар
на рынке описываются зависимостями
вида:![]() .
.
Найти:
наибольшую равновесную цену
 ;
;пределы отношений спроса и предложения, характеризующие различные изменения ситуации на рынке:
![]() ;
;
эластичность спроса на товар в точке равновесной цены
 .
.
Задание
49. Пусть
![]() количество реализованного товара, при
этом функции
затрат и дохода описываются
зависимостями вида:
количество реализованного товара, при
этом функции
затрат и дохода описываются
зависимостями вида:
![]() .
.
Определить:
средние и предельные издержки при
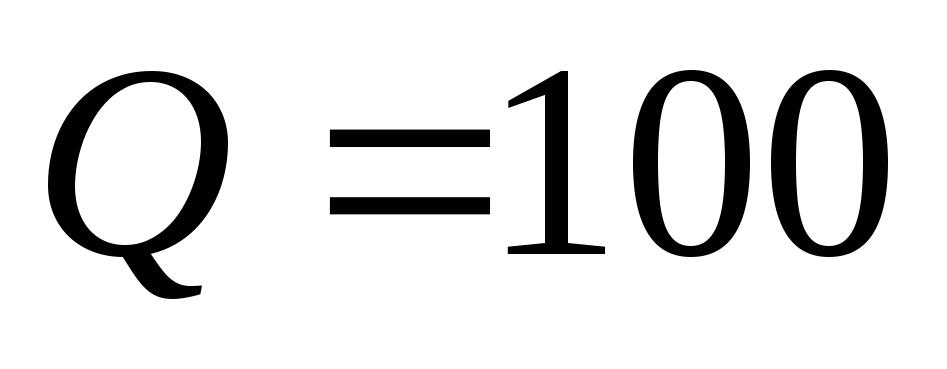 ;
;найти максимум прибыли:
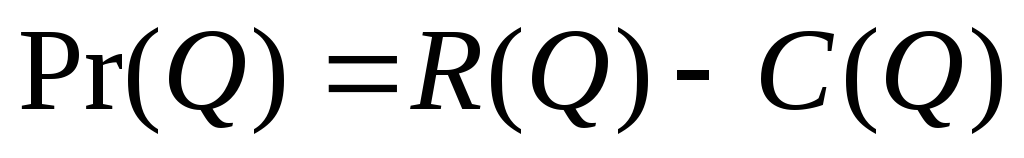 .
.
Образцы решения заданий контрольной работы
Задание
1. Доказать,что ![]() ,указать
,указать
![]() .
.
Доказательство:
Согласно
определению предела числовой
последовательности необходимо для
любого
![]() найти номер
найти номер![]() такой, что при любых
такой, что при любых![]() выполнялось неравенство
выполнялось неравенство![]() .
.
Рассмотрим
модель
![]() .
.
Так
как
![]() можно записать цепочку неравенств
можно записать цепочку неравенств![]() .
.
То
есть, поскольку нам не требуется найти
наименьшее
![]() ,
можно записать
,
можно записать![]() ,
откуда
,
откуда![]() и в этом случае
и в этом случае![]() —
целая часть числа
—
целая часть числа![]() .
.
Итак,
получается, что при
![]() выполнено неравенство
выполнено неравенство![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Задание
2. Вычислить
предел числовой последовательности 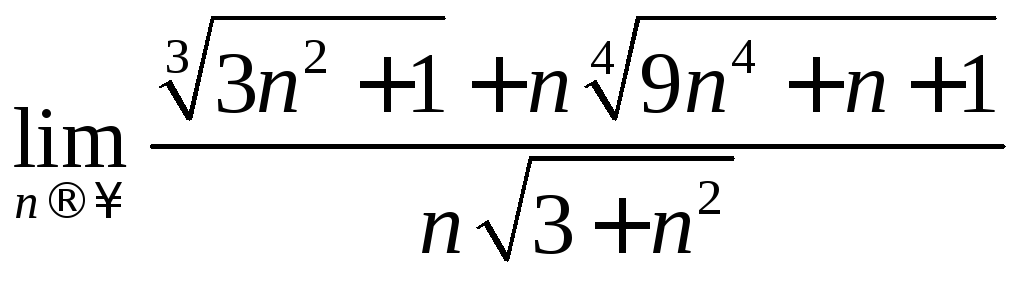 .
.
Решение:
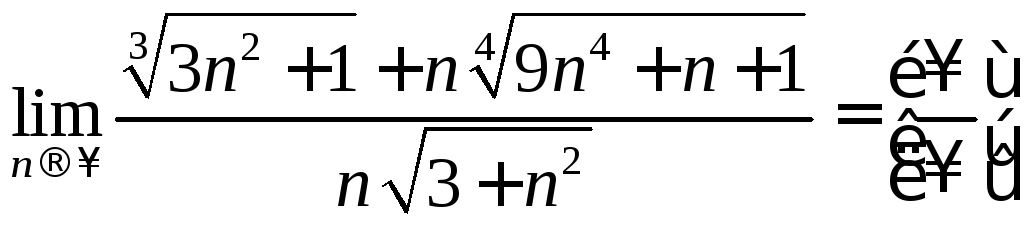 .
.
Для
раскрытия неопределённости данного
вида преобразуем выражения, стоящие
под знаками пределов, поделив и числитель,
и знаменатель на наибольшую степень![]() .
Для этогосначала определим наибольшую
степень числителя, а затем знаменателя.
.
Для этогосначала определим наибольшую
степень числителя, а затем знаменателя.
Для
числителя имеем:
![]() ~
~![]() и
и![]() ~
~![]() ,
следовательно, получим
,
следовательно, получим![]() ,
а для знаменателя —
,
а для знаменателя —![]() ~
~![]() ,
т. е. тоже
,
т. е. тоже![]() .
.
Поделим
и числитель, и знаменательна
![]() :
:
![]()
![]()
![]() .
.
Следовательно, 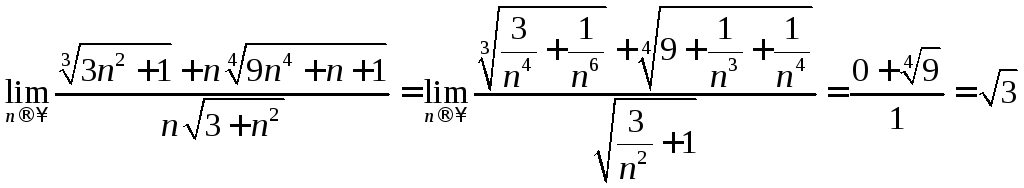 .
.
Задание
3. Вычислить
предел числовой последовательности ![]() .
.
Решение:
Заметим,
что![]() ,
а
,
а![]() ,
поэтому
,
поэтому![]()
Неопределенностьвида![]() раскрывается с помощью второго
замечательного предела
раскрывается с помощью второго
замечательного предела![]() .
.
Преобразуем выражение, стоящее под знаком предела следующим образом:
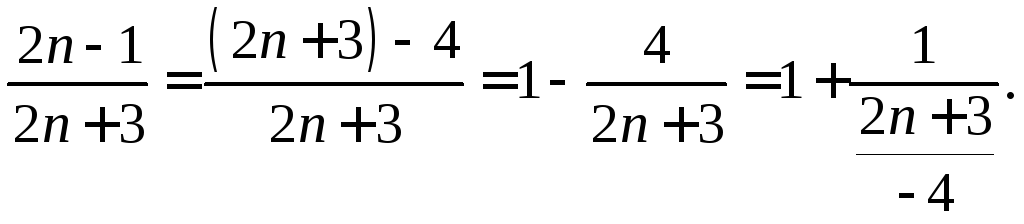
Итак, 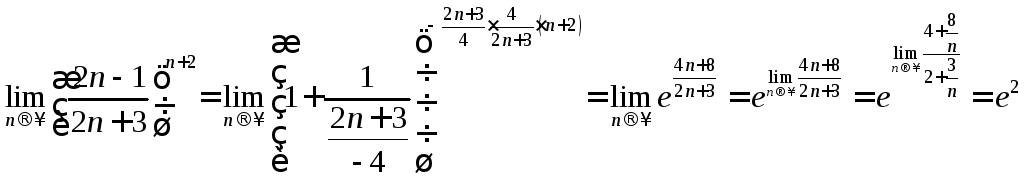 .
.
Задание
4. Вычислить
предел функции ![]() .
.
Решение:
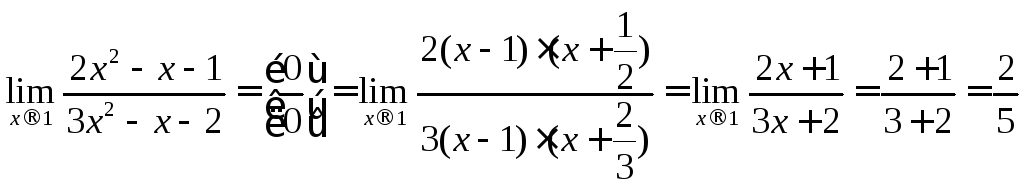 .
.
Задание
5. Вычислить
предел: ![]() .
.
Решение:
![]()
Для
раскрытия неопределенности
![]() разложим числитель и знаменатель дроби,
стоящей под знаком предела, на множители.
Заметим, что
разложим числитель и знаменатель дроби,
стоящей под знаком предела, на множители.
Заметим, что![]() .
Так как при
.
Так как при![]()
![]() ,
значит,
,
значит,![]() делится на
делится на![]() .
.
Поделим«столбиком»
многочлен ![]() на
двучлен
на
двучлен![]() :
:
|
_
|
|
|
|
|
|
|
|
| ||
|
_
|
|
|
|
|
|
|
|
_
|
|
|
|
|
|
|
|
0 |
|
|
Следовательно, 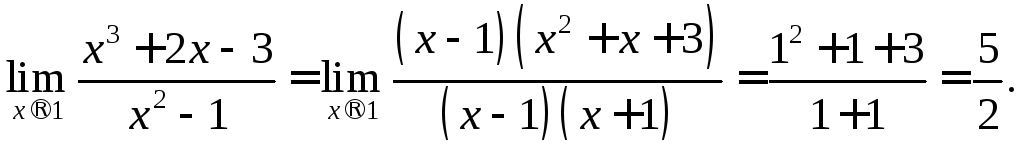
Задание
6. Вычислить
предел функции ![]() .
.
Решение:
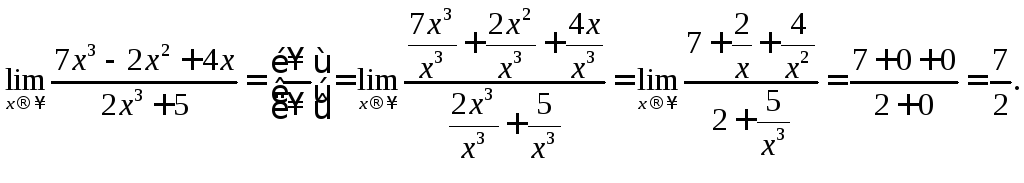
Задание
7. Вычислить
предел функции ![]()
Решение:
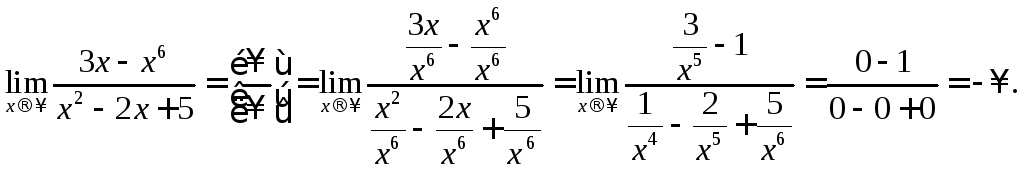
Задание
8. Вычислить
предел функции ![]() .
.
Решение:
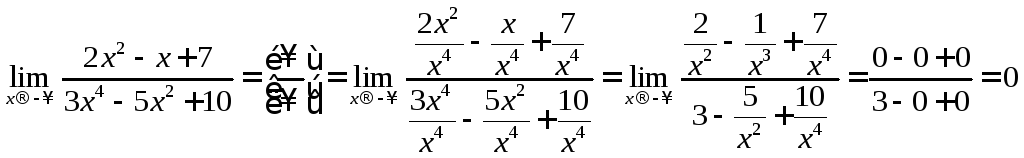 .
.
Задание
9. Вычислить
предел функции ![]() .
.
Решение:
![]() .
.
Раскроем эту неопределенность, умножив числитель и знаменатель дроби на выражение,сопряженное числителю и преобразуем результат:
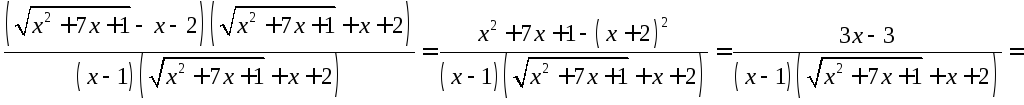
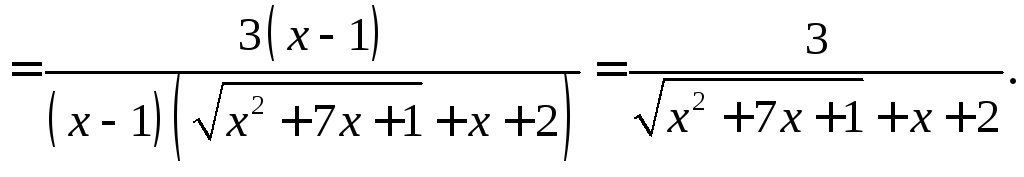
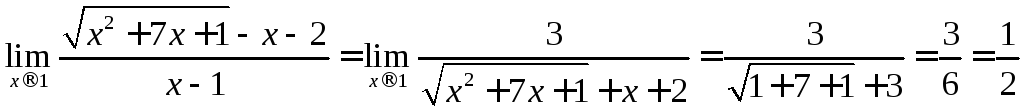 .
.
Задание
10. Вычислить
предел функции ![]() .
.
Решение:
Заметим,
что![]() ,
а
,
а![]() ,
поэтому
,
поэтому![]()
Неопределенностьвида![]() раскрывается с помощью второго
замечательного предела
раскрывается с помощью второго
замечательного предела![]() .
.
Преобразуем выражение, стоящее под знаком предела следующим образом:
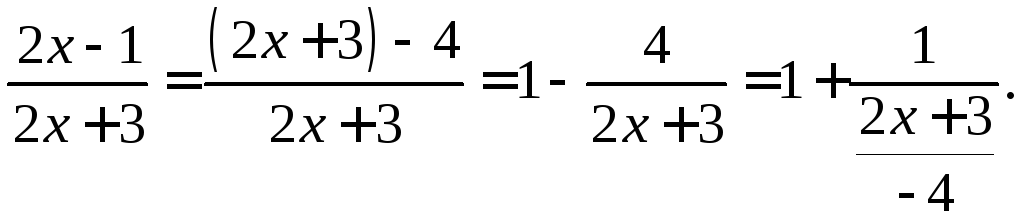
Итак, 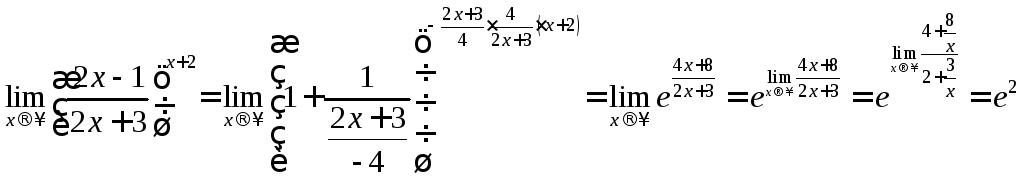 .
.
Задание
11. Вычислить
предел функции ![]() .
.
Решение:
Заметим,
что
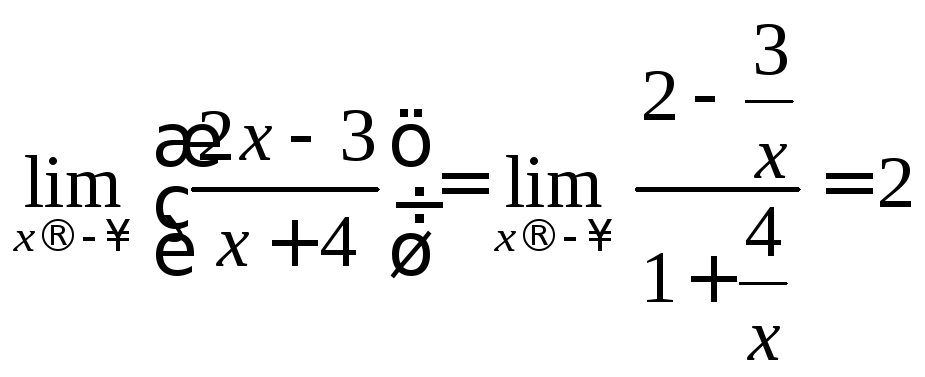 ,
а
,
а![]() ,
поэтому искомый
предел равен
,
поэтому искомый
предел равен![]() ,
т. е.
,
т. е.![]() .
.
Задание
12. Вычислить
предел функции ![]() .
.
Решение:
Воспользуемся
первым замечательным пределом
![]() .
.
Имеем: ![]()
![]()
![]() .
.
Задание
13. Исследовать
функцию 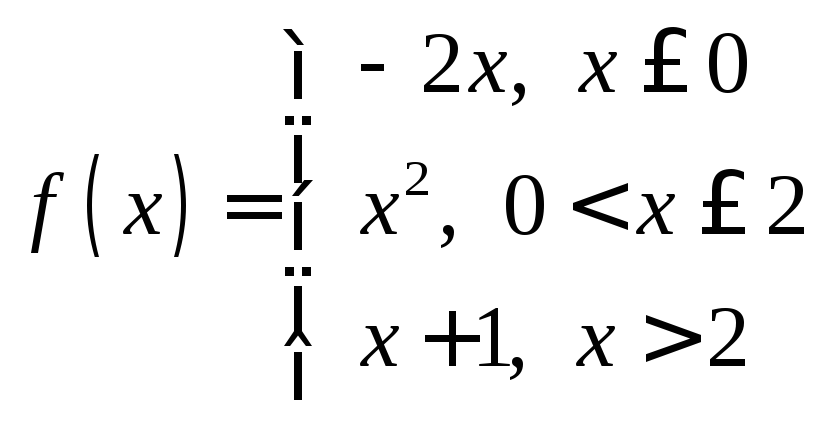 на
непрерывность.
на
непрерывность.
Решение:
Поскольку
элементарные функции непрерывны, то
данная функция
![]() непрерывна
всюду за исключением, быть может, двух
точек:
непрерывна
всюду за исключением, быть может, двух
точек:![]() и
и![]() .
.
Исследуем
функцию
![]() на непрерывность в этих точках.
на непрерывность в этих точках.
Для
этого найдем пределы функции в
точках ![]() и
и ![]() слева
и справа:
слева
и справа:
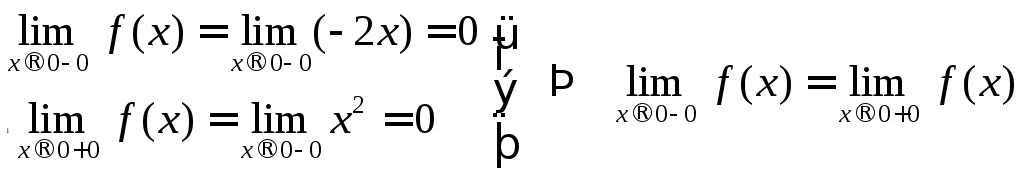 ,значит
,значит ![]() .
.
Найдем
![]() .
.
![]() ,
т. е.
,
т. е.![]() ,
следовательно, функция непрерывна в
точке
,
следовательно, функция непрерывна в
точке![]() .
.
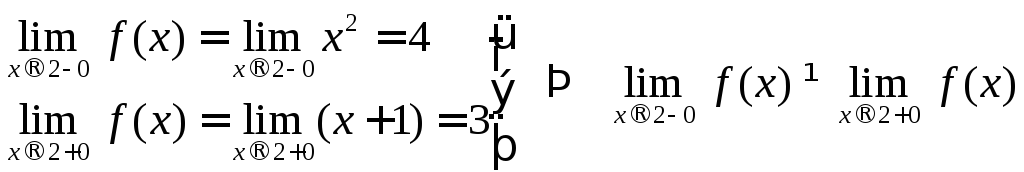 ,следовательно,
в точке
,следовательно,
в точке
![]() функция терпит разрыв.
функция терпит разрыв.
Таким
образом, исходная функция
![]() непрерывна
всюду кроме точки
непрерывна
всюду кроме точки![]() ,
которая является точкой разрыва первого
рода.
,
которая является точкой разрыва первого
рода.
Задание
14. Исследовать
на непрерывность функцию
![]() в точках
в точках![]() и
и![]() .
.
Решение:
Легко
видеть, что при ![]()
![]() ,
таким образом, в точке
,
таким образом, в точке![]() данная
функция непрерывна, а в точке
данная
функция непрерывна, а в точке![]() функция
функция![]() неопределенна.
неопределенна.
Найдем левый и правый пределы функции в этой точке:
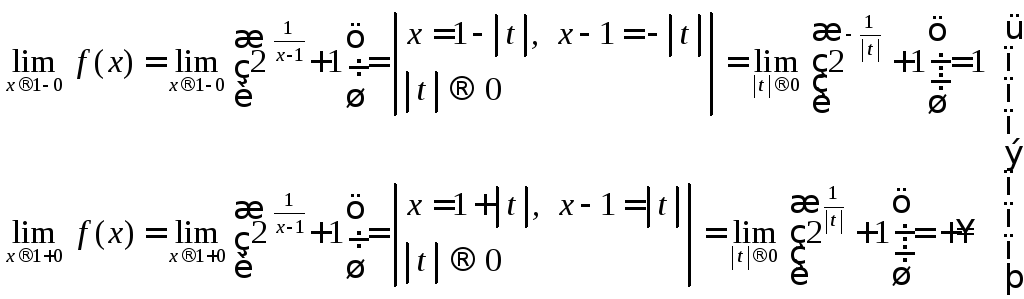
![]()
![]() значит, точка
значит, точка![]() является
точкой разрыва функции,
а поскольку
один из пределов бесконечен, то эта
точка разрыва второго рода.
является
точкой разрыва функции,
а поскольку
один из пределов бесконечен, то эта
точка разрыва второго рода.
Задание
15.1 Найти
производную функции ![]() .
.
Решение:
![]() .
.
Задание
16. Найти
производную функции ![]() .
.
Решение:
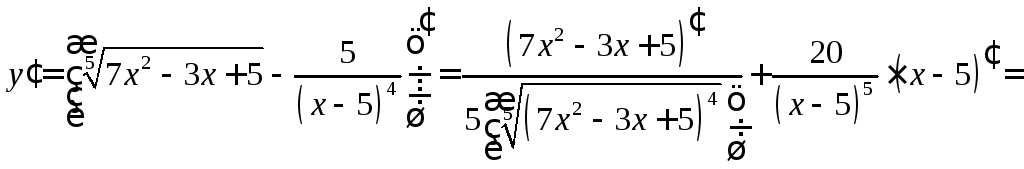
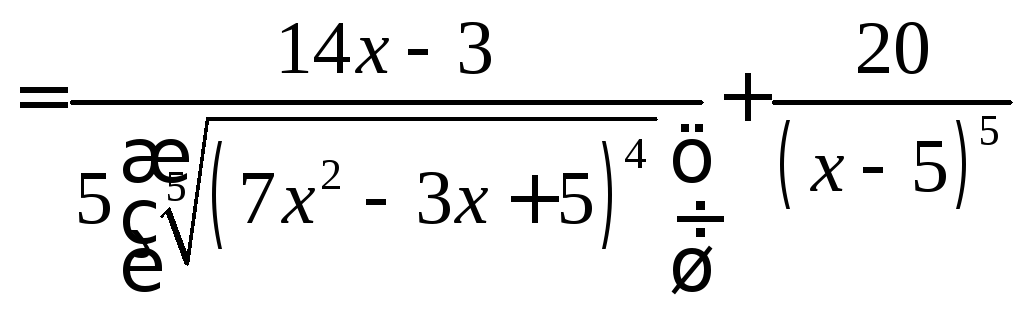 .
.
Задание
17. Найти
производную функции ![]() .
.
Решение:
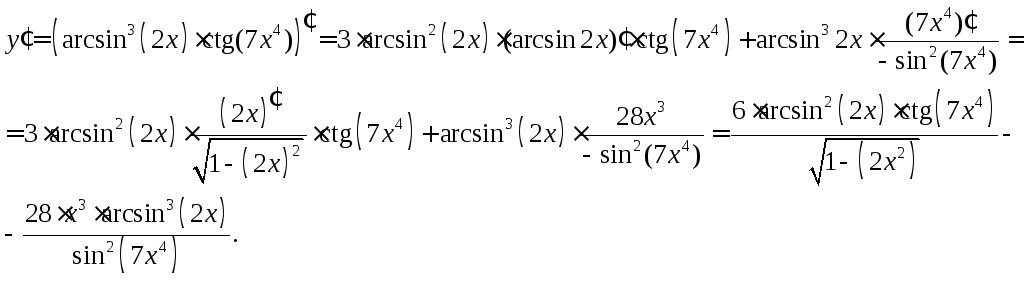
Задание
18. Найти
производную функции 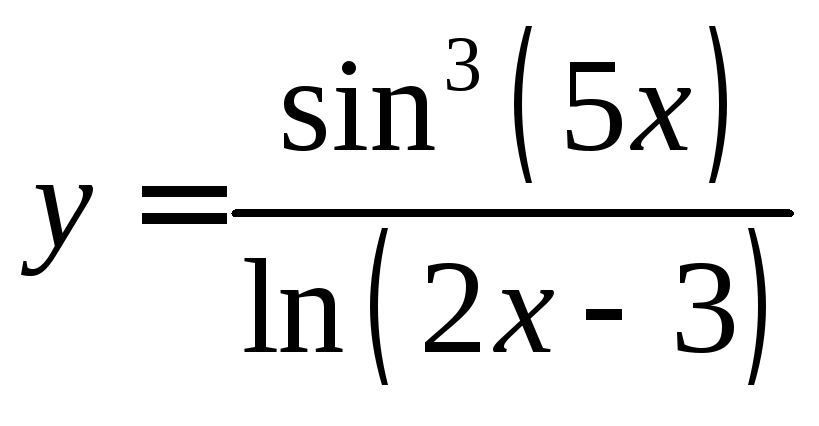 .
.
Решение:
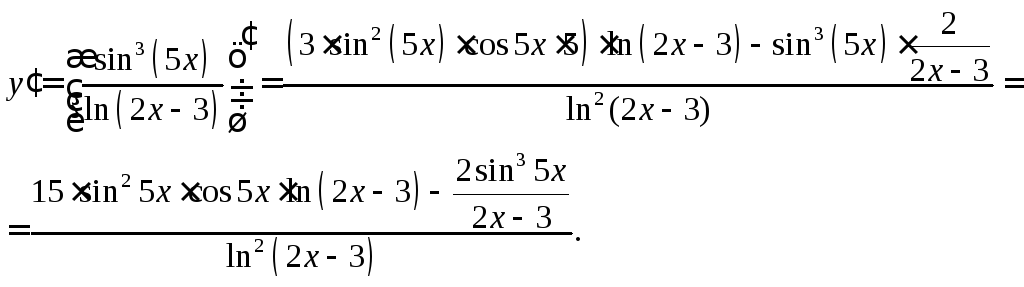
Задание
19. Для
функции ![]() и
и![]() вычислить
вычислить
![]() .
.
Решение:
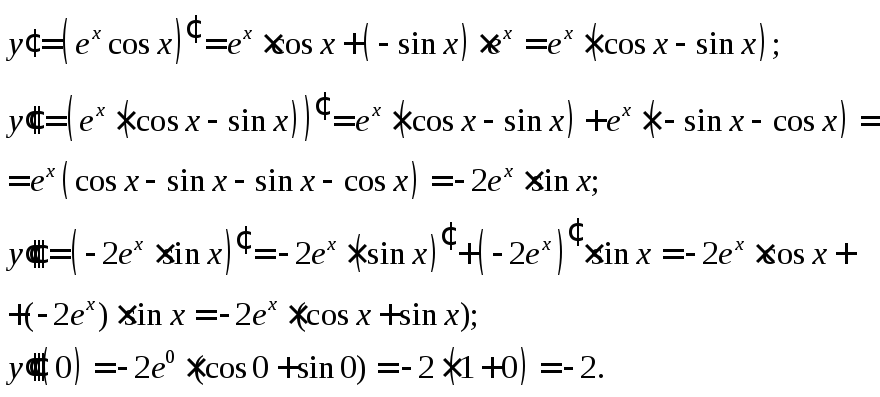
Задание
20. Найти
производную n-го
порядка функции ![]() .
.
Решение:
![]() ;
;
![]() ;
;
![]() ;
и т. д.
;
и т. д.
Исходя
из полученного, можно выявить следующую
закономерность: ![]() .
.
Задание
21.2 Вычислить
предел 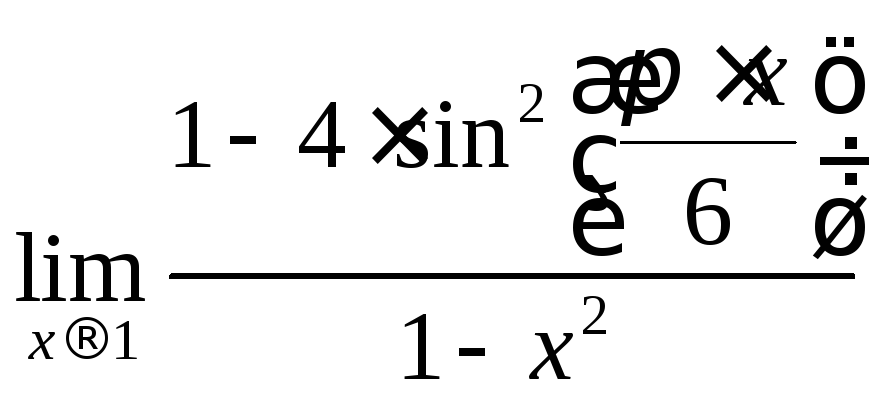 .
.
Решение:
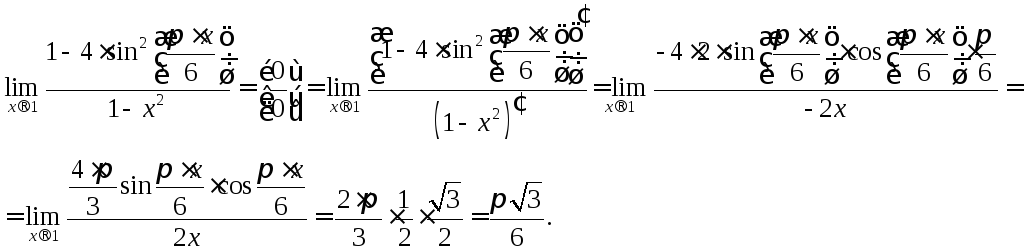
Задание
22. Вычислить
предел 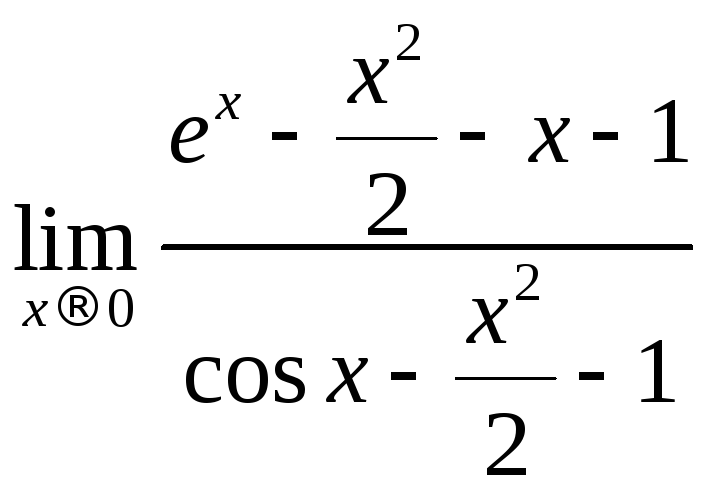 .
.
Решение:
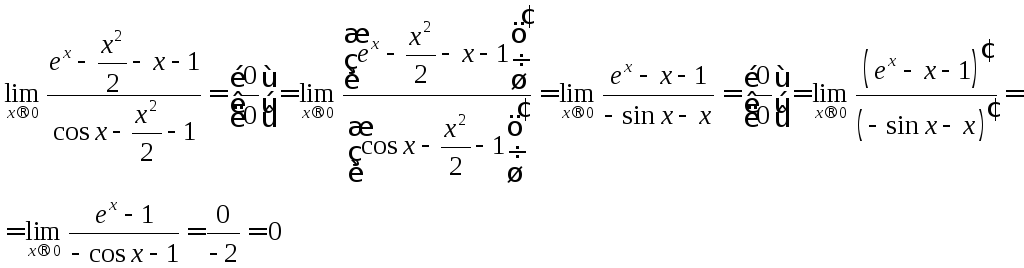
Задание
23. Вычислить
предел ![]() .
.
Решение:
![]() ,
т. е. сразу правило Лопиталя применить
нельзя.
,
т. е. сразу правило Лопиталя применить
нельзя.
Путём
тождественных преобразований выражения,
стоящего под знаком предела, сначала
сведём неопределённость вида![]() к неопределённости вида
к неопределённости вида![]() :
:

Задание
24. Вычислить
предел ![]() .
.
Решение:
![]()
Задание
25. Провести
полное исследование функции
![]() и построить её график.
и построить её график.
Решение:
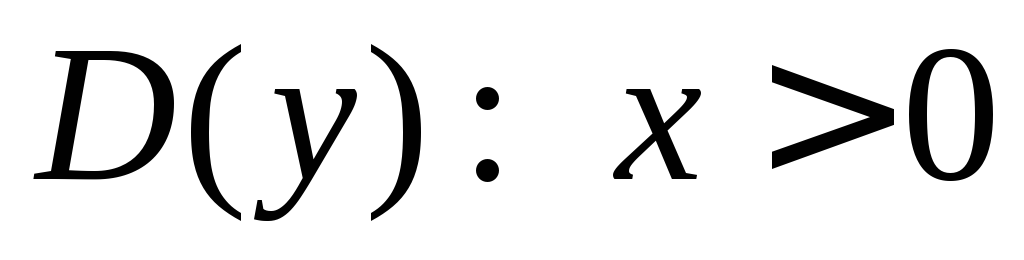 .
.Так как область определения не симметрична относительно нуля, то функция
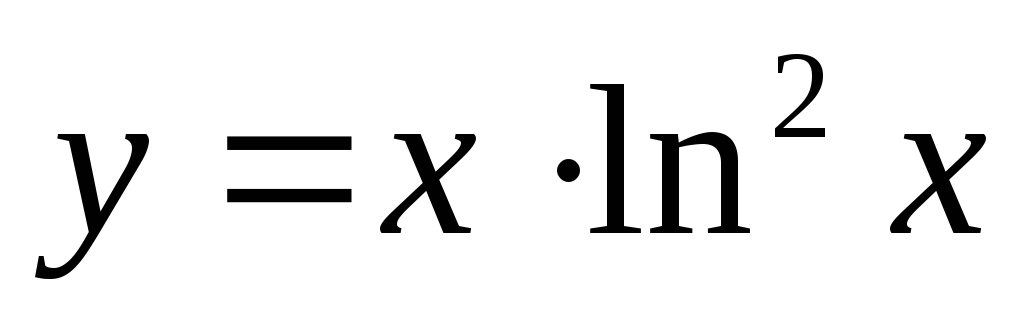 является
функцией общего вида.
является
функцией общего вида.Нули функции:
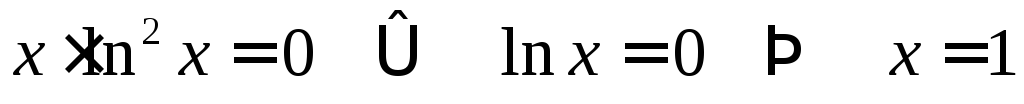 .
.Пересечений с осью ординат нет, так как
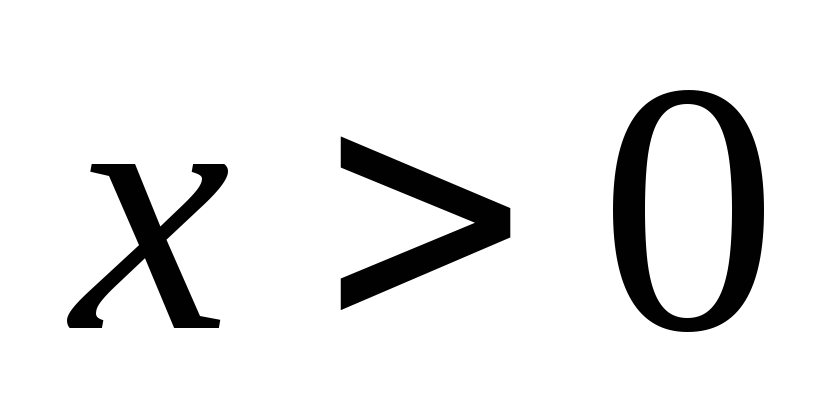 .
.Найдём асимптоты:
Вертикальная асимптота:
 .
Исследуем поведение функции вблизи
асимптоты справа. Для этого найдем
предел:
.
Исследуем поведение функции вблизи
асимптоты справа. Для этого найдем
предел:
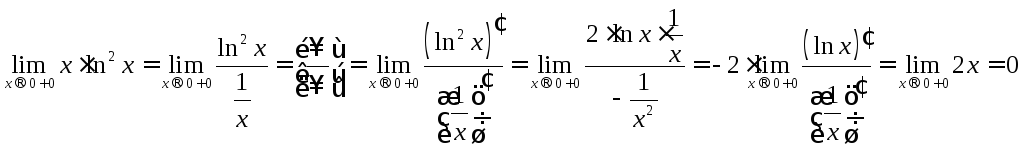 .
.
Наклонные асимптоты:
![]() ,
т. е. наклонных асимптот нет.
,
т. е. наклонных асимптот нет.
Горизонтальных асимптот нет.
Найдем экстремумы функции:
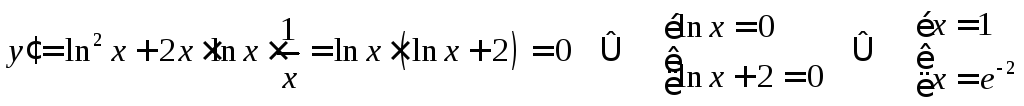 .
.
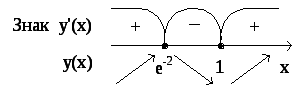
Рис. 1.
Из
рис.1 следует, что
![]() — точка максимума, а
— точка максимума, а
![]() — точка минимума.
— точка минимума.
![]() ,
, ![]() .
.
Найдем точки перегиба:
![]() .
См. рис. 2.
.
См. рис. 2.

Рис. 2.
![]() —ордината
точки перегиба.
—ордината
точки перегиба.
Сведём в таблицу все результаты проведённого исследования.
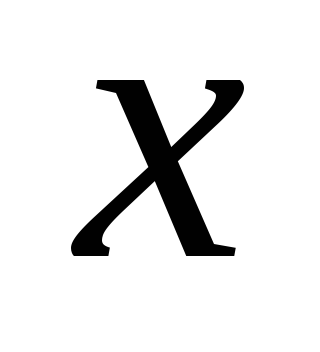
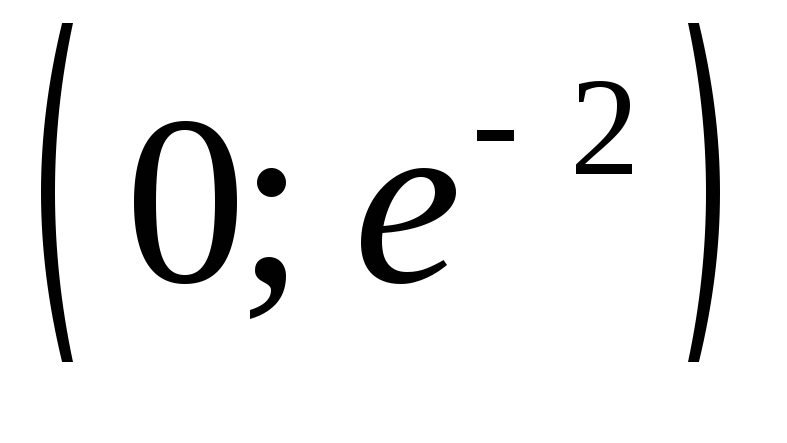
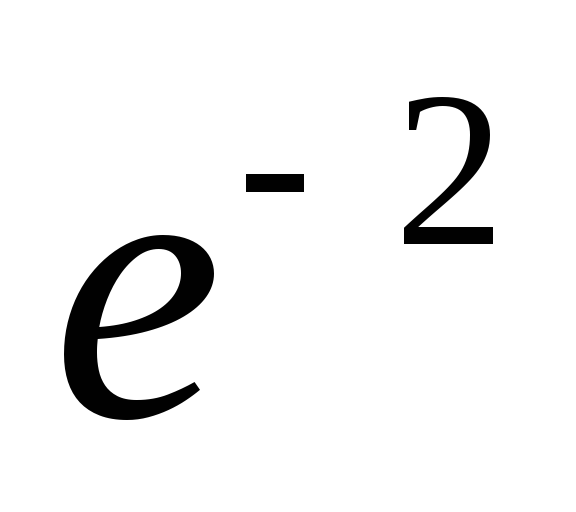
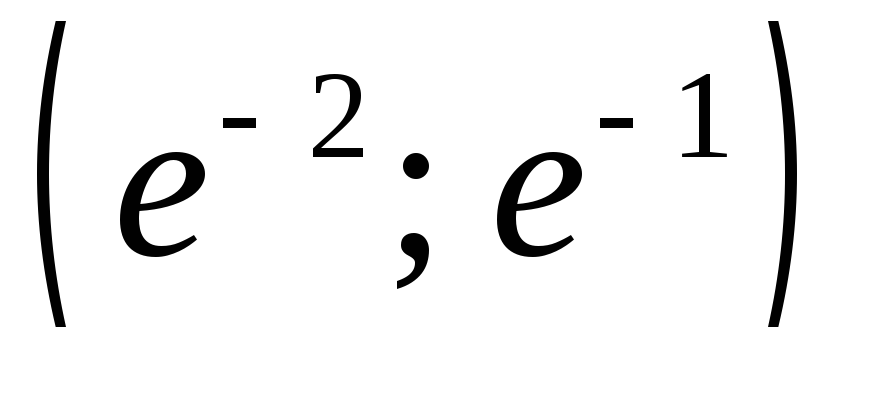
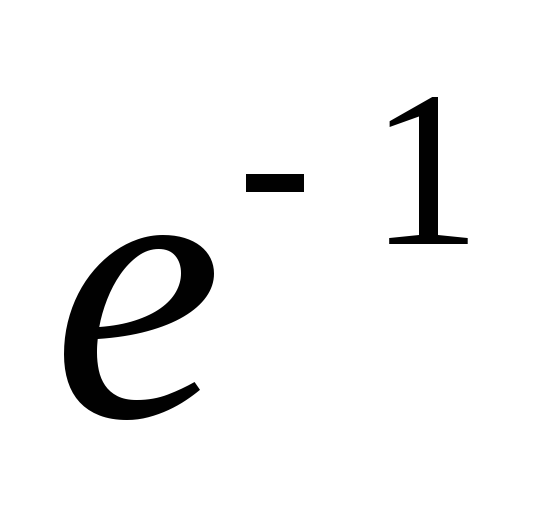
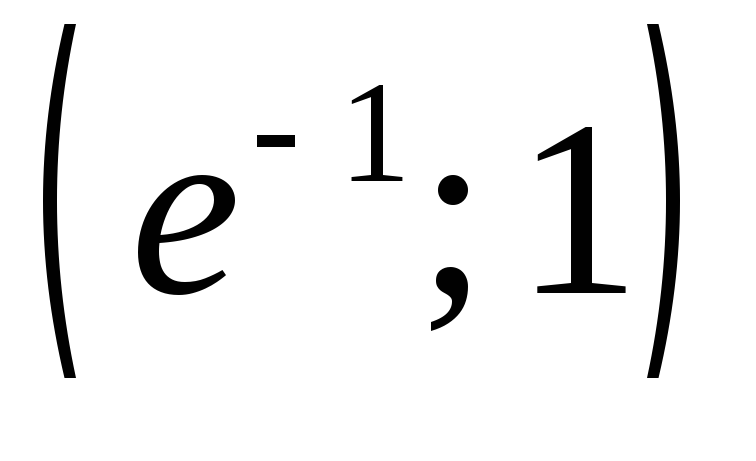
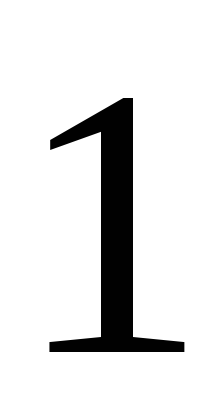
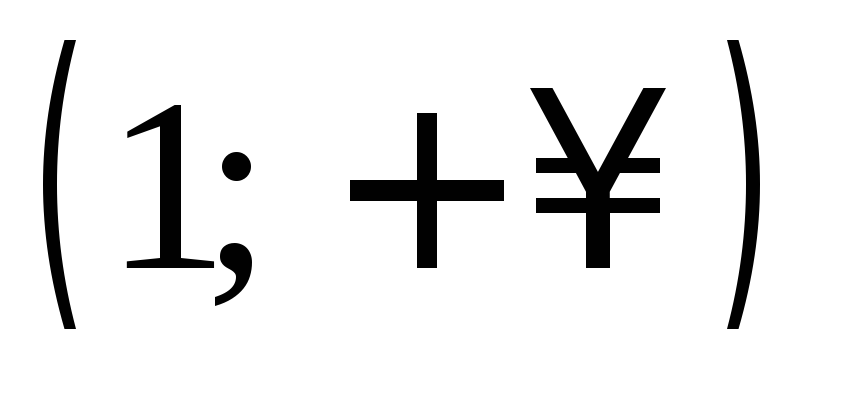
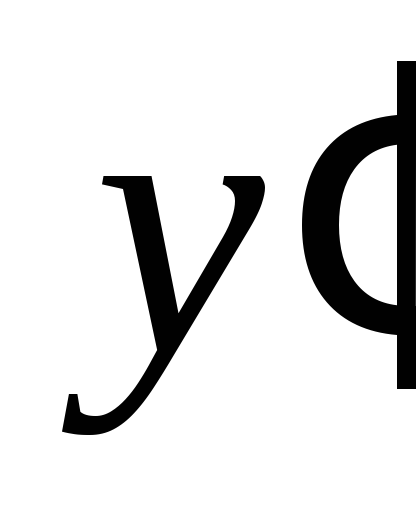


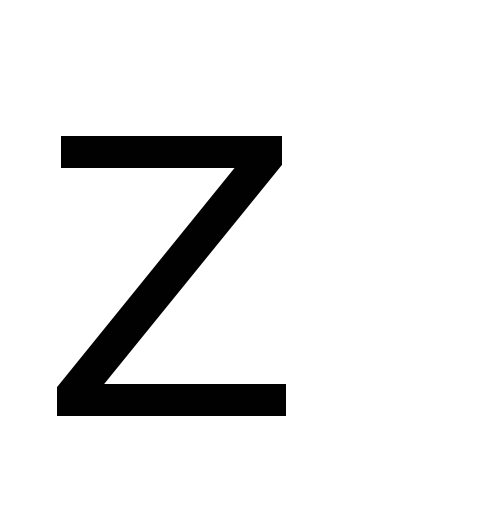
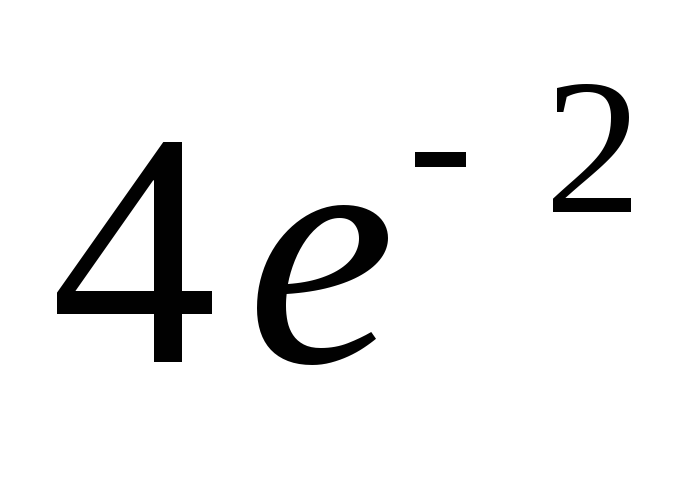
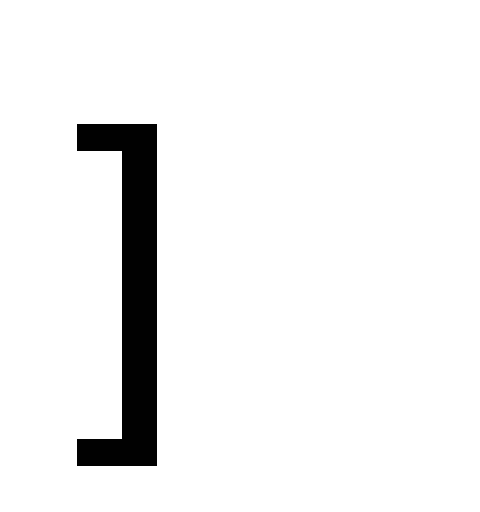
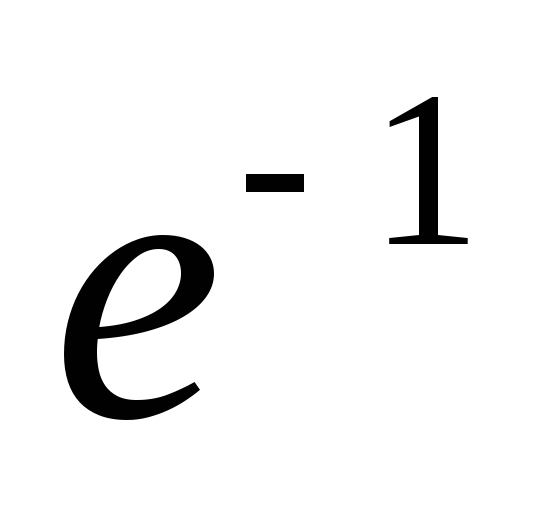


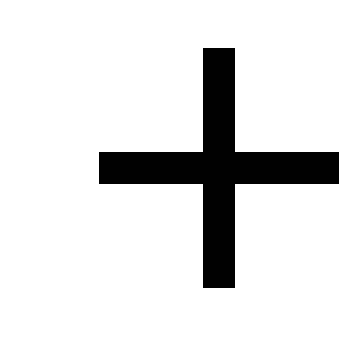

Точка перегиба


График данной функции представлен на рис. 5.
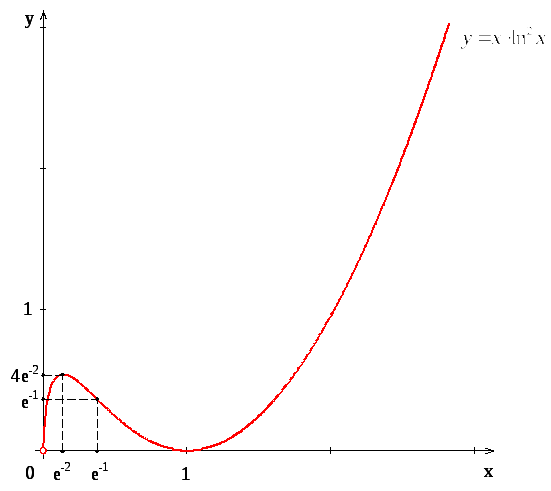
Рис. 5.
Задание
26. Провести
полное исследование функции 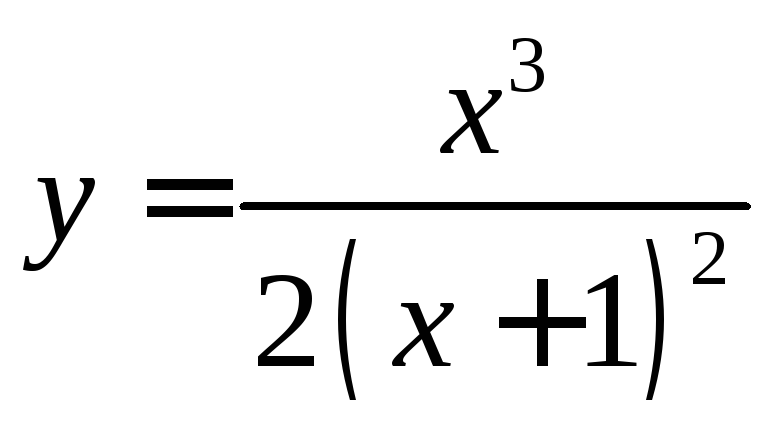 и построить её график.
и построить её график.
Решение:
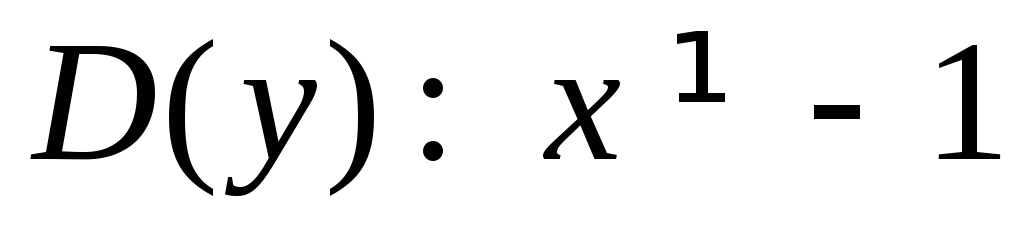 .
В точке
.
В точке
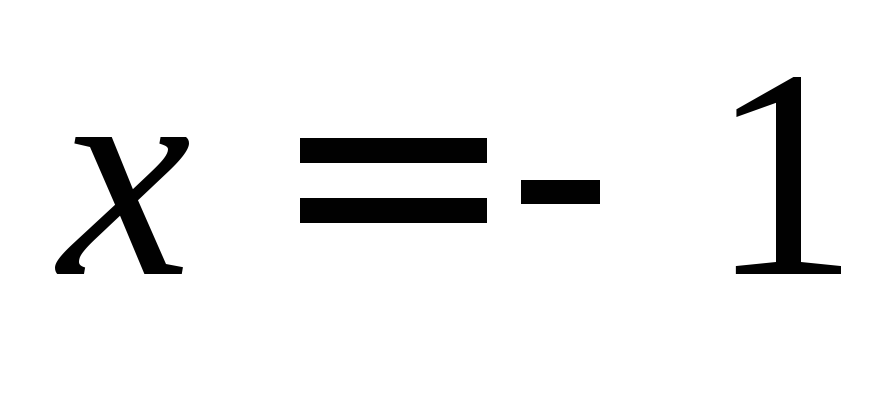 знаменатель данной функции обращается
в ноль, следовательно функция в ней не
определена — терпит разрыв.
знаменатель данной функции обращается
в ноль, следовательно функция в ней не
определена — терпит разрыв.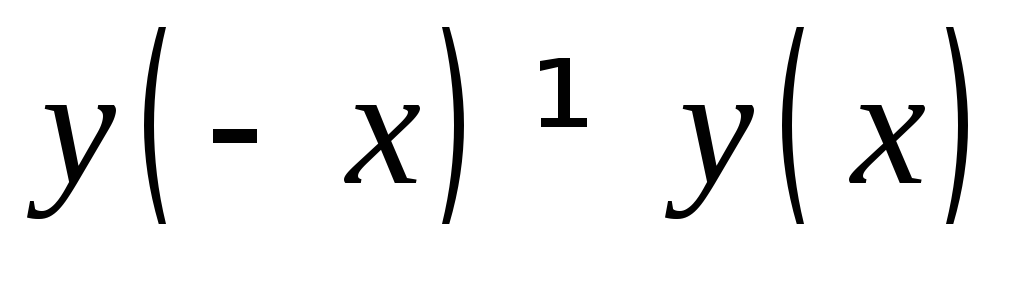 и
и
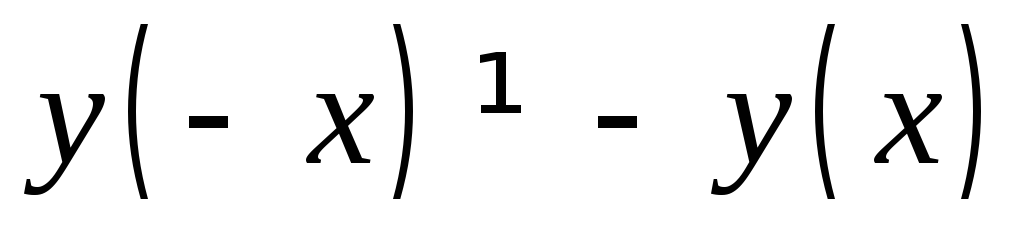 ,
следовательно функция общего вида.
,
следовательно функция общего вида.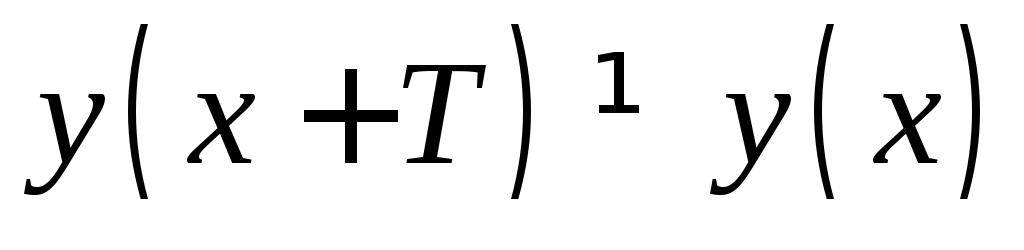 ,
следовательно функция непериодическая.
,
следовательно функция непериодическая.Нули функции:
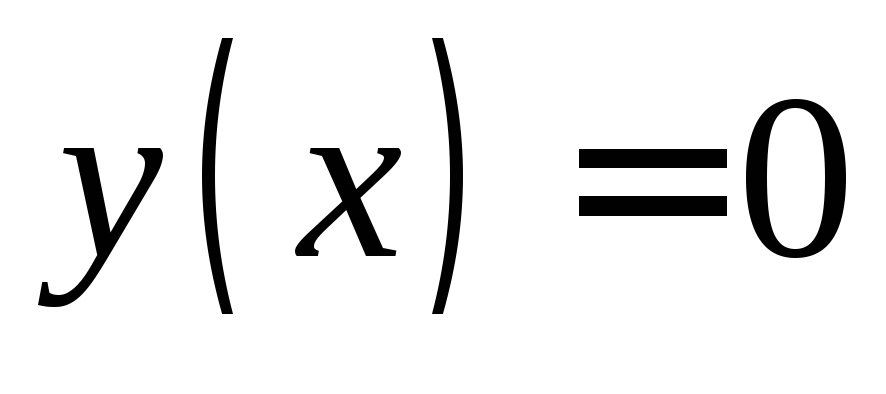 при
при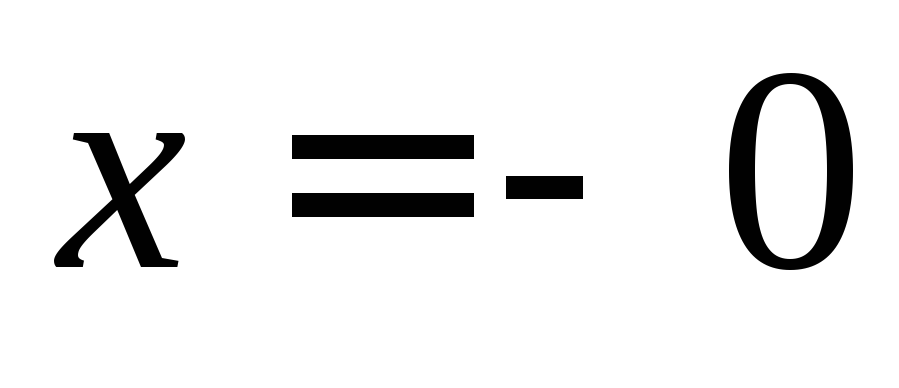 .
.Найдем асимптоты данной функции:
Вертикальная асимптота:
 и
и ,
отсюда следует, что существует
вертикальная асимптота
,
отсюда следует, что существует
вертикальная асимптота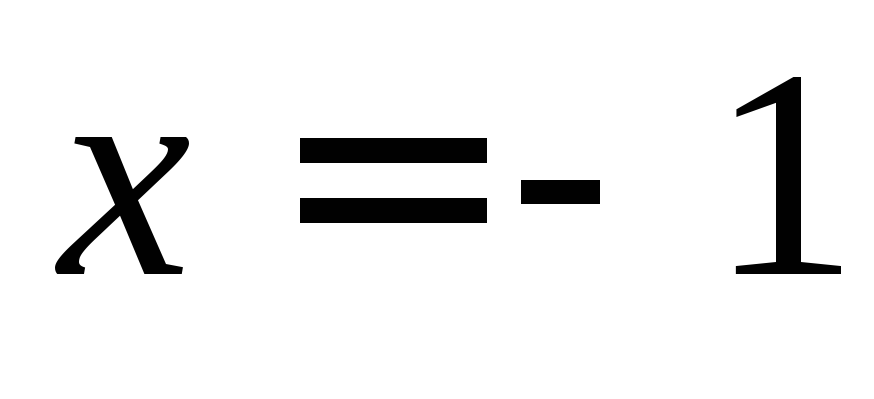 .
.Наклонная асимптота находится по формуле:
 .
Так
как
.
Так
как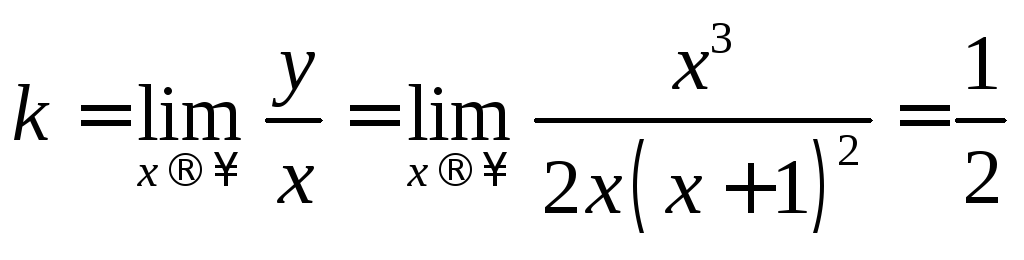 ;
;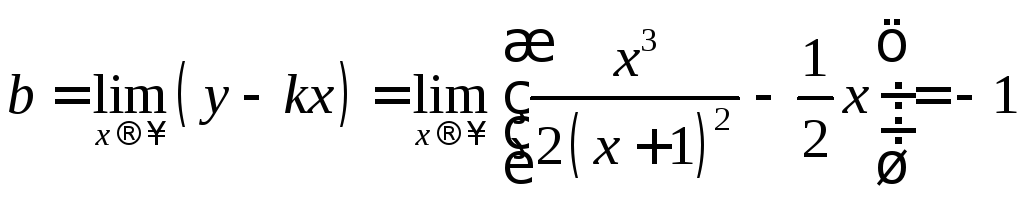 ,
то уравнение наклонной асимптоты
будет иметь вид:
,
то уравнение наклонной асимптоты
будет иметь вид: 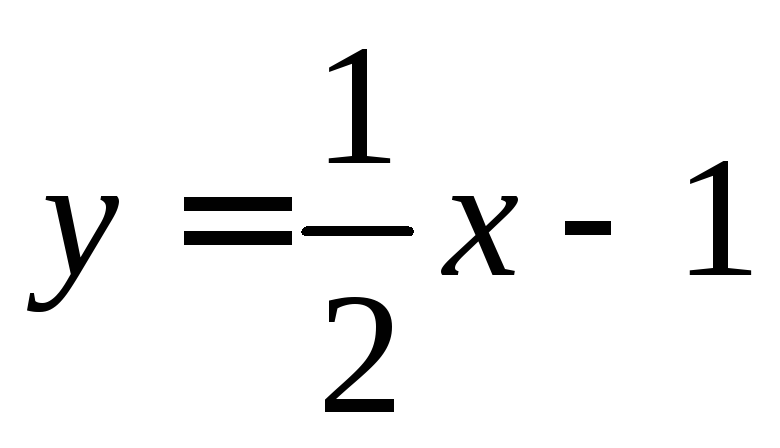 .
.Горизонтальных асимптот нет, так как
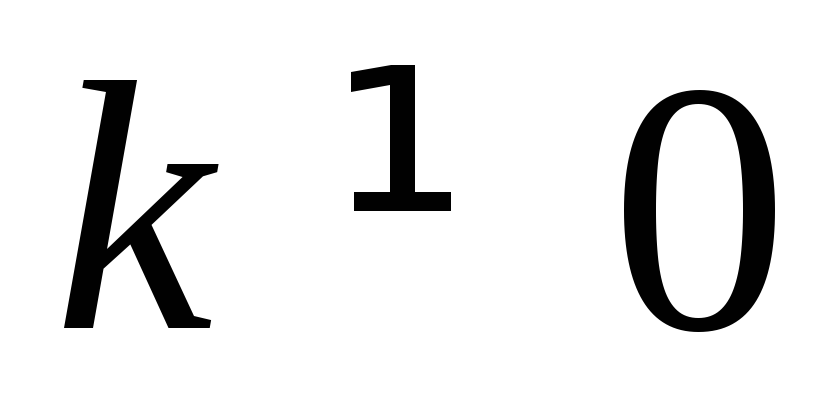 .
.
Найдем экстремумы функции:
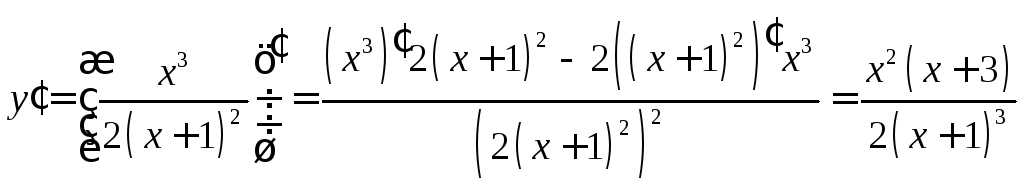 ,
значит
,
значит ![]() ,
, ![]() и
и ![]() — стационарные точки I
рода.
— стационарные точки I
рода.
![]() —точка
локального максимума, и
—точка
локального максимума, и ![]() ,
а точке
,
а точке![]() экстремума нет, так как в ней функция
терпит разрыв. Смотрите рис. 6.
экстремума нет, так как в ней функция
терпит разрыв. Смотрите рис. 6.
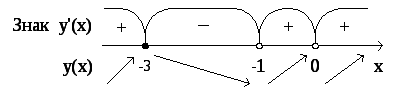
Рис. 6.
Найдём точки перегиба:
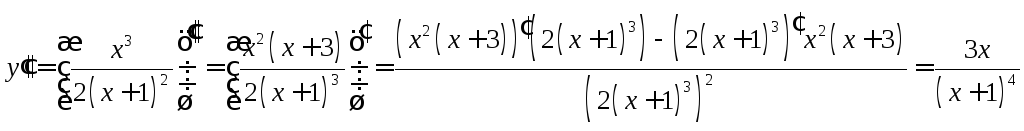 ,
значит
,
значит ![]() и
и ![]() — стационарные II
рода.
— стационарные II
рода.
В
точке ![]() функция
имеет перегиб. Ордината точки перегиба
—
функция
имеет перегиб. Ордината точки перегиба
—![]() .Смотрите
рис. 7.
.Смотрите
рис. 7.
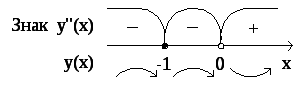
Рис. 7.
Сведём в таблицу все результаты проведённого исследования.
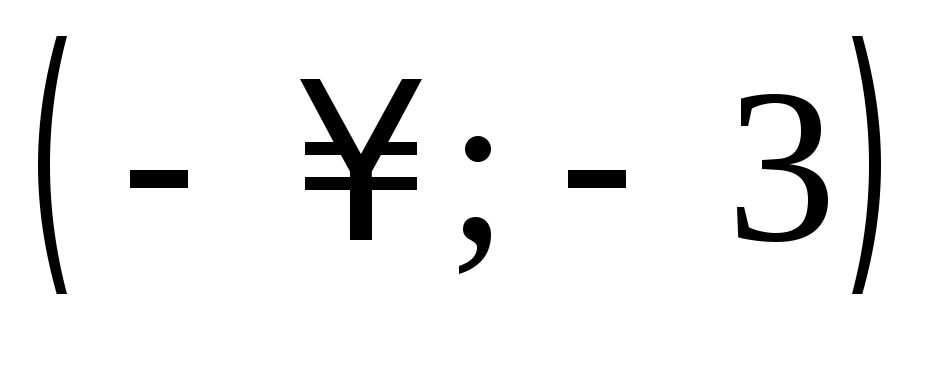
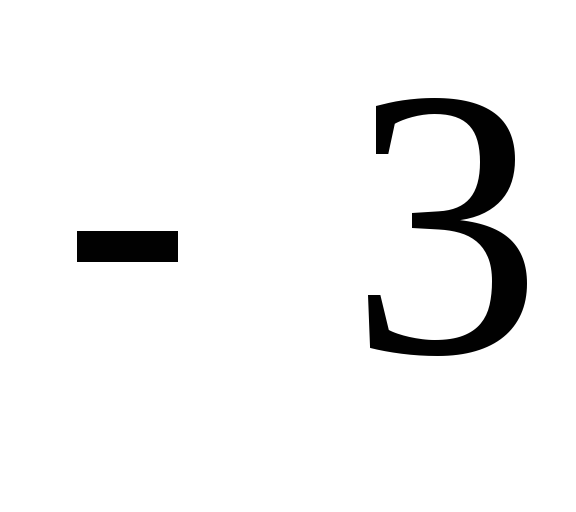
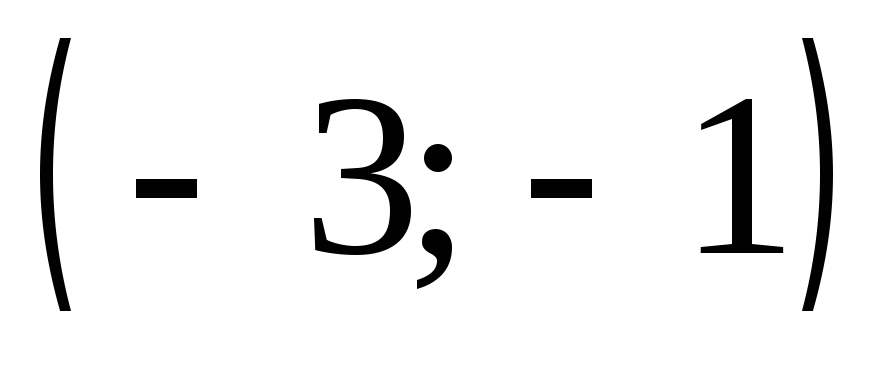
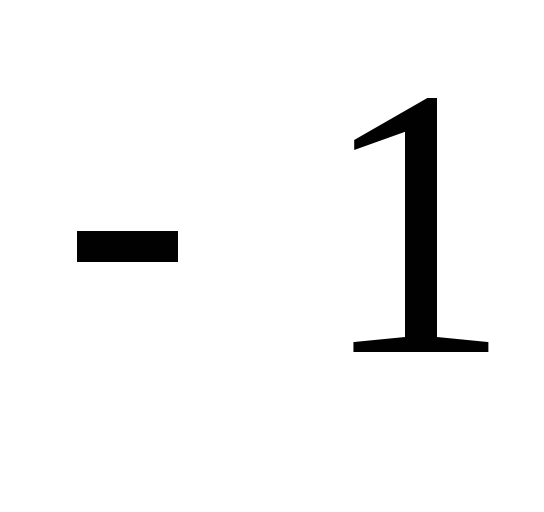
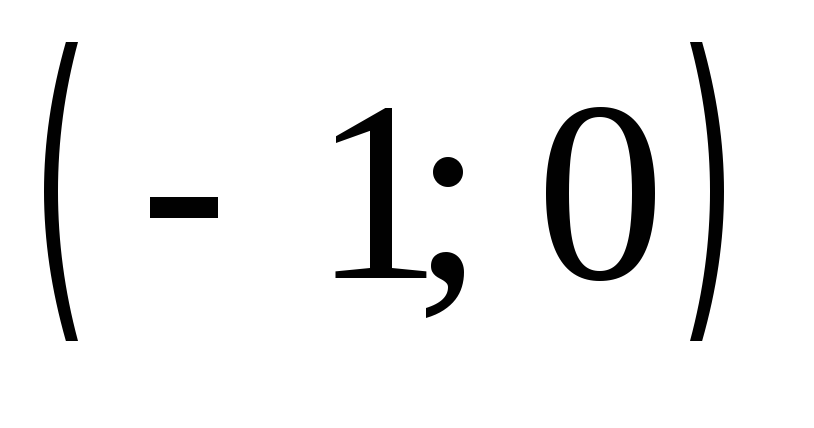
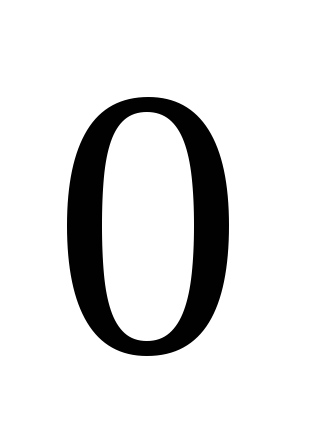
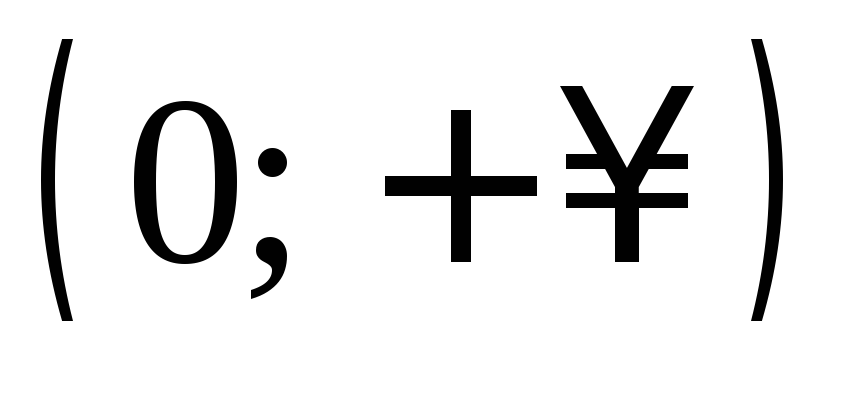
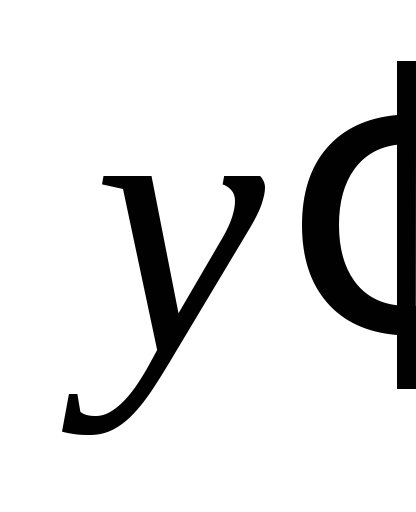





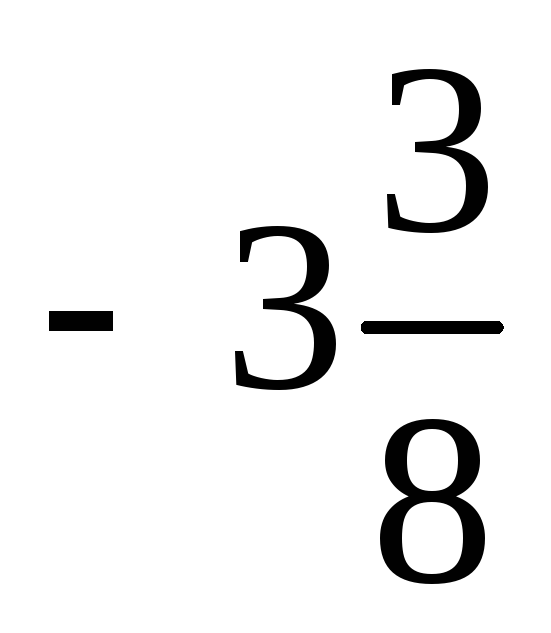
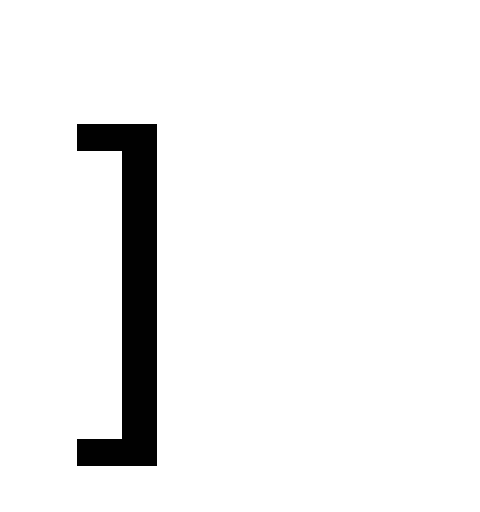

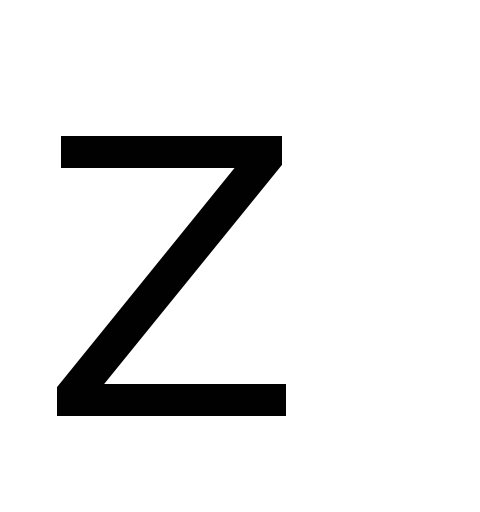
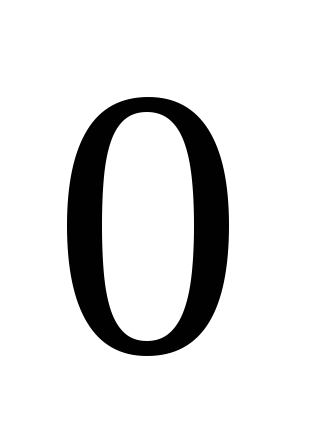
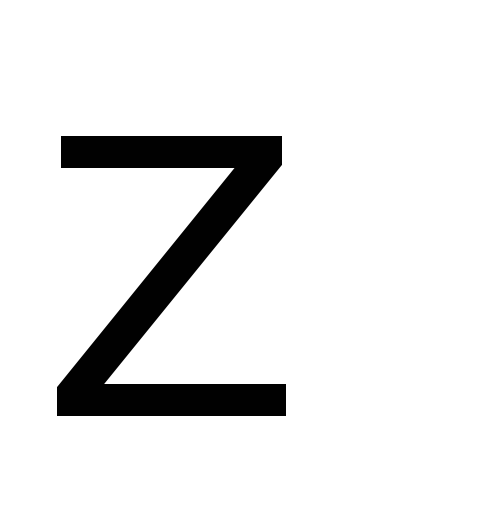




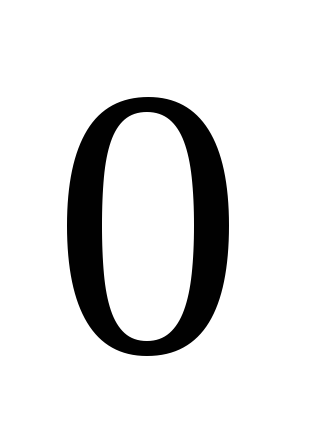
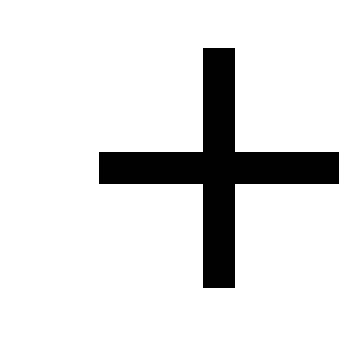

Точка разрыва
Точка перегиба



График данной функции представлен на рис. 8.
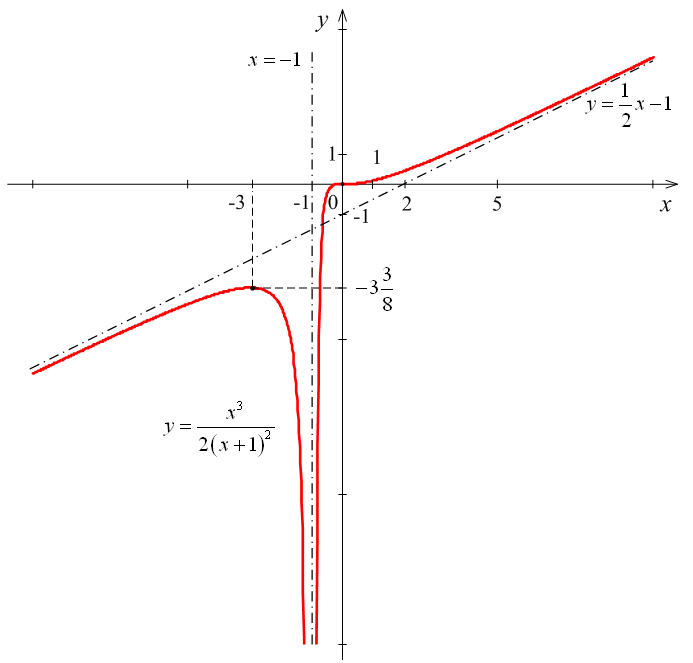
Рис. 8.
Задание
27. Найти
наименьшее и наибольше значения функции
![]() на отрезке
на отрезке![]() .
.
Решение:
![]()
![]() .
Имеем
.
Имеем![]() ,
так как
,
так как![]() .
.
![]()
![]() для
поиска экстремумов необходимо найти:
для
поиска экстремумов необходимо найти:
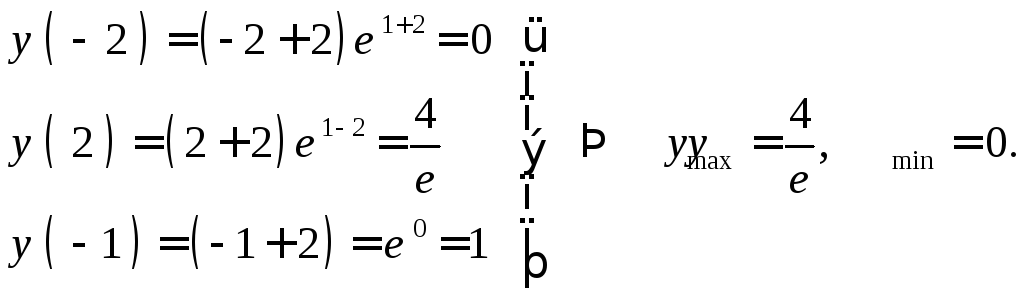
Задание
28. Найти
неопределенный интеграл ![]() .
.
Решение:
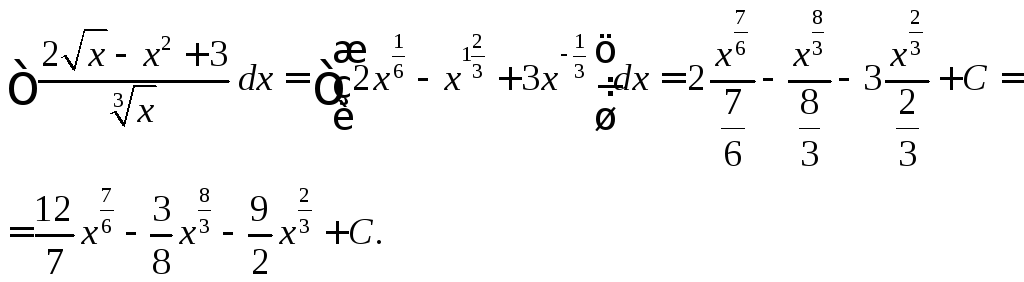
Задание
29. Найти
неопределенный интеграл ![]() .
.
Решение:
Воспользуемся методом замены:
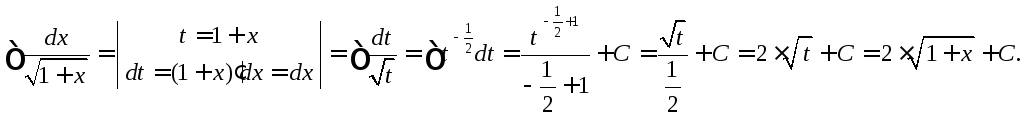
Задание
30. Найти
неопределенный интеграл ![]() .
.
Решение:
![]() .
.
Заметим,
что приведенное решение наглядно
демонстрирует метод замены, но слишком
«громоздко». Запись решения можно
упростить, если воспользоваться
очевидным выражением![]() .
С помощью этого равенства можно
«заносить» необходимый множитель под
знак дифференциала (См. Приложение).
.
С помощью этого равенства можно
«заносить» необходимый множитель под
знак дифференциала (См. Приложение).
Продемонстрируем эту идею на примере:
![]()
Задание
31. Найти
неопределенный интеграл![]() .
.
Решение:
![]() .
.
Задание
32. Найти
неопределенный интеграл ![]() .
.
Решение:
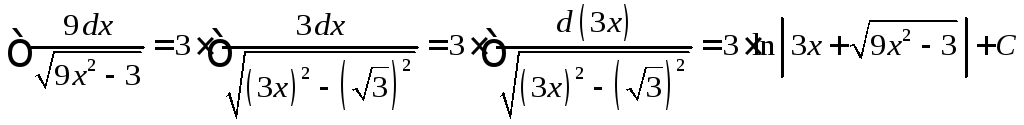 .
.
Задание
33. Найти
неопределенный интеграл ![]() .
.
Решение:
 .
.
Задание
34. Найти
неопределенный интеграл ![]() .
.
Решение:
Заметим,
что
![]() ,
следовательно,
,
следовательно,
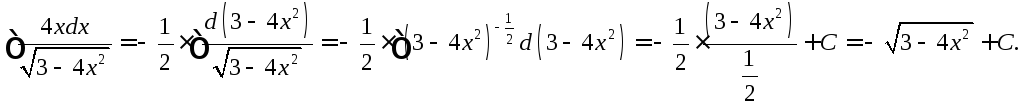
Задание
35. Найти
неопределенный интеграл ![]() .
.
Решение:
![]() .
.
Задание
36. Найти
неопределенный интеграл 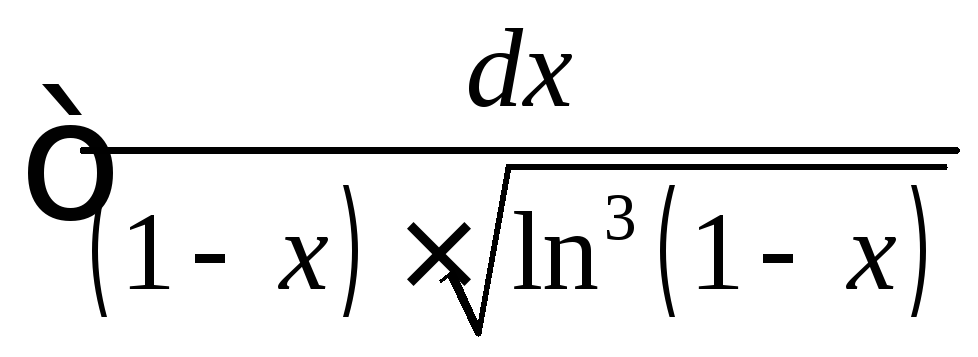 .
.
Решение:
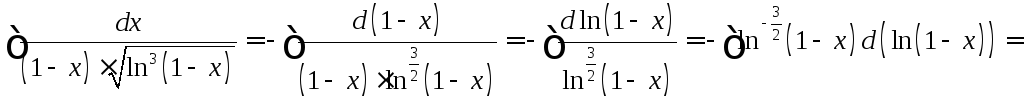
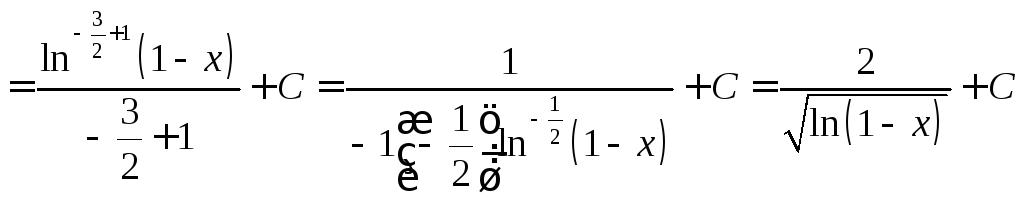 .
.
Задание
37. Найти
неопределенный интеграл ![]() .
.
Решение:
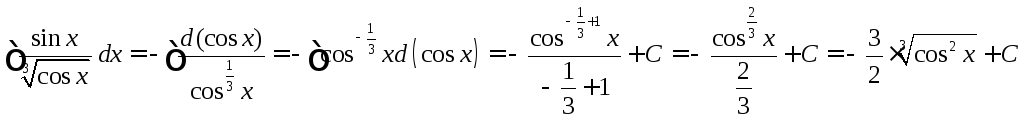 .
.
Задание
38. Найти
неопределенный интеграл ![]() .
.
Решение:
![]()
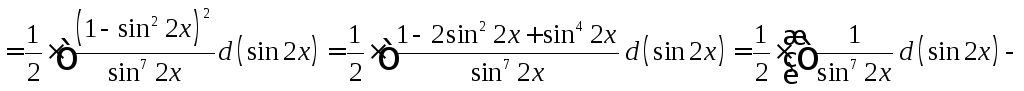
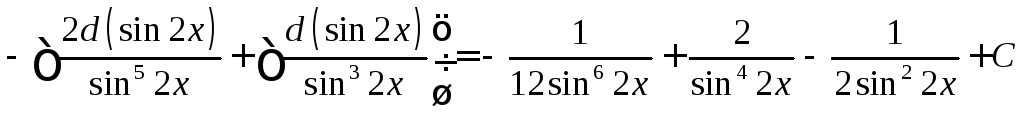
Задание
39. Найти
неопределенный интеграл ![]() .
.
Решение:
![]()
![]() .
.
Задание
40. Найти
неопределенный интеграл ![]() .
.
Решение:
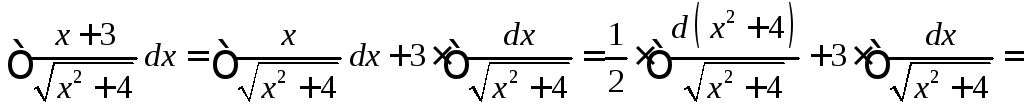
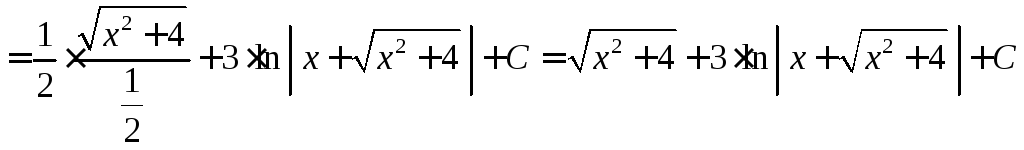 .
.
Задание
41. Найти
неопределенный интеграл ![]() .
.
Решение:
![]()
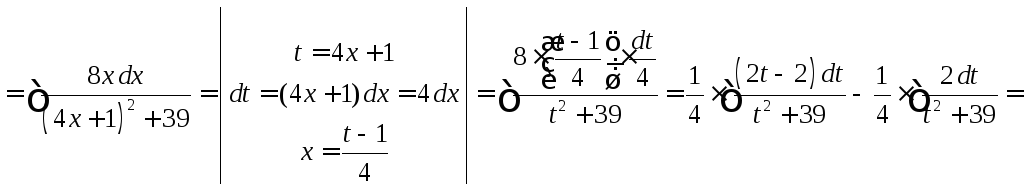
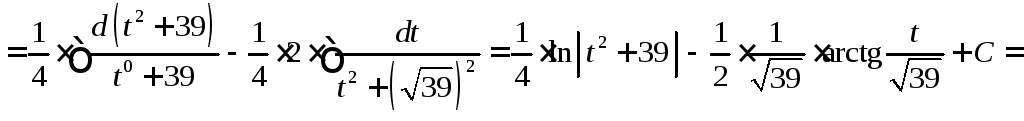
![]() .
.
Задание
42. Найти
неопределенный интеграл ![]() .
.
Решение:
![]() .
.
Задание
43. Найти
неопределенный интеграл ![]() .
.
Решение:
Преобразуем дробь, стоящую под знаком интеграла — выделим у неё целую часть, поделив числитель на знаменатель «уголком»:
|
_
|
|
|
|
|
|
|
|
| ||
|
_
|
|
|
|
|
|
|
|
|
|
|
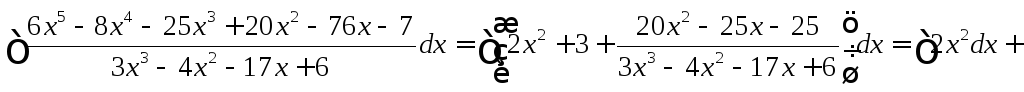
![]() .
.
Далее разложим
знаменатель полученной дроби на
множители. Для этого будем искать
возможные корни знаменателя методом
подбора среди делителей свободного
члена. Очевидно, что таким корнем будет
![]() ,
т. к. при
,
т. к. при![]() знаменатель данной дроби обращается
в ноль. Поделим знаменатель на
знаменатель данной дроби обращается
в ноль. Поделим знаменатель на![]() :
:
|
_
|
|
|
|
|
|
|
|
| ||
|
_
|
|
|
|
|
|
|
|
_
|
|
|
|
|
|
|
|
|
|
|
Таким образом,![]() и тогда
и тогда
![]() .
.
![]() .
.
Для того, чтобы
избежать при нахождении неопределенных
коэффициентов раскрытия скобок,
группировки и решения системы уравнений,
которая в некоторых случаях может
оказаться достаточно громоздкой,
применяют, так называемый,«метод
произвольных значений», суть которого
состоит в том, что в полученное выше
выражение подставляются поочередно
несколько (по числу неопределенных
коэффициентов) произвольных значений
![]() .
Для упрощения вычислений в качестве
произвольных значений принято принимать
точки, при которых знаменатель дроби
равен нулю, т.е. в нашем случае —
.
Для упрощения вычислений в качестве
произвольных значений принято принимать
точки, при которых знаменатель дроби
равен нулю, т.е. в нашем случае —![]() ,
,![]() и
и![]() .
.
В итоге получим
следующую систему уравнений: 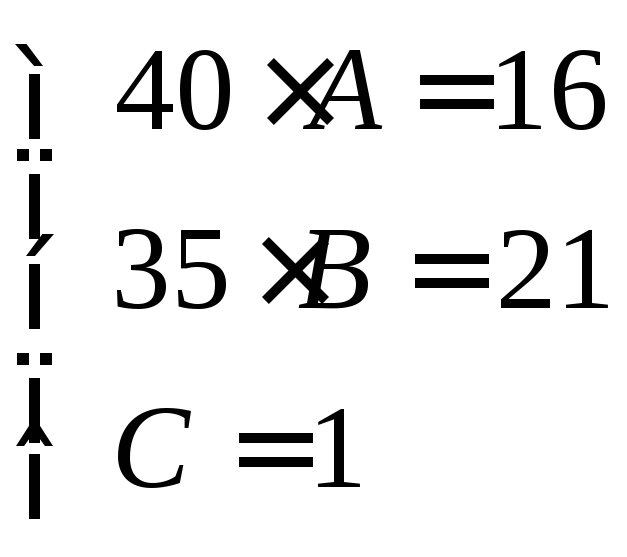 .
.
Корнями этой системы
будут: ![]() ,
,![]() , и
, и![]() .
.
Окончательно
получаем, что ![]()
![]()
Задание
44. Найти
неопределенный интеграл ![]() .
.
Решение:
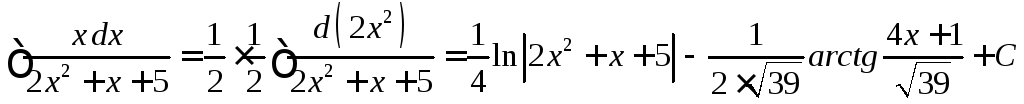 .
.
Задание
45. Вычислить
определенный интеграл 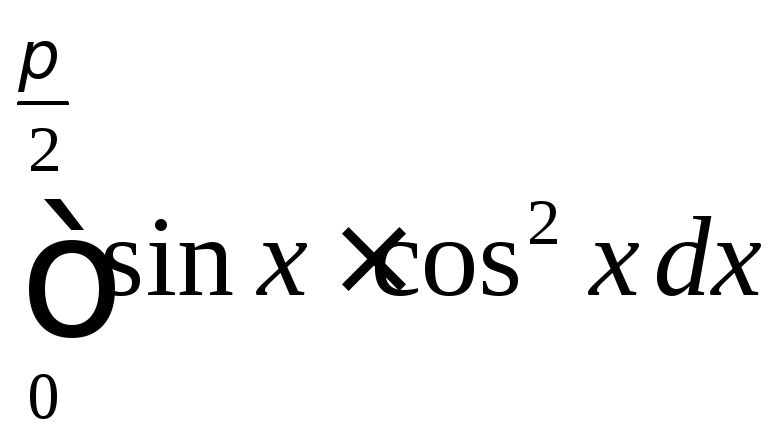 .
.
Решение:
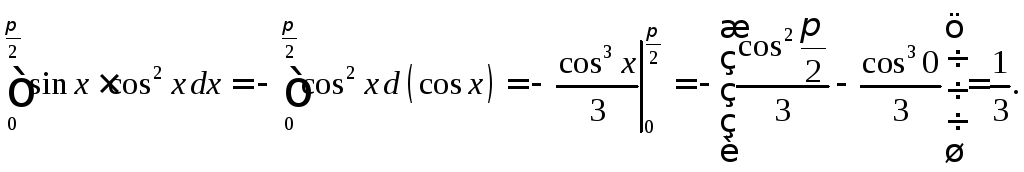
Задание
46. Вычислить
определенный интеграл ![]() .
.
Решение:
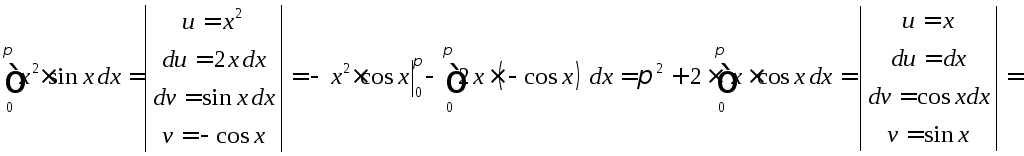
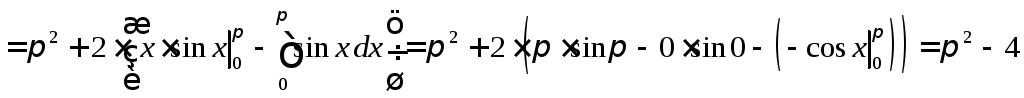 .
.
Задание
47. Найти
несобственный интеграл или доказать,
что он расходится: a) ![]() ; б)
; б) ![]() .
.
Решение:
![]() ,
т. е. данный интеграл расходится;
,
т. е. данный интеграл расходится;
![]() ,
значит данный интеграл сходится.
,
значит данный интеграл сходится.