
- •Найдите угол прямоугольного параллелепипеда, для которого , , . Ответ дайте в градусах.
- •Найдите угол прямоугольного параллелепипеда, для которого , , . Ответ дайте в градусах.
- •В правильной треугольной пирамиде — середина ребра , — вершина. Известно, что , а площадь боковой поверхности равна 3. Найдите длину отрезка .
- •В правильной треугольной пирамиде — середина ребра , — вершина. Известно, что , а площадь боковой поверхности равна 3. Найдите длину отрезка .
-
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
-
В сосуд, имеющий форму правильной треугольной призмы, налили 2300
 воды
и полностью в нее погрузили деталь. При
этом уровень жидкости в сосуде поднялся
с отметки 25 см до отметки 27 см. Чему
равен объем детали? Ответ выразите в
воды
и полностью в нее погрузили деталь. При
этом уровень жидкости в сосуде поднялся
с отметки 25 см до отметки 27 см. Чему
равен объем детали? Ответ выразите в
 .
.
-
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает
 см.
На какой высоте будет находиться уровень
воды, если ее перелить в другой такой
же сосуд, у которого сторона основания
в
см.
На какой высоте будет находиться уровень
воды, если ее перелить в другой такой
же сосуд, у которого сторона основания
в
 раза
больше, чем у первого? Ответ выразите
в см.
раза
больше, чем у первого? Ответ выразите
в см.
-
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны
 .
Найдите объем цилиндра, описанного
около этой призмы.
.
Найдите объем цилиндра, описанного
около этой призмы.
-
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны
 .
Найдите объем цилиндра, описанного
около этой призмы.
.
Найдите объем цилиндра, описанного
около этой призмы.
-
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
-
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
-
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
-
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
-
Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
-
В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
-
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
-
В цилиндрическом сосуде уровень жидкости достигает 8 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
-
В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 3 раза больше диаметра первого? Ответ выразите в сантиметрах
-
В цилиндрическом сосуде уровень жидкости достигает 48 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
-
В цилиндрическом сосуде уровень жидкости достигает 32 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
-
В цилиндрический сосуд налили
 воды.
Уровень жидкости оказался равным 12 см.
В воду полностью погрузили деталь. При
этом уровень жидкости в сосуде поднялся
на 9 см. Чему равен объем детали? Ответ
выразите в
воды.
Уровень жидкости оказался равным 12 см.
В воду полностью погрузили деталь. При
этом уровень жидкости в сосуде поднялся
на 9 см. Чему равен объем детали? Ответ
выразите в
 .
. -
В цилиндрический сосуд налили
 воды.
Уровень жидкости оказался равным 12 см.
В воду полностью погрузили деталь. При
этом уровень жидкости в сосуде поднялся
на 10 см. Чему равен объем детали? Ответ
выразите в
воды.
Уровень жидкости оказался равным 12 см.
В воду полностью погрузили деталь. При
этом уровень жидкости в сосуде поднялся
на 10 см. Чему равен объем детали? Ответ
выразите в  .
. -
В цилиндрический сосуд налили
 воды.
Уровень жидкости оказался равным 12 см.
В воду полностью погрузили деталь. При
этом уровень жидкости в сосуде поднялся
на 2 см. Чему равен объем детали? Ответ
выразите в
воды.
Уровень жидкости оказался равным 12 см.
В воду полностью погрузили деталь. При
этом уровень жидкости в сосуде поднялся
на 2 см. Чему равен объем детали? Ответ
выразите в
 .
.
-
В правильной шестиугольной призме
 все
ребра равны
все
ребра равны
 .
Найдите расстояние между точками
.
Найдите расстояние между точками
 и
и
 .
.
-
В правильной шестиугольной призме
 все
ребра равны 1. Найдите расстояние между
точками
все
ребра равны 1. Найдите расстояние между
точками
 и
и
 .
.
-
Найдите угол
 прямоугольного
параллелепипеда, для которого
прямоугольного
параллелепипеда, для которого
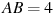 ,
,
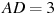 ,
,
 .
Ответ дайте в градусах.
.
Ответ дайте в градусах.
-
Найдите угол прямоугольного параллелепипеда, для которого , , . Ответ дайте в градусах.
-
Найдите угол прямоугольного параллелепипеда, для которого , , . Ответ дайте в градусах.
-
Найдите расстояние между вершинами
 и
и
 прямоугольного
параллелепипеда, для которого
прямоугольного
параллелепипеда, для которого
 ,
,
 ,
,
 .
.
-
В правильной треугольной пирамиде
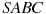
 —
середина ребра
—
середина ребра
 ,
,
 —
вершина. Известно, что
—
вершина. Известно, что
 ,
а площадь боковой поверхности равна
3. Найдите длину отрезка
,
а площадь боковой поверхности равна
3. Найдите длину отрезка
 .
.
-
В правильной треугольной пирамиде — середина ребра , — вершина. Известно, что , а площадь боковой поверхности равна 3. Найдите длину отрезка .
-
В правильной треугольной пирамиде
 медианы
основания пересекаются в точке
медианы
основания пересекаются в точке
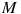 .
Площадь треугольника
.
Площадь треугольника
 равна
3, объем пирамиды равен 1. Найдите длину
отрезка
равна
3, объем пирамиды равен 1. Найдите длину
отрезка
 .
.
-
Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.
-
Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.
-
Диаметр основания конуса равен 6, а длина образующей — 5. Найдите высоту конуса.
-
Площадь боковой поверхности цилиндра равна
 ,
а диаметр основания — 1. Найдите
высоту цилиндра.
,
а диаметр основания — 1. Найдите
высоту цилиндра.
-
В правильной четырехугольной пирамиде
 точка
точка
 —
центр основания,
—
центр основания,
 вершина,
вершина,
 ,
,
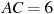 .
Найдите длину отрезка
.
Найдите длину отрезка
 .
.
-
В правильной четырехугольной пирамиде
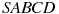 точка
точка
 —
центр основания,
—
центр основания,
 вершина,
вершина,
 ,
,
 .
Найдите длину отрезка
.
Найдите длину отрезка
 .
.
-
В правильной треугольной пирамиде

 —
середина ребра
—
середина ребра
 ,
,
 —
вершина. Известно, что
—
вершина. Известно, что
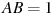 ,
а
,
а
 .
Найдите площадь боковой поверхности.
.
Найдите площадь боковой поверхности.
-
В правильной треугольной пирамиде — середина ребра , — вершина. Известно, что , а площадь боковой поверхности равна 3. Найдите длину отрезка .
-
В правильной треугольной пирамиде

 —
середина ребра
—
середина ребра
 ,
,
 —
вершина. Известно, что
—
вершина. Известно, что
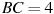 ,
а
,
а
 .
Найдите площадь боковой поверхности.
.
Найдите площадь боковой поверхности. -
Найдите площадь фигуры, ограниченной линиями

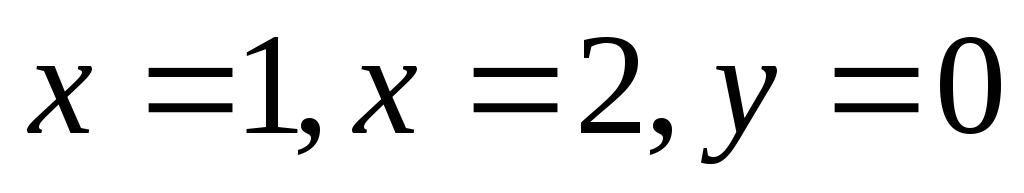
-
Найдите площадь фигуры, ограниченной линиями
-
 ,
,
 ,
,
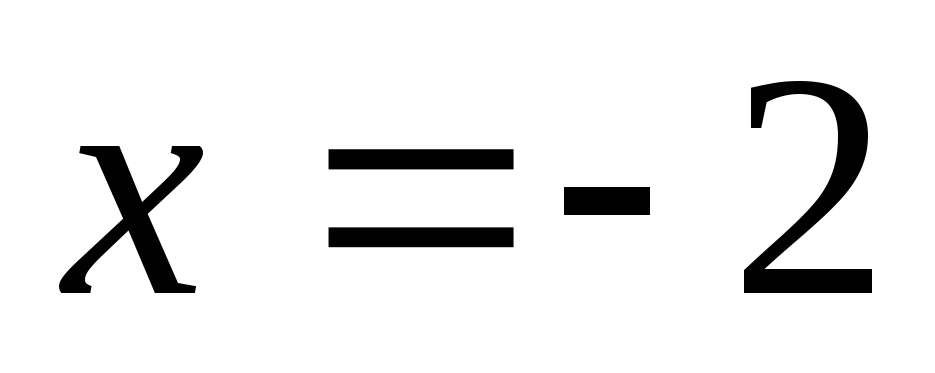 ,
,

-
Найдите площадь фигуры, ограниченной линиями
 ,
,

-
Найдите площадь фигуры, ограниченной линиями
 ,
,

-
Найдите площадь фигуры, ограниченной линиями
-
 ,
,
 ,
,
 ,
,

-
Найдите площадь фигуры, ограниченной линиями
-
 ,
,
 ,
,
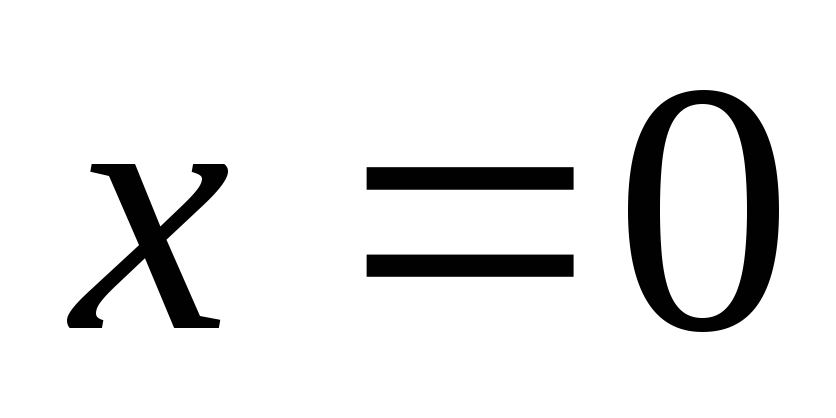 ,
,

-
Найдите площадь фигуры, ограниченной линиями
-
 ,
,
 ,
,
 ,
,

-
Найдите площадь фигуры, ограниченной линиями
-
 ,
,
 ,
,
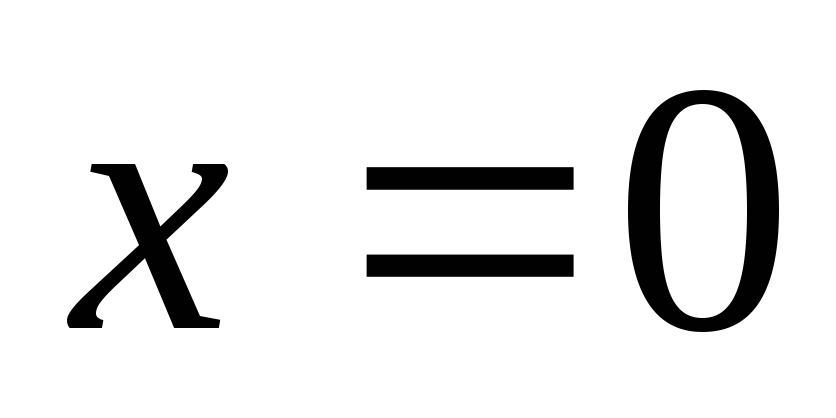 ,
,

-
Найдите площадь фигуры, ограниченной линиями
-
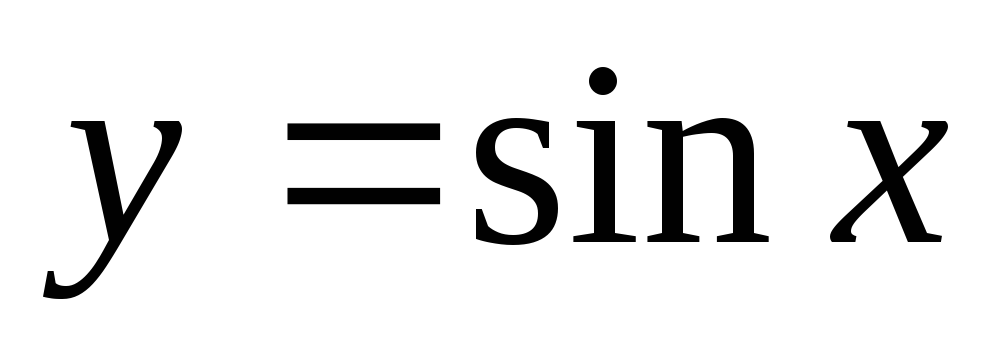 ,
,
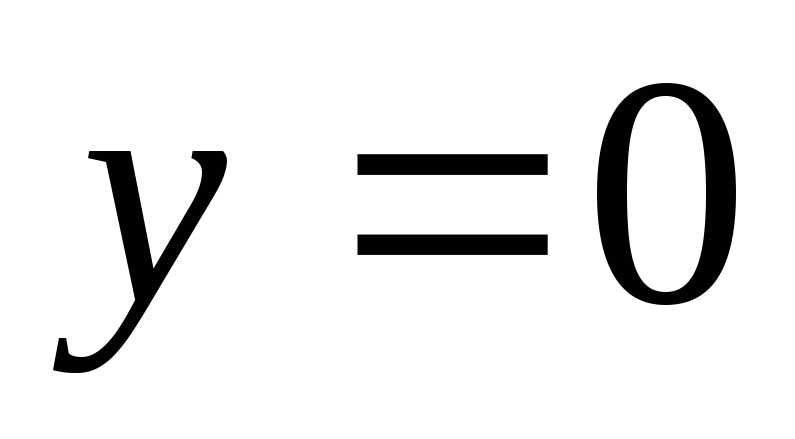 ,
,
 ,
,

-
Найдите площадь фигуры, ограниченной линиями
-
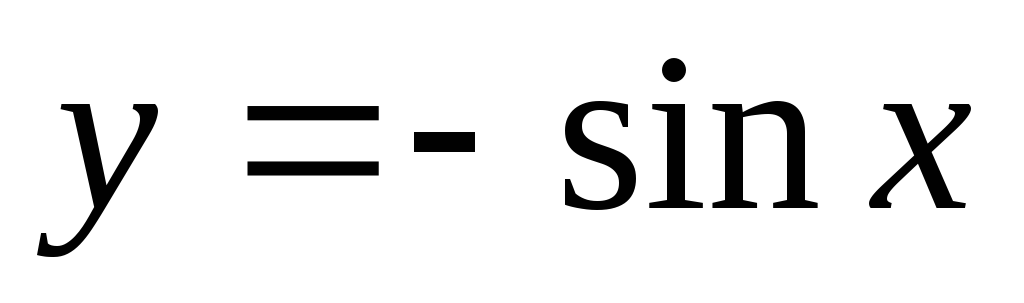 ,
,
 ,
,
 ,
,

-
Найдите площадь фигуры, ограниченной линиями
-
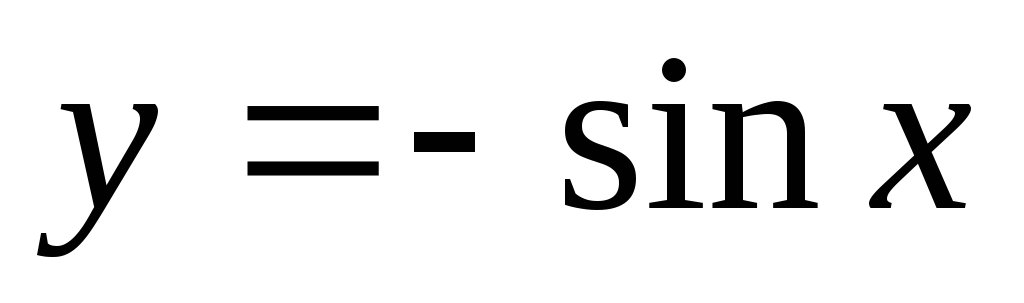 ,
,
 ,
,
 ,
,

-
Найдите площадь фигуры, ограниченной линиями
-
 ,
,
 ,
,
 ,
,

-
Найдите площадь фигуры, ограниченной линиями
-
 ,
,
 ,
,
 ,
,
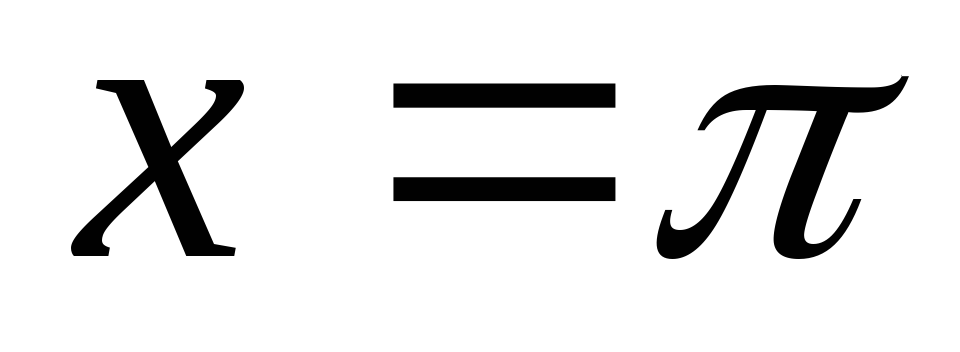
-
Найдите площадь фигуры, ограниченной линиями
-
 ,
,
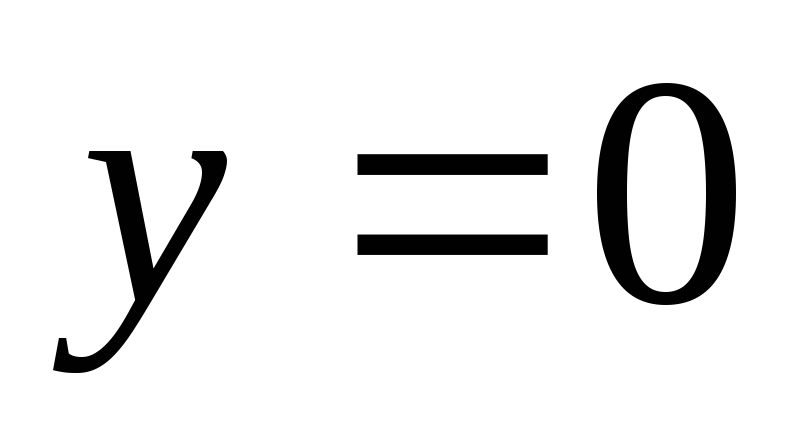 ,
,
 ,
,

-
Вычислите интеграл

-
Вычислите интеграл

-
Вычислите интеграл

-
Вычислите интеграл
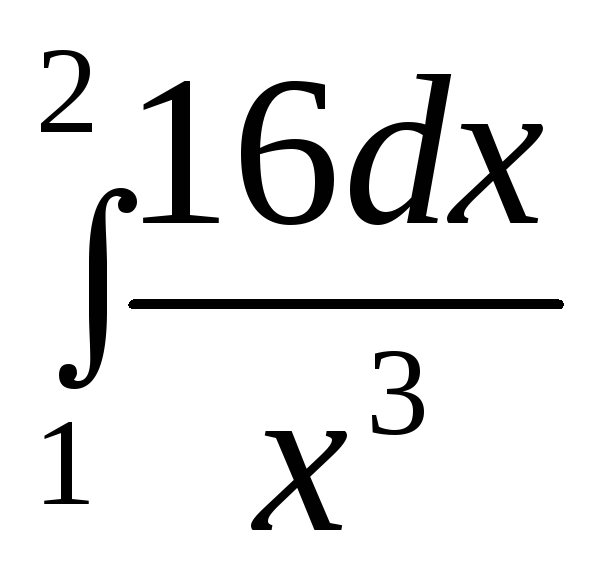
-
Вычислите интеграл
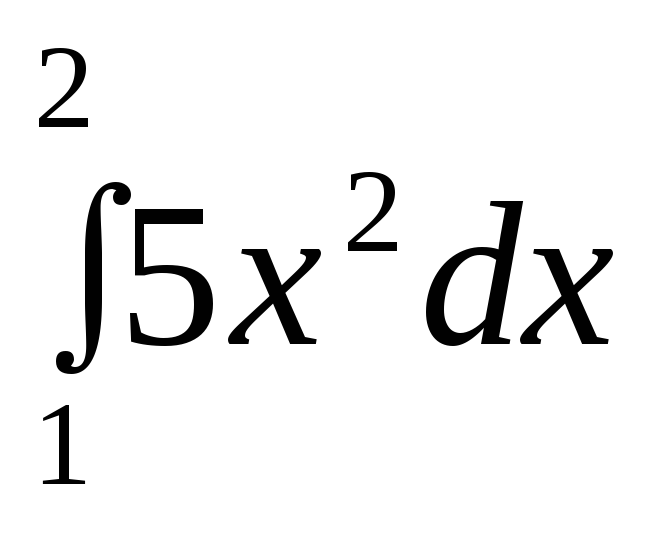
-
Вычислите интеграл
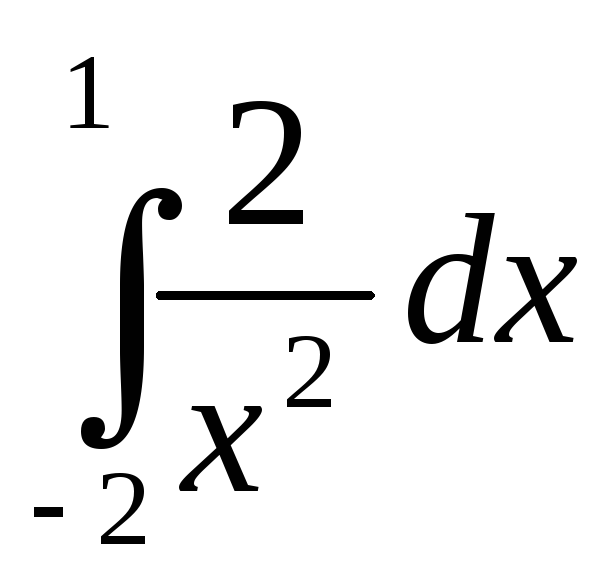
-
Вычислите интеграл

-
Вычислите интеграл

-
Вычислите интеграл

-
Вычислите интеграл

-
Вычислите интеграл

-
Вычислите интеграл
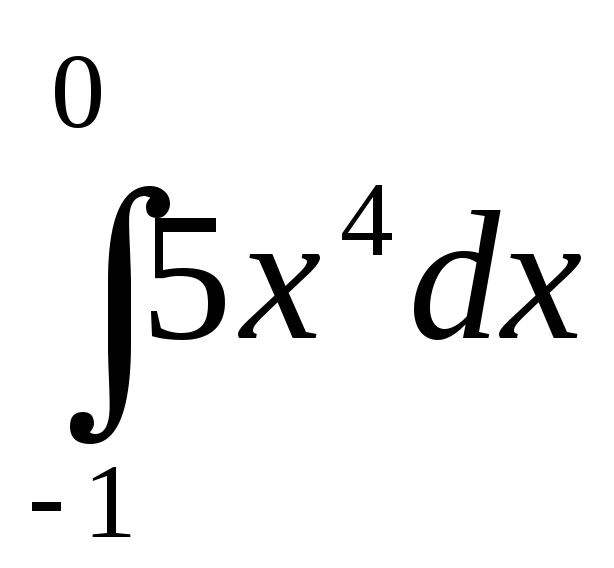
-
Вычислите интеграл

-
Вычислите интеграл

-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с. -
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с. -
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с. -
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с. -
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
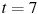 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
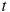 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
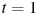 с.
с. -
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с. -
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с. -
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
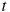 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
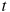 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с. -
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с.
-
Материальная точка движется прямолинейно по закону
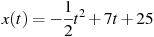 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
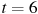 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
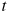 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
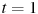 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
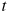 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с.
-
Материальная точка движется прямолинейно по закону
 ,
где
,
где
 —
расстояние от точки отсчета в метрах,
—
расстояние от точки отсчета в метрах,
 —
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
—
время в секундах, измеренное с начала
движения. Найдите ее скорость (в метрах
в секунду) в момент времени
 с.
с.
-
Прямая
 является
касательной к графику функции
является
касательной к графику функции
 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания.
-
Прямая
 является
касательной к графику функции
является
касательной к графику функции
 .
Найдите b, учитывая, что абсцисса
точки касания больше 0.
.
Найдите b, учитывая, что абсцисса
точки касания больше 0.
-
Прямая
 параллельна
касательной к графику функции
параллельна
касательной к графику функции
 .
Найдите абсциссу точки касания
.
Найдите абсциссу точки касания
-
Прямая
 параллельна
касательной к графику функции
параллельна
касательной к графику функции
 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания.
-
Прямая
 параллельна
касательной к графику функции
параллельна
касательной к графику функции
 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания.
-
Прямая
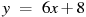 параллельна
касательной к графику функции
параллельна
касательной к графику функции
 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания.
-
Прямая
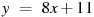 параллельна
касательной к графику функции
параллельна
касательной к графику функции
 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания.
-
Прямая
 параллельна
касательной к графику функции
параллельна
касательной к графику функции
 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания.
-
Прямая
 параллельна
касательной к графику функции
параллельна
касательной к графику функции
 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания. -
Прямая
 параллельна
касательной к графику функции
параллельна
касательной к графику функции
 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания. -
Прямая
 параллельна
касательной к графику функции
параллельна
касательной к графику функции
 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания. -
Прямая
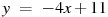 параллельна
касательной к графику функции
параллельна
касательной к графику функции
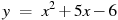 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания. -
Прямая
 параллельна
касательной к графику функции
параллельна
касательной к графику функции
 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания. -
Прямая
 параллельна
касательной к графику функции
параллельна
касательной к графику функции
 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания. -
Прямая
 параллельна
касательной к графику функции
параллельна
касательной к графику функции
 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания. -
Прямая
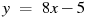 параллельна
касательной к графику функции
параллельна
касательной к графику функции
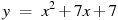 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания. -
Прямая
 параллельна
касательной к графику функции
параллельна
касательной к графику функции
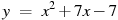 .
Найдите абсциссу точки касания.
.
Найдите абсциссу точки касания.
-
Найдите наибольшее значение функции
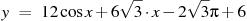 на
отрезке
на
отрезке

-
Найдите наименьшее значение функции
 на
отрезке
на
отрезке
 .
.
-
Найдите наибольшее значение функции
 на
отрезке
на
отрезке
 .
.
-
Найдите наименьшее значение функции
 на
отрезке
на
отрезке
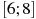 .
. -
Найдите наименьшее значение функции
 на
отрезке
на
отрезке
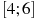
-
Найдите наименьшее значение функции
 на
отрезке
на
отрезке
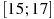
-
Найдите наименьшее значение функции
 на
отрезке
на
отрезке
 .
. -
Найдите наибольшее значение функции
 на
отрезке
на
отрезке
 .
. -
Найдите наибольшее значение функции
 на
отрезке
на
отрезке
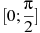 .
. -
Найдите наибольшее значение функции
 на
отрезке
на
отрезке

-
Найдите наибольшее значение функции
 на
отрезке
на
отрезке
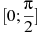
-
Найдите наименьшее значение функции
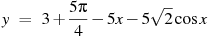 на
отрезке
на
отрезке
 .
. -
Найдите наименьшее значение функции
 на
отрезке
на
отрезке
 .
. -
Найдите наибольшее значение функции
 на
отрезке
на
отрезке
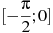
-
Найдите точку максимума функции

-
Найдите точку минимума функции

-
Найдите наименьшее значение функции
 на
отрезке
на
отрезке

-
Найдите наибольшее значение функции
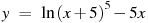 на
отрезке
на
отрезке
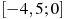 .
.
-
Научная конференция проводится в 3 дня. Всего запланировано 40 докладов — в первый день 16 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 15 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Научная конференция проводится в 3 дня. Всего запланировано 75 докладов — в первый день 27 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Научная конференция проводится в 4 дня. Всего запланировано 50 докладов — первые два дня по 11 докладов, остальные распределены поровну между третьим и четвертым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Научная конференция проводится в 3 дня. Всего запланировано 80 докладов — в первый день 16 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Научная конференция проводится в 3 дня. Всего запланировано 75 докладов — в первый день 21 доклад, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Научная конференция проводится в 4 дня. Всего запланировано 80 докладов — первые два дня по 30 докладов, остальные распределены поровну между третьим и четвертым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Научная конференция проводится в 4 дня. Всего запланировано 80 докладов — первые два дня по 32 доклада, остальные распределены поровну между третьим и четвертым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Научная конференция проводится в 4 дня. Всего запланировано 60 докладов — первые два дня по 18 докладов, остальные распределены поровну между третьим и четвертым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Научная конференция проводится в 5 дней. Всего запланировано 80 докладов — первые три дня по 12 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Научная конференция проводится в 3 дня. Всего запланировано 40 докладов — в первый день 18 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Научная конференция проводится в 5 дней. Всего запланировано 50 докладов — первые три дня по 8 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Научная конференция проводится в 3 дня. Всего запланировано 70 докладов — в первый день 28 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Научная конференция проводится в 3 дня. Всего запланировано 40 докладов — в первый день 20 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
-
Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
-
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
-
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых.
-
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых.
-
Построить график функции
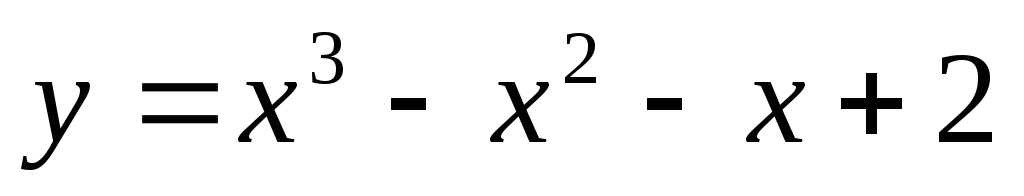 ,
на
,
на

-
Вычислить площадь фигуры, ограниченной линиями
 ,
y = 3
,
y = 3 -
Скорость движения тела изменяется по закону
 .
Найти путь, пройденный телом за 4 секунды
от начала движения.
.
Найти путь, пройденный телом за 4 секунды
от начала движения. -
Апофема правильной треугольной пирамиды равна 2а, высота пирамиды равна
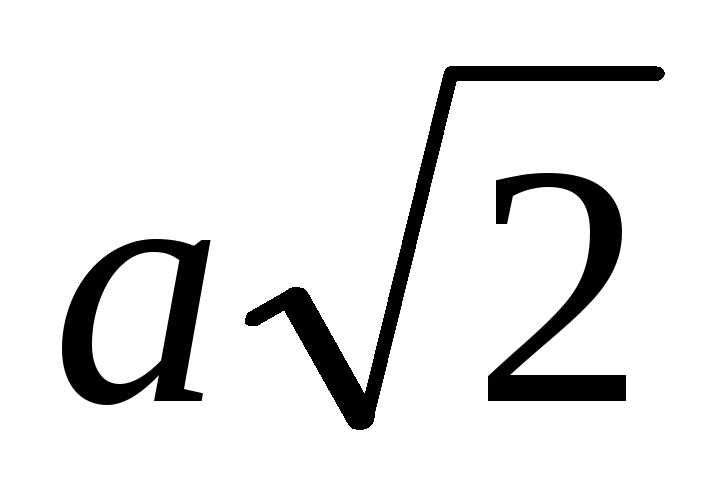 .
Найти сторону основания пирамиды, угол
между боковой гранью и основанием,
площадь поверхности пирамиды.
.
Найти сторону основания пирамиды, угол
между боковой гранью и основанием,
площадь поверхности пирамиды. -
Построить график функции
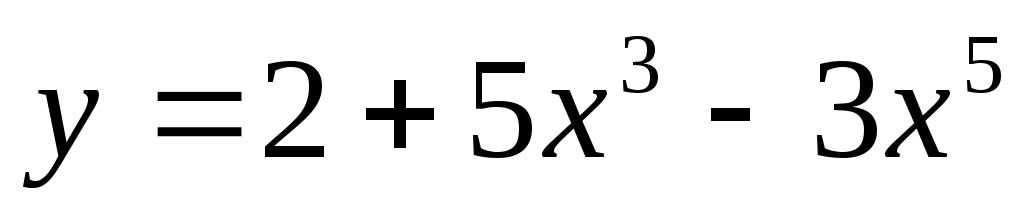
-
Вычислить площадь фигуры, ограниченной линиями
 ,
y = 3
,
y = 3 -
Тело брошено вертикально вверх со скоростью
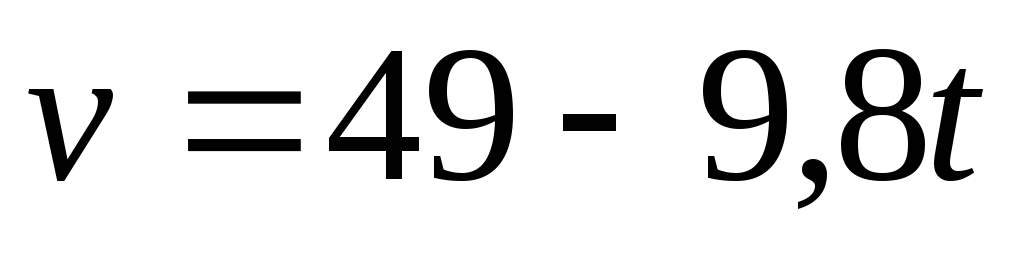 .
Найти наибольшую высоту подъема
.
Найти наибольшую высоту подъема
-
Высота правильной треугольной пирамиды равна
 ,
радиус окружности, описанной около
основания, 2а. Найти плоский угол при
вершине пирамиды.
,
радиус окружности, описанной около
основания, 2а. Найти плоский угол при
вершине пирамиды. -
Построить график функции

-
Вычислить площадь фигуры, ограниченной линиями
 и осью ОХ
и осью ОХ -
Скорость движения точки выражается формулой
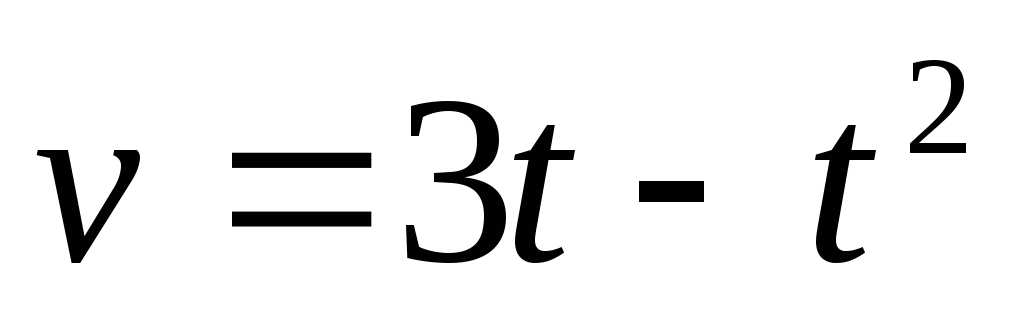 .
Найти путь, пройденный точкой от начала
движения до остановки.
.
Найти путь, пройденный точкой от начала
движения до остановки. -
Основание пирамиды - треугольник со сторонами 12,10, 10. Каждая боковая грань наклонена к плоскости основания под углом 45 . Найти площадь боковой поверхности пирамиды.
-
Построить график функции f (x) =
 на [0;16]
на [0;16] -
Вычислить площадь фигуры, ограниченной линиями y = x3 , y = 2x - x2 и осью OX
-
Скорость движения точки выражается формулой
 3
(м/с) Найти путь, пройденный точкой от
начала движении до остановки.
3
(м/с) Найти путь, пройденный точкой от
начала движении до остановки. -
Основанием пирамиды является треугольник со сторонами 12см,10см и 10см. Каждая боковая грань наклонена к основанию под углом 450. Найдите площадь боковой поверхности пирамиды
-
Построить график функции
 на [1;16]
на [1;16] -
Вычислить площадь фигуры, ограниченной линиями
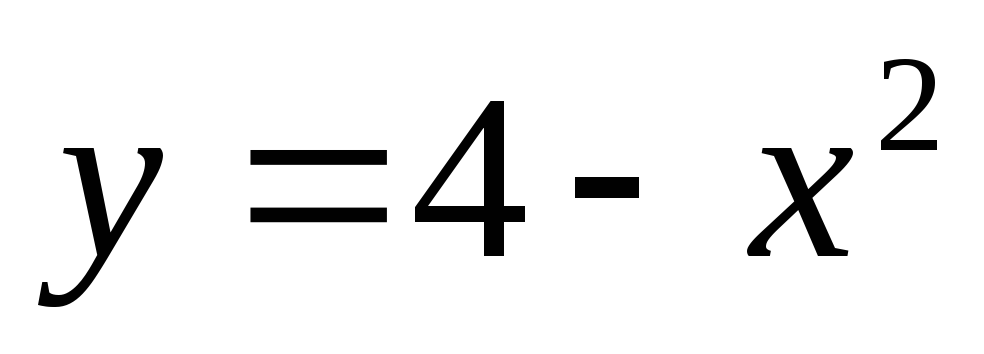 ,
,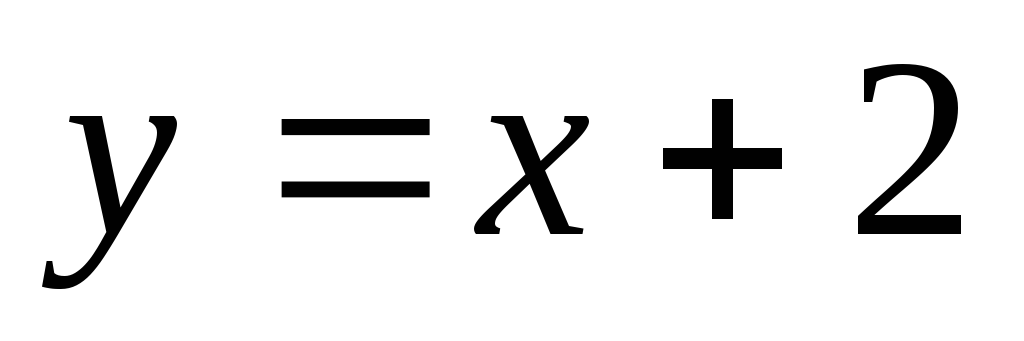 и осью 0X
и осью 0X
-
Найти путь, пройденный телом от начала движения до его остановки, если скорость прямолинейного движения изменяется по закону:
 (м/с)
(м/с) -
Основанием пирамиды ДАВС является треугольник АВС, у которого АВ=АС=13см, ВС= 10см, ребро АД перпендикулярно к плоскости основания и равно 9 см. Найти площадь боковой поверхности пирамиды
-
Построить график функции f(х) = 2+5х3-3х5
-
Вычислить площадь фигуры, ограниченной линиями у =3х2, у = 1,5х+4,5 и осью ох
-
Тело брошено вертикально вверх со скоростью V = 49-9,8t (м/с). Найти наибольшую высоту его подъема.
-
Высота правильной треугольной пирамиды а
 ,
радиус окружности, описанной около ее
основания, 2а. Найти плоский угол при
вершине пирамиды
,
радиус окружности, описанной около ее
основания, 2а. Найти плоский угол при
вершине пирамиды -
Построить график функции y = x 3-12x+4 на [-3;3]
-
Вычислить площадь фигуры, ограниченной линиями: y =1- x2 и y = x2-1
-
Тело брошено вертикально вверх со скоростью v(t)= 39,2 - 9,8t (м/с) Найти наибольшую высоту его подъема
-
Высота правильной пирамиды равна
 .
Высота ее боковой грани 2а. Найти
расстояние от центра основание пирамиды
до плоскости боковой грани.
.
Высота ее боковой грани 2а. Найти
расстояние от центра основание пирамиды
до плоскости боковой грани. -
Построить график функции f (x) = x3 – x2 - x +2 на [-1;2]
-
Вычислить площадь фигуры, ограниченной линиями y = 4- x2 и y = x+2
-
Скорость материальной точки задана формулой
 Найти путь пройденный точкой за первые
4 с после начала движения .
Найти путь пройденный точкой за первые
4 с после начала движения .
-
Основанием прямого параллелепипеда ABCDA, B,C,D, является ромб, ABCD, сторона которого равна
 и угол равен 60о. Плоскость AD,C,
составляет с плоскостью основания угол
60о Найти площадь боковой
поверхности.
и угол равен 60о. Плоскость AD,C,
составляет с плоскостью основания угол
60о Найти площадь боковой
поверхности.
-
Построить график функции
 на [-4; 2]
на [-4; 2]
-
Вычислить площадь фигуры, ограниченной линиями
 ,
х = 2, х =3 и у=0
,
х = 2, х =3 и у=0 -
Скорость движения тела задана уравнением
 .
Определить путь, пройденный телом от
начала движения до остановки.
.
Определить путь, пройденный телом от
начала движения до остановки.
-
Высота правильной треугольной пирамиды равна
 ,
радиус окружности, описанной около её
основания равен 2а. Найти площадь боковой
поверхности.
,
радиус окружности, описанной около её
основания равен 2а. Найти площадь боковой
поверхности. -
Построить график функции
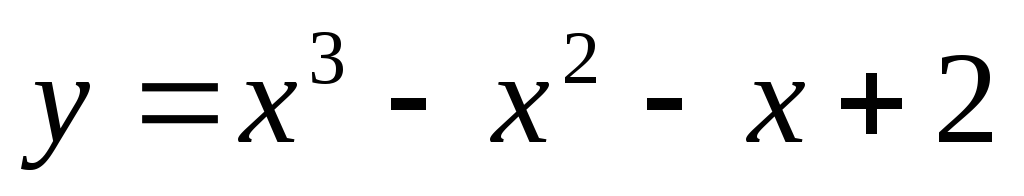 ,
на
,
на

